标签:
求积分的龙贝格算法
计算f(x)=1/x在[1,3]上的积分:
1 #include <iostream> 2 #include <cstring> 3 #include <cmath> 4 using namespace std; 5 6 double f(double x){ 7 return 1.0/x; 8 } 9 10 int main(){ 11 double a,b;//积分区间的上界和下届 12 a=1; 13 b=3; 14 15 double t[100]; 16 memset(t,-1,sizeof(t)); 17 t[1]=(b-a)/2.0*( f(a)+f(b) ) ; 18 for(int n=1;n<=8;n=2*n ) 19 { 20 double temp=0; 21 for(int i=0;i<=n-1;i++){ 22 temp+=f( a+(2*i+1)*(b-a)/(2*n) ); 23 } 24 temp=temp*(b-a)/(2*n); 25 t[2*n]=t[n]/2.0 + temp; 26 } 27 28 for(int i=1;i<=16;i=i*2){ 29 printf("t(%d)=%2.6f\n",i,t[i]); 30 } 31 printf("\n"); 32 33 double s[100]; 34 memset(s,-1,sizeof(s)); 35 for(int n=1;n<=8;n*=2) 36 { 37 s[n]=4.0/3.0*t[2*n]-t[n]/3.0; 38 } 39 for(int i=1;i<=8;i=i*2){ 40 printf("s(%d)=%2.6f\n",i,s[i]); 41 } 42 printf("\n"); 43 44 double c[100]; 45 memset(c,-1,sizeof(c)); 46 for(int n=1;n<=4;n*=2) 47 { 48 c[n]=16.0/15.0*s[2*n]-s[n]/15.0; 49 } 50 for(int i=1;i<=4;i=i*2){ 51 printf("c(%d)=%2.6f\n",i,c[i]); 52 } 53 printf("\n"); 54 55 double r[100]; 56 memset(r,-1,sizeof(r)); 57 for(int n=1;n<=2;n*=2) 58 { 59 r[n]=64.0/63.0*c[2*n]-c[n]/63.0; 60 } 61 for(int i=1;i<=2;i=i*2){ 62 printf("r(%d)=%2.8f\n",i,r[i]); 63 } 64 65 66 }
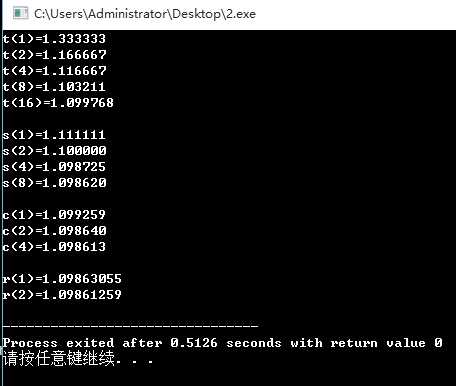
输出结果为:
标签:
原文地址:http://www.cnblogs.com/liugl7/p/4960706.html