标签:
部分转自 http://blog.csdn.net/whuslei/article/details/6442755
排序算法经过了很长时间的演变,产生了很多种不同的方法。对于初学者来说,对它们进行整理便于理解记忆显得很重要。每种算法都有它特定的使用场合,很难通用。因此,我们很有必要对所有常见的排序算法进行归纳。
我不喜欢死记硬背,我更偏向于弄清来龙去脉,理解性地记忆。比如下面这张图,我们将围绕这张图来思考几个问题。
上面的这张图来自一个PPT。它概括了数据结构中的所有常见的排序算法。现在有以下几个问题:
1、每个算法的思想是什么?
2、每个算法的稳定性怎样?时间复杂度是多少?
3、在什么情况下,算法出现最好情况 or 最坏情况?
4、每种算法的具体实现又是怎样的?
这个是排序算法里面最基本,也是最常考的问题。下面是我的小结。
一,冒泡排序:
1、简介:冒泡排序是最简单的排序,是刚学c语言时最早接触到的一个算法。
他的思想就是,对待排序元素的关键字从后往前进行多遍扫描,遇到相邻两个关键字次序与排序规则不符时,就将这两个元素进行交换。这样关键字较小的那个元素就像一个泡泡一样,从最后面冒到最前面来
2、时间复杂度
最好情况下:正序有序,则只需要比较n次。故,为O(n)
最坏情况下: 逆序有序,则需要比较(n-1)+(n-2)+……+1,故,为O(N*N)
3、稳定性
排序过程中只交换相邻两个元素的位置。因此,当两个数相等时,是没必要交换两个数的位置的。所以,它们的相对位置并没有改变,冒泡排序算法是稳定的!
代码
1 void BubbleSort(int a[], int n) 2 { 3 for(int i = 0 ; i < n; i++) 4 { 5 for(int j = n-1; j > i; j--) 6 { 7 if(a[j] < a[j - 1]) 8 { 9 swap(a[j], a[j - 1]); 10 } 11 } 12 } 13 }
二、插入排序
1、思想:如下图所示,每次选择一个元素K插入到之前已排好序的部分A[1…i]中,插入过程中K依次由后向前与A[1…i]中的元素进行比较。若发现发现A[x]>=K,则将K插入到A[x]的后面,插入前需要移动元素。
2、算法时间复杂度。
最好的情况下:正序有序(从小到大),这样只需要比较n次,不需要移动。因此时间复杂度为O(n)
最坏的情况下:逆序有序,这样每一个元素就需要比较n次,共有n个元素,因此实际复杂度为O(n2)
平均情况下:O(n2)
3、稳定性。
理解性记忆比死记硬背要好。因此,我们来分析下。稳定性,就是有两个相同的元素,排序先后的相对位置是否变化,主要用在排序时有多个排序规则的情况下。在插入排序中,K1是已排序部分中的元素,当K2和K1比较时,直接插到K1的后面(没有必要插到K1的前面,这样做还需要移动!!),因此,插入排序是稳定的。
代码
1 void InsertSort(int a[], int n)
2 {
3 int i , j;
4 for(i = 1 ; i < n; i++)
5 {
6 int tmp = a[i];
7 for(j = i - 1; j >= 0; j--)
8 {
9 if(tmp < a[j])
10 { // 向后移动一位,因为a[i]的值赋给了k,所以直接赋值即可
11 a[j+1] = a[j];
12 }
13 else break;
14 }
15 a[j+1] = tmp;
16 }
17 }
三、希尔排序(插入排序)
1、思想:希尔排序也是一种插入排序方法,实际上是一种分组插入方法。先取定一个小于n的整数d1作为第一个增量,把表的全部记录分成d1个组,所有距离为d1的倍数的记录放在同一个组中,在各组内进行直接插入排序;然后,取第二个增量d2(<d1),重复上述的分组和排序,直至所取的增量dt=1(dt<dt-1<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
例如:将 n 个记录分成 d 个子序列:
{ R[0], R[d], R[2d],…, R[kd] }
{ R[1], R[1+d], R[1+2d],…,R[1+kd] }
…
{ R[d-1],R[2d-1],R[3d-1],…,R[(k+1)d-1] }
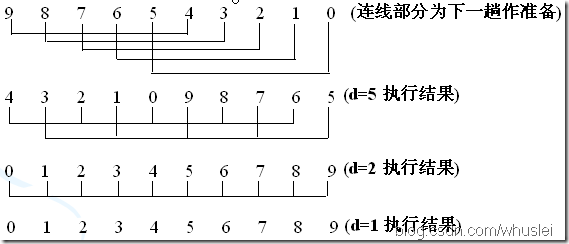
说明:d=5 时,先从A[d]开始向前插入,判断A[d-d],然后A[d+1]与A[(d+1)-d]比较,如此类推,这一回合后将原序列分为d个组。<由后向前>
2、时间复杂度。
最好情况:由于希尔排序的好坏和步长d的选择有很多关系,因此,目前还没有得出最好的步长如何选择(现在有些比较好的选择了,但不确定是否是最好的)。所以,不知道最好的情况下的算法时间复杂度。
最坏情况下:O(N*logN),最坏的情况下和平均情况下差不多。
平均情况下:O(N*logN)
3、稳定性。
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。(有个猜测,方便记忆:一般来说,若存在不相邻元素间交换,则很可能是不稳定的排序。)
代码:
1 void ShellSort(int a[], int n, int d) 2 { 3 int i,j,k,len; 4 for( len = d; len >= 1; len--)// 步长 5 { 6 for( k = 0 ; k < len ; k++)// 分组的起始位置 7 { 8 // 下面就是插入排序 9 for(i = k + len ; i < n; i+=len) 10 { 11 int tmp = a[i]; 12 for(j = i - len; j >= 0; j-=len) 13 { 14 if( tmp < a[j]) 15 a[j+len] = a[j]; 16 else break; 17 } 18 a[j+len] = tmp; 19 } 20 } 21 } 22 }
标签:
原文地址:http://www.cnblogs.com/acSzz/p/5264056.html