标签:
这里我想说明的是
粒子群的收敛里面可能会有的错误
我选用了一个三峰曲面
而粒子群很容易陷入局部最大值
所以得出的值不一定是全局最大值。
哈哈哈,粒子群算法结束了,
接下来我应该是去学BP神经网络。
就是这么任性
main.m
clear all;close all;clc;
x=linspace(-3,3,500);
y=linspace(-3,3,500);
[x,y]=meshgrid(x,y) ;
z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2)
mesh(x,y,z);
hold on;
n=10; %粒子群粒子个数
%初始化粒子群,定义结构体
%结构体中八个元素,分别是粒子坐标,粒子速度,粒子适应度,粒子最佳适应度,粒子最佳坐标
par=struct([]);
for i=1:n
par(i).x=-4+8*rand(); %[-4 4]对x位置随机初始化
par(i).y=-4+8*rand(); %[-4 4]对y位置随机初始化
par(i).vx=-0.1+0.2*rand(); %[-0.1 0.1]对vx速度随机初始化
par(i).vy=-0.1+0.2*rand(); %[-0.1 0.1]对vy速度随机初始化
par(i).fit=0; %粒子适应度为0初始化
par(i).bestfit=0; %粒子最佳适应度为0初始化
par(i).bestx=par(i).x; %粒子x最佳位置初始化
par(i).besty=par(i).y; %粒子y最佳位置初始化
end
par_best=par(1); %初始化粒子群中最佳粒子
for k=1:10
plot3(par_best.x,par_best.y,par_best.fit,‘g*‘); %画出最佳粒子的位置,为相对偏移
for p=1:n
[par(p) par_best]=update_par(par(p),par_best); %更新每个粒子信息
end
end
compute_fit.m
function re=compute_fit(par)
x=par.x;
y=par.y;
sigma=50;
if x<-4 || x>4 || y<-4 || y>4
re=0; %超出范围适应度为0
else %否则适应度按目标函数求解
re= 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2);
end
end
update_par.m
function [par par_best]=update_par(par,par_best)
%Px=Px+Pv*t,这里t=1,Px为当前粒子的位置,Pv为当前粒子的速度
par.x=par.x+par.vx;
par.y=par.x+par.vy;
par.fit=compute_fit(par); %计算当前粒子适应度
%Pv=Pv+(c1*rand*(Gx-Px))+(c2*rand*(PBx-Px))
%这里c1,c2为加速因子
%Gx为具有最佳适应度粒子的位置
%PBx为当前粒子的最佳位置
c1=1;
c2=1;
par.vx=par.vx+c1*rand()*(par_best.x-par.x)+c2*rand()*(par.bestx-par.x);
par.vy=par.vy+c1*rand()*(par_best.y-par.y)+c2*rand()*(par.besty-par.y);
if par.fit>par.bestfit %如果当前粒子适应度要好于当前粒子最佳适应度
par.bestfit=par.fit; %则更新当前粒子最佳适应度
par.bestx=par.x; %更新当前粒子最佳位置
par.besty=par.y;
if par.bestfit>par_best.fit %如果当前粒子最佳适应度好于最佳粒子适应度
par_best.fit=par.bestfit; %则更新最佳粒子适应度
par_best.x=par.x; %更新最佳粒子位置
par_best.y=par.y;
end
end
end
最后是大家最喜欢的图
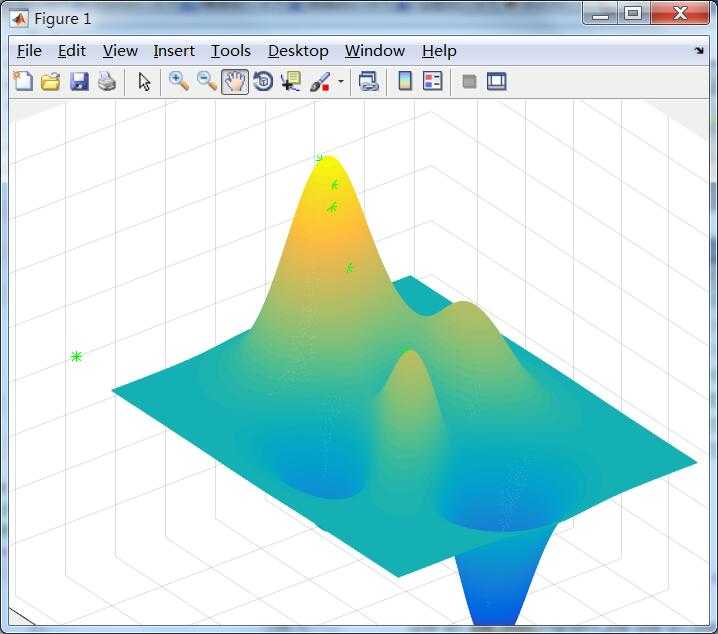
这是正常收敛得到的最大值
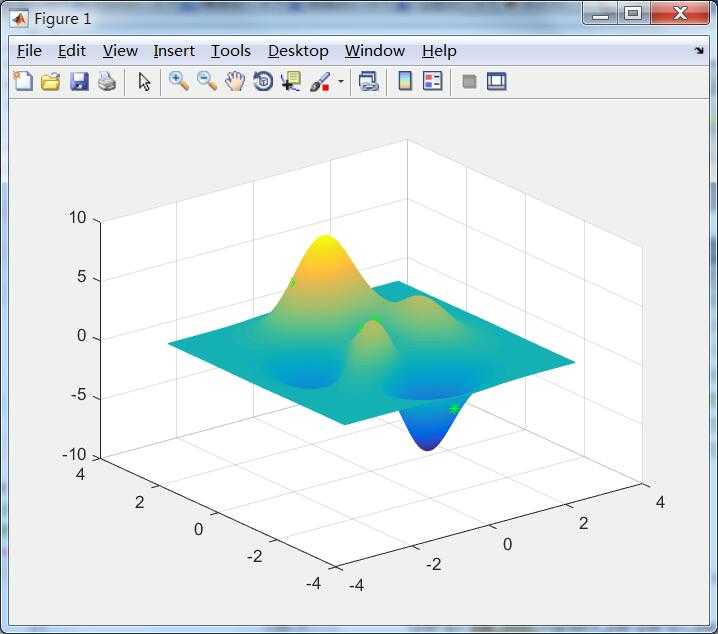
这是错误收敛得到最大值,可见在局部最大值上。
标签:
原文地址:http://www.cnblogs.com/MnsterLu/p/5565599.html