2. Layers used to build ConvNets

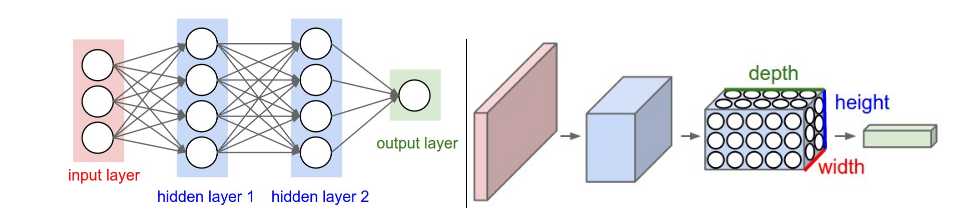
Three main types of layers to build ConvNet architectures: Convolutional Layer, Pooling Layer, and Fully-Connected Layer (exactly as seen in regular Neural Networks).

Example Architecture: a simple ConvNet for CIFAR-10 classification could have the architecture [INPUT - CONV - RELU - POOL - FC]. In more detail:

• INPUT [32x32x3] an image of width 32, height 32, and with three color channels R,G,B.
• CONV layer will compute a dot product between their weights and a small region they are connected to in the input volume. This may result in volume such as [32x32x12] if we decided to use 12 filters.
• RELU layer will apply an elementwise activation function, such as the max(0,x) thresholding at zero. This leaves the size of the volume unchanged ([32x32x12]).
• POOL layer will perform a downsampling operation along the spatial dimensions (width, height), resulting in volume such as [16x16x12].
• FC (i.e. fully-connected) layer will compute the class scores, resulting in volume of size [1x1x10], where each of the 10 numbers correspond to a class score, such as among the 10 categories of CIFAR-10. As with ordinary Neural Networks and as the name implies, each neuron in this layer will be connected to all the numbers in the previous volume.

The CONV/FC layers perform transformations that are a function of the activations in the input volume and the parameters (the weights and biases of the neurons). 

The parameters in the CONV/FC layers will be trained with gradient descent

The RELU/POOL layers will implement a fixed function

2.1 Convolutional Layer

Neuron size

The connections are local in space (along width and height), but always full along the entire depth of the input volume.

Example 1. For example, input volume has size [32x32x3], If the receptive field (or the filter size) is 5x5, then each neuron in the Conv Layer will have weights to a [5x5x3] region in the input volume, for a total of 5*5*3 = 75 weights (and +1 bias parameter). Notice that the extent of the connectivity along the depth axis must be 3, since this is the depth of the input volume.

Example 2. Suppose an input volume had size [16x16x20]. Then using an example receptive field size of 3x3, every neuron in the Conv Layer would now have a total of 3*3*20 = 180 connections to the input volume. Notice that, again, the connectivity is local in space (e.g. 3x3), but full along the input depth (20).

Spatial arrangement

Three hyperparameters：depth, stride and zero-padding.

depth：number of filters we would like to use

input volume size in one dimension (W), the receptive field size of the Conv Layer neurons (F), the stride size (S), and the amount of zero padding used (P)

output size: (W?F+2P)/S+1

Summary

• Accepts a volume of size W1×H1×D1W1×H1×D1
• Requires four hyperparameters:
  • Number of filters KK,
  • their spatial extent FF,
  • the stride SS,
  • the amount of zero padding PP.
• Produces a volume of size W2×H2×D2W2×H2×D2 where:With parameter sharing, it introduces F?F?D1F?F?D1 weights per filter, for a total of (F?F?D1)?K(F?F?D1)?K weights and KK biases.
  • W2=(W1?F+2P)/S+1W2=(W1?F+2P)/S+1
  • H2=(H1?F+2P)/S+1H2=(H1?F+2P)/S+1 (i.e. width and height are computed equally by symmetry)
  • D2=KD2=K
• In the output volume, the dd-th depth slice (of size W2×H2W2×H2) is the result of performing a valid convolution of the dd-th filter over the input volume with a stride of SS, and then offset by dd-th bias.

A common setting of the hyperparameters is F=3,S=1,P=1F=3,S=1,P=1.

2.2 Pooling Layer

Its function is to progressively reduce the spatial size of the representation to reduce the amount of parameters and computation in the network, and hence to also control overfitting. 

The Pooling Layer operates independently on every depth slice of the input and resizes it spatially, using the MAX operation.

The most common form is a pooling layer with filters of size 2x2 applied with a stride of 2 downsamples every depth slice in the input by 2 along both width and height, discarding 75% of the activations.

• Accepts a volume of size W1×H1×D1W1×H1×D1
• Requires two hyperparameters:
  • their spatial extent FF,
  • the stride SS,
• Produces a volume of size W2×H2×D2W2×H2×D2 where:Introduces zero parameters since it computes a fixed function of the input
  • W2=(W1?F)/S+1W2=(W1?F)/S+1
  • H2=(H1?F)/S+1H2=(H1?F)/S+1
  • D2=D1D2=D1
• Note that it is not common to use zero-padding for Pooling layers

2.3 Fully-connected layer

Neurons in a fully connected layer have full connections to all activations in the previous layer, as seen in regular Neural Networks. Their activations can hence be computed with a matrix multiplication followed by a bias offset. 

3. ConvNet Architectures

3.1 Layer Patterns

the most common ConvNet architecture follows the pattern:

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

for example

• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC Here we see two CONV layers stacked before every POOL layer. This is generally a good idea for larger and deeper networks, because multiple stacked CONV layers can develop more complex features of the input volume before the destructive pooling operation.

Prefer a stack of small filter CONV to one large receptive field CONV layer.

Suppose that you stack three 3x3 CONV layers on top of each other (with non-linearities in between, of course). In this arrangement, each neuron on the first CONV layer has a 3x3 view of the input volume. A neuron on the second CONV layer has a 3x3 view of the first CONV layer, and hence by extension a 5x5 view of the input volume. Similarly, a neuron on the third CONV layer has a 3x3 view of the 2nd CONV layer, and hence a 7x7 view of the input volume. Suppose that instead of these three layers of 3x3 CONV, we only wanted to use a single CONV layer with 7x7 receptive fields. These neurons would have a receptive field size of the input volume that is identical in spatial extent (7x7), but with several disadvantages. First, the neurons would be computing a linear function over the input, while the three stacks of CONV layers contain non-linearities that make their features more expressive. Second, if we suppose that all the volumes have CC channels, then it can be seen that the single 7x7 CONV layer would contain C×(7×7×C)=49C^2 parameters, while the three 3x3 CONV layers would only contain 3×(C×(3×3×C))=27C^2 parameters. Intuitively, stacking CONV layers with tiny filters as opposed to having one CONV layer with big filters allows us to express more powerful features of the input, and with fewer parameters. As a practical disadvantage, we might need more memory to hold all the intermediate CONV layer results if we plan to do backpropagation.

3.2 Layer Sizing Patterns

The input layer (that contains the image) should be divisible by 2 many times. Common numbers include 32 (e.g. CIFAR-10), 64, 96 (e.g. STL-10), or 224 (e.g. common ImageNet ConvNets), 384, and 512.

The conv layers should be using small filters (e.g. 3x3 or at most 5x5), using a stride of S=1S=1, and crucially, padding the input volume with zeros in such way that the conv layer does not alter the spatial dimensions of the input.

For a general F, it can be seen that P=(F?1)/2 preserves the input size. If you must use bigger filter sizes (such as 7x7 or so), it is only common to see this on the very first conv layer that is looking at the input image.

The pool layers are in charge of downsampling the spatial dimensions of the input. The most common setting is to use max-pooling with 2x2 receptive fields (i.e. F=2F=2), and with a stride of 2 (i.e. S=2S=2)

Why use stride of 1 in CONV? 

Smaller strides work better in practice. Additionally, as already mentioned stride 1 allows us to leave all spatial down-sampling to the POOL layers, with the CONV layers only transforming the input volume depth-wise.

Why use padding? 

In addition to the aforementioned benefit of keeping the spatial sizes constant after CONV, doing this actually improves performance. If the CONV layers were to not zero-pad the inputs and only perform valid convolutions, then the size of the volumes would reduce by a small amount after each CONV, and the information at the borders would be “washed away” too quickly.

Transfer Learning

In practice, very few people train an entire Convolutional Network from scratch (with random initialization), because it is relatively rare to have a dataset of sufficient size. Instead, it is common to pretrain a ConvNet on a very large dataset (e.g. ImageNet, which contains 1.2 million images with 1000 categories), and then use the ConvNet either as an initialization or a fixed feature extractor for the task of interest. The three major Transfer Learning scenarios look as follows:

• ConvNet as fixed feature extractor.　　Take a ConvNet pretrained on ImageNet, remove the last fully-connected layer (this layer’s outputs are the 1000 class scores for a different task like ImageNet), then treat the rest of the ConvNet as a fixed feature extractor for the new dataset. In an AlexNet, this would compute a 4096-D vector for every image that contains the activations of the hidden layer immediately before the classifier. We call these features CNN codes. It is important for performance that these codes are ReLUd (i.e. thresholded at zero) if they were also thresholded during the training of the ConvNet on ImageNet (as is usually the case). Once you extract the 4096-D codes for all images, train a linear classifier (e.g. Linear SVM or Softmax classifier) for the new dataset.

• Fine-tuning the ConvNet.　　 The second strategy is to not only replace and retrain the classifier on top of the ConvNet on the new dataset, but to also fine-tune the weights of the pretrained network by continuing the backpropagation. It is possible to fine-tune all the layers of the ConvNet, or it’s possible to keep some of the earlier layers fixed (due to overfitting concerns) and only fine-tune some higher-level portion of the network. This is motivated by the observation that the earlier features of a ConvNet contain more generic features (e.g. edge detectors or color blob detectors) that should be useful to many tasks, but later layers of the ConvNet becomes progressively more specific to the details of the classes contained in the original dataset. In case of ImageNet for example, which contains many dog breeds, a significant portion of the representational power of the ConvNet may be devoted to features that are specific to differentiating between dog breeds.

When and how to fine-tune? How do you decide what type of transfer learning you should perform on a new dataset? This is a function of several factors, but the two most important ones are the size of the new dataset (small or big), and its similarity to the original dataset (e.g. ImageNet-like in terms of the content of images and the classes, or very different, such as microscope images). Keeping in mind that ConvNet features are more generic in early layers and more original-dataset-specific in later layers, here are some common rules of thumb for navigating the 4 major scenarios:

1. New dataset is small and similar to original dataset. Since the data is small, it is not a good idea to fine-tune the ConvNet due to overfitting concerns. Since the data is similar to the original data, we expect higher-level features in the ConvNet to be relevant to this dataset as well. Hence, the best idea might be to train a linear classifier on the CNN codes.
2. New dataset is large and similar to the original dataset. Since we have more data, we can have more confidence that we won’t overfit if we were to try to fine-tune through the full network.
3. New dataset is small but very different from the original dataset. Since the data is small, it is likely best to only train a linear classifier. Since the dataset is very different, it might not be best to train the classifier form the top of the network, which contains more dataset-specific features. Instead, it might work better to train the SVM classifier from activations somewhere earlier in the network.
4. New dataset is large and very different from the original dataset. Since the dataset is very large, we may expect that we can afford to train a ConvNet from scratch. However, in practice it is very often still beneficial to initialize with weights from a pretrained model. In this case, we would have enough data and confidence to fine-tune through the entire network.

Practical advice. There are a few additional things to keep in mind when performing Transfer Learning:

• Constraints from pretrained models. Note that if you wish to use a pretrained network, you may be slightly constrained in terms of the architecture you can use for your new dataset. For example, you can’t arbitrarily take out Conv layers from the pretrained network. However, some changes are straight-forward: Due to parameter sharing, you can easily run a pretrained network on images of different spatial size. This is clearly evident in the case of Conv/Pool layers because their forward function is independent of the input volume spatial size (as long as the strides “fit”). In case of FC layers, this still holds true because FC layers can be converted to a Convolutional Layer: For example, in an AlexNet, the final pooling volume before the first FC layer is of size [6x6x512]. Therefore, the FC layer looking at this volume is equivalent to having a Convolutional Layer that has receptive field size 6x6, and is applied with padding of 0.
• Learning rates. It’s common to use a smaller learning rate for ConvNet weights that are being fine-tuned, in comparison to the (randomly-initialized) weights for the new linear classifier that computes the class scores of your new dataset. This is because we expect that the ConvNet weights are relatively good, so we don’t wish to distort them too quickly and too much (especially while the new Linear Classifier above them is being trained from random initialization).