标签:二叉树 == 非递归 svi create util null 遍历 size
二叉树(BinaryTree)是n(n≥0)个结点的有限集,它或者是空集(n=0),或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。
这个定义是递归的。由于左、右子树也是二叉树, 因此子树也可为空树。
五种不同基本形态的二叉树:
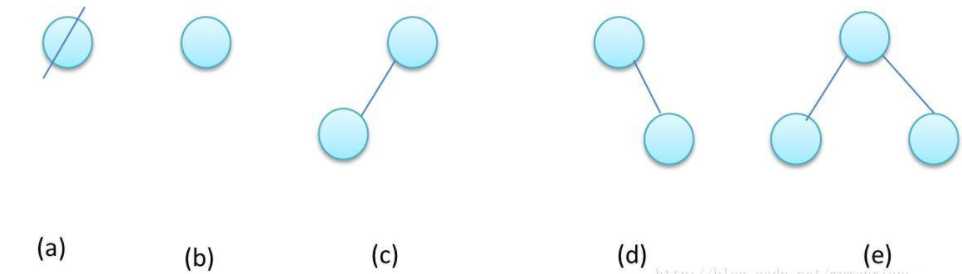
对于二叉树来讲最主要、最基本的运算是遍历。
遍历二叉树 是指以一定的次序访问二叉树中的每个结点。所谓 访问结点 是指对结点进行各种操作的简称。例如,查询结点数据域的内容,或输出它的值,或找出结点位置,或是执行对结点的其他操作。遍历二叉树的过程实质是把二叉树的结点进行线性排列的过程。假设遍历二叉树时访问结点的操作就是输出结点数据域的值,那么遍历的结果得到一个线性序列。
从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)访问结点本身(N),
(2)遍历该结点的左子树(L),
(3)遍历该结点的右子树(R)。
以上三种操作有六种执行次序:
NLR、LNR、LRN、NRL、RNL、RLN。
注意:
前三种次序与后三种次序对称,故只讨论先左后右的前三种次序。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtlee)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
import java.util.Stack;
/**
*
* @ClassName: BinaryTree
* @Description: 二叉树的链式存储
* @author:
* @date:
*/
public class BinaryTree {
private TreeNode root=null;
public BinaryTree() {
root=new TreeNode(1,"rootNode(A)");
}
/**
*
* @ClassName: TreeNode
* @Description: 二叉树的节点数据结构
* @author:
* @date:
*/
public class TreeNode {
private int key=0;
private String data=null;
private boolean isVisted=false;
private TreeNode leftChild=null;
private TreeNode rightChild=null;
public TreeNode() {
}
/**
* @param key 层序编码
* @param data 数据域
*/
private TreeNode(int key, String data) {
this.key = key;
this.data = data;
this.leftChild=null;
this.rightChild=null;
}
}
/**
* 创建一棵二叉树
* <pre>
* A
* B C
* D E F
* </pre>
* @param root
*/
public void createBinTree(TreeNode root){
TreeNode newNodeB=new TreeNode(2, "B");
TreeNode newNodeC=new TreeNode(2, "C");
TreeNode newNodeD=new TreeNode(2, "D");
TreeNode newNodeE=new TreeNode(2, "E");
TreeNode newNodeF=new TreeNode(2, "F");
root.leftChild=newNodeB;
root.rightChild=newNodeC;
root.leftChild.leftChild=newNodeD;
root.leftChild.rightChild=newNodeE;
root.rightChild.rightChild=newNodeF;
}
public boolean isEmpty(){
return root==null;
}
//树的高度
public int height(){
return height(root);
}
//节点个数
public int size(){
return size(root);
}
private int height(TreeNode subTree){
if(subTree==null)
return 0;//递归结束:空树高度为0
else {
int i=height(subTree.leftChild);
int j=height(subTree.rightChild);
return (i<j)?(j+1):(i+1);
}
}
private int size(TreeNode subTree){
if(subTree==null)
return 0;
else {
return 1+size(subTree.leftChild)+size(subTree.rightChild);
}
}
//返回双亲结点
public TreeNode parent(TreeNode element){
return (root==null || root==element)? null:parent(root,element);
}
public TreeNode parent(TreeNode subTree,TreeNode element){
if(subTree==null)
return null;
if(subTree.leftChild==element||subTree.rightChild==element)
return subTree;//返回父结点地址
TreeNode p;
//先在左子树中找,如果左子树中没有找到,才到右子树去找
if((p=parent(subTree.leftChild,element))!=null)
//递归在左子树中搜索
return p;
else
//递归在右子树中搜索
return parent(subTree.rightChild, element);
}
public TreeNode getLeftChildNode(TreeNode element){
return (element!=null)? element.leftChild:null;
}
public TreeNode getRightChildNode(TreeNode element){
return (element!=null)? element.rightChild:null;
}
public TreeNode getRoot(){
return root;
}
//在释放某个结点时,该结点的左右子树都已经释放,
//所以应该采用后续遍历,当访问某个结点时将该结点的存储空间释放
public void destroy(TreeNode subTree){
if(subTree!=null)
destroy(subTree.leftChild); //删除左子树
destroy(subTree.rightChild);//删除右子树
subTree=null;//删除根结点
}
public void traverse(TreeNode subTree){
System.out.println("key:"+subTree.key+";name:"+subTree.data);
traverse(subTree.leftChild);
traverse(subTree.rightChild);
}
public void visted(TreeNode subTree){
subTree.isVisted=true;
System.out.println("key:"+subTree.key+";name:"+subTree.data);
}
//前序遍历
public void preOrder(TreeNode subTree){
if(subTree!=null){
visted(subTree);
preOrder(subTree.leftChild);
preOrder(subTree.rightChild);
}
}
//中序遍历
public void inOrder(TreeNode subTree){
if(subTree!=null){
inOrder(subTree.leftChild);
visted(subTree);
inOrder(subTree.rightChild);
}
}
//后续遍历
public void postOrder(TreeNode subTree){
if(subTree!=null){
postOrder(subTree.leftChild);
postOrder(subTree.rightChild);
visted(subTree);
}
}
//前序遍历的非递归实现
public void nonRecPreOder(TreeNode p){
Stack<TreeNode> stack=new Stack<TreeNode>();
TreeNode node=p;
while(node!=null||stack.size()>0){
while(node!=null){
visted(node);
stack.push(node);
node=node.leftChild;
}
while(stack.size()>0){
node=stack.pop();
node=node.rightChild;
}
}
}
//中序遍历的非递归实现
public void nonRecInOrder(TreeNode p){
Stack<TreeNode> stack =new Stack<BinaryTree.TreeNode>();
TreeNode node =p;
while(node!=null||stack.size()>0){
//存在左子树
while(node!=null){
stack.push(node);
node=node.leftChild;
}
//栈非空
if(stack.size()>0){
node=stack.pop();
visted(node);
node=node.rightChild;
}
}
}
//后序遍历的非递归实现
public void noRecPostOrder(TreeNode p){
Stack<TreeNode> stack=new Stack<BinaryTree.TreeNode>();
TreeNode node =p;
while(p!=null){
//左子树入栈
for(;p.leftChild!=null;p=p.leftChild){
stack.push(p);
}
//当前结点无右子树或右子树已经输出
while(p!=null&&(p.rightChild==null||p.rightChild==node))
{
visted(p);
//纪录上一个已输出结点
node =p;
if(stack.empty())
return;
p=stack.pop();
}
//处理右子树
stack.push(p);
p=p.rightChild;
}
}
public static void main(String[] args) {
BinaryTree bt=new BinaryTree();
bt.createBinTree(bt.root);
System.out.println("the size of the tree is :" + bt.size());
System.out.println("the height of the tree is :" + bt.height());
System.out.println("*******(前序遍历)[ABDECF]遍历*****************");
bt.preOrder(bt.root);
System.out.println("*******(中序遍历)[DBEACF]遍历*****************");
bt.inOrder(bt.root);
System.out.println("*******(后序遍历)[DEBFCA]遍历*****************");
bt.postOrder(bt.root);
System.out.println("***非递归实现****(前序遍历)[ABDECF]遍历*****************");
bt.nonRecPreOder(bt.root);
System.out.println("***非递归实现****(中序遍历)[DBEACF]遍历*****************");
bt.nonRecInOrder(bt.root);
System.out.println("***非递归实现****(后序遍历)[DEBFCA]遍历*****************");
bt.noRecPostOrder(bt.root);
}
}
标签:二叉树 == 非递归 svi create util null 遍历 size
原文地址:http://www.cnblogs.com/ipetergo/p/6862111.html