标签:最大 logs 通用 called pre print lowbit 区间 16px
问题描述:给定一序列,求任意区间(i, j)的元素和;修改任意一元素,实现快速更新
树状数组
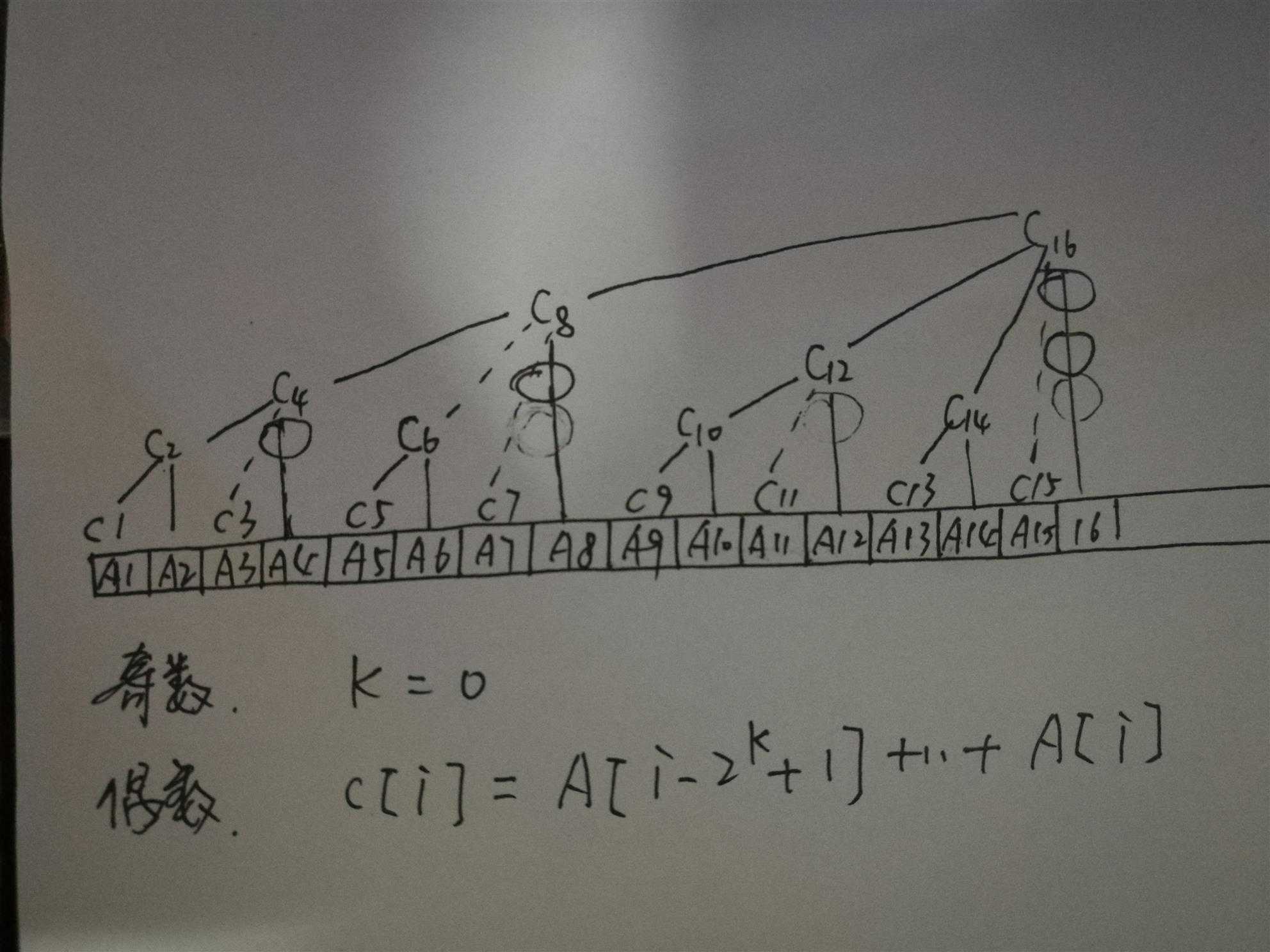
树状数组的主要特点是生成一棵树,树的高度为logN。每一层的高度为k,分布在这一层的序列元素索引的二进制表达有个共同的特点,就是最低二次幂为k。
子树间有很强的联系,即,给定一序列元素索引i,可以推知该元素所在节点C[i]的父节点C[p],p=i+2^k,其中k=i & (i ^ (i-1)),以及该元素所在子树的前一子树的根节点p=i-2^k。
子树间的联系可以很方便地用于求前n个元素的和,即找到所有子树即可;为实现更新,也只需要logN步操作,实现C[i]值的更新和序列元素的更新。
# leetcode 307
# 树状数组
# 树状数组的本质还是二分树,从而达到O(logN)的算法复杂度
# 树状数组最有趣的地方在于最底层高度为0,序列的第i项的高度为k,k代表i的二进制中从右数0的位数,即2次幂的最低次
# 从二进制的角度来看,很快可以得出结论 2^k = i & (i ^ (i - 1))
# 给出一节点i,可以快速找到它的父节点(i + 2^k)和该节点前的最近一棵子树的根结点(i - 2^k)
# 问题形式:
# 1. 给定一固定序列,求索引n前所有项和:相当于求所有子树的根节点值之和
# 2. 对固定序列任意修改一元素,实现快速更新:相当于更新包含该结点的所有子树的根节点的值
# 最纠结的地方还是求根节点数组C,没想到是通过update求。
class NumArray(object):
def __init__(self, nums):
"""
:type nums: List[int]
"""
self.nums = [0 for _ in nums]
self.n = len(nums)
self.c = [0 for _ in nums]
for i, num in enumerate(nums):
self.update(i, num)
def lowBit(self, x):
## return x & (-x)
return x & (x ^ (x - 1))
def update(self, i, val):
"""
:type i: int
:type val: int
:rtype: void
"""
difference = val - self.nums[i]
self.nums[i] = val
while i < self.n:
self.c[i] += difference
i += self.lowBit(i + 1)
def getSum(self, n):
sum = 0
while n >= 0:
sum += self.c[n]
n -= self.lowBit(n + 1)
return sum
def sumRange(self, i, j):
"""
:type i: int
:type j: int
:rtype: int
"""
return self.getSum(j) - self.getSum(i) + self.nums[i]
# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(i,val)
# param_2 = obj.sumRange(i,j)
nums = [1, 3, 5]
X = NumArray(nums)
# X.update(0, 1)
print(X.sumRange(0, 2))
# print(X.getSum(0))
线段树
线段树是一种满二分树,即每个节点的度为0或2.
线段树的主要特点是不断平分区间[s, e]为[s, mid]和[mid + 1, e],其中mid = s + int((e - s) / 2)。称度为0的结点为叶节点,即只包含一个数,不再平分。
线段树的构造是通过构造结点,由其平分性质可知,若给定序列长度为N,则叶节点数目为N,非叶节点为N - 1,即一共2N - 1个结点。定义根节点的索引为0,其左子树的结点为1, 右子树的结点为2。通用地说,若当前结点为i,则其左结点为(2 * i + 1),右结点为(2 * i + 2),因此,构造结点数目时,索引长度不是N-1。(具体为多少我也还不知道,有博文说是2 * 2 ^(ceil(logN))) - 1,但数据量一大leetcode上就死活通不过)同样地,线段树可以用于求和和更新。非常巧妙!线段树的操作基本都是基于递归函数,先给一个总区间(也就是根节点对应的区间),然后不断平分,求 getSbSumUntil(ss, mid, qs, qe, (2 * si) + 1) +
getSbSumUntil(mid + 1, se, qs, qe, (2 * si) + 2)
此外,线段树还可以用于求区间和最大和区间替换,下次说。
# leetcode 307
# 线段树
import math
class NumArray(object):
def __init__(self, nums):
"""
:type nums: List[int]
"""
self.nums = nums
self.n = len(nums)
self.st = [0 for _ in range(2 * 2 ^ int(math.log2(self.n)))]
self.constructSTUntil(0, self.n - 1, 0)
def getMid(self, s, e):
return int(s + (e - s) / 2)
def constructSTUntil(self, ss, se, si):
if ss == se:
self.st[si] = self.nums[ss]
return self.st[si]
mid = self.getMid(ss, se)
self.st[si] = self.constructSTUntil(ss, mid, (2 * si) + 1) + self.constructSTUntil(mid + 1, se, (2 * si) + 2)
return self.st[si]
def updataUntil(self, ss, se, i, si, difference):
if i < ss or i > se:
return
self.st[si] += difference
if ss != se:
mid = self.getMid(ss, se)
self.updataUntil(ss, mid, i, (2 * si + 1), difference)
self.updataUntil(mid + 1, se, i, (2 * si + 2), difference)
def update(self, i, val):
"""
:type i: int
:type val: int
:rtype: void
"""
difference = val - self.nums[i]
self.nums[i] = val
self.updataUntil(0, self.n - 1, i, 0, difference)
def getSbSumUntil(self, ss, se, qs, qe, si):
if qs == qe:
return self.nums[qs]
if (qs <= ss) and (qe >= se):
return self.st[si]
if (qs > se) or (qe < ss):
return 0
mid = self.getMid(ss, se)
return self.getSbSumUntil(ss, mid, qs, qe, (2 * si) + 1) + self.getSbSumUntil(mid + 1, se, qs, qe, (2 * si) + 2)
def sumRange(self, i, j):
"""
:type i: int
:type j: int
:rtype: int
"""
return self.getSbSumUntil(0, self.n - 1, i, j, 0)
# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(i,val)
# param_2 = obj.sumRange(i,j)
nums = [-1]
X = NumArray(nums)
X.update(0, 1)
print(X.sumRange(0, 0))
标签:最大 logs 通用 called pre print lowbit 区间 16px
原文地址:http://www.cnblogs.com/fanmu/p/7623031.html