标签:不可 img 带人 标点符号 关心 映射 范围 跳转指令 过程
那要函数干嘛。不都是代码吗?只不过函数是通过一个名字被封装起来的一段代码。有名字就就了不起啊!!!
对啊,有名字就是了不起啊,函数可以通过函数名来调用被其封装起来的代码。
可以理解为是一个变量(函数名)指向的一段代码。这个变量(函数名)只是一段没有执行的代码,变量()(函数名())是表示执行这段代码。
1.代码重用
例如:一段用来求两数之和的代码通过一个函数名封装成一个函数,每当需要求和功能时就不用在把这段代码敲出来了,直接用函数名来调用这段代码
这样这一段求被封装成函数的求和代码就被重复的使用了很多次。(还省了你敲代码的时间)
2.保持一致性
每一个调用的函数都是同一个,代码都都是一样的。
3.易扩展性
因为函数保持一致性,所有修改函数,为函数添加新功能时,只要修改一次,所有调用的该函数都会跟着变。
def 函数名(参数列表):
函数主体(被封装起来的一段代码)
def have_name():
print(‘有名字就是了不起!‘)
have_name() # 用函数名调用函数 have_name函数名是指被封装的代码,have_name()代表是执行这段代码。
想要写出高质量的代码,规范的命名是必不可少的。期待吧,少年,我会开单章随笔来,叨叨这个命名的。
形参:形式上的参数,是应函数的需求虚拟出变量。当调用这个函数时,就会传一个参数(实参)给形参,这样虚拟的变量就变真实了(实参个数,类型应与实参一一对应);
实参:实际参数,调用函数时传给函数的参数,可以是常量,变量,表达式,函数,传给形参 ;
打个比喻来形象的说明形参和实参的关系,在数学的函数 F(X)=X+1 中,X就是形参(这个时候X不代表任何具体的值),而当把X=1带人这个F(X)函数时,1就是实参。
区别:形参是虚拟的,不占用内存空间,形参变量只有在被调用时才分配内存单元,实参是一个变量,占用内存空间。
def tow_sum(a,b): #这个里的a和b是没有分配内存空间的 c=a+b #这里的a和b是分配了内存空间的 print(c) tow_sum(1,2) # 1和2 是实参为其分配了内存空间
函数的形参可以是各种数据(数字,字符串,元组,列表,字典等),函数名等……
def gu(a,b): if a==1: print(‘钟鼓馔玉不足贵,但愿长醉不复醒。‘) if b==2: print(‘古来圣贤皆寂寞,惟有饮者留其名。‘) # 标准调用 gu(1,1) #钟鼓馔玉不足贵,但愿长醉不复醒。 # 关键字调用(可以不按顺序) gu(b=2,a=1) # 钟鼓馔玉不足贵,但愿长醉不复醒。 # 古来圣贤皆寂寞,惟有饮者留其名。
def gu(a=1,b=0): if a==1: print(‘钟鼓馔玉不足贵,但愿长醉不复醒。‘) if b==2: print(‘古来圣贤皆寂寞,惟有饮者留其名。‘) gu() #钟鼓馔玉不足贵,但愿长醉不复醒。 gu(2,2) #古来圣贤皆寂寞,惟有饮者留其名。 gu(b=2,a=0) #古来圣贤皆寂寞,惟有饮者留其名。
非关键字可变长参数(元组):“非关键字”“可变长”顾名思义是允许在调用时传入多个“非关键字”参数,python会将这些多出来的参数放入一个元组中。
def gu(*s): print(type(s)) print(s) gu(1,‘钟鼓馔玉不足贵,但愿长醉不复醒。‘,2,‘古来圣贤皆寂寞,惟有饮者留其名。‘) #可变长,爱有几个参数就调几个参数 # <class ‘tuple‘> 元组 # (1, ‘钟鼓馔玉不足贵,但愿长醉不复醒。‘, 2, ‘古来圣贤皆寂寞,惟有饮者留其名。‘)
关键字可变长参数(字典):“关键字”“可变长”顾名思义是允许在调用时传入多个“关键字”参数,python会将这些多出来的<参数名, 参数值>放入一个字典中。
def gu(**s): print(type(s)) print(s) print(s[‘a‘]) print(s[‘b‘]) gu(a= "钟鼓馔玉不足贵,但愿长醉不复醒。", b= ‘古来圣贤皆寂寞,惟有饮者留其名。‘) #可变长,爱有几个参数就调几个参数 # <class ‘dict‘> 字典 # {‘a‘: ‘钟鼓馔玉不足贵,但愿长醉不复醒。‘, ‘b‘: ‘古来圣贤皆寂寞,惟有饮者留其名。‘} # 钟鼓馔玉不足贵,但愿长醉不复醒。 # 古来圣贤皆寂寞,惟有饮者留其名。
需要注意的是当它们混用时,关键字变量参数应该为函数定义的最后一个参数,带**。调用函数时参数的输入也有不同的方式。
def gu(a,b,*c,**d): print(a) print(b) print(c) print(d) gu(1,2,3,f=7,g=8) # 1 # 2 # (3,) # {‘f‘: 7, ‘g‘: 8} def gu(a,b,*c,**d): print(a) print(b) print(c) print(d) gu(1,2,*(‘钟鼓馔玉不足贵,但愿长醉不复醒‘,),**{‘t‘: ‘钟鼓馔玉不足贵,但愿长醉不复醒。‘, ‘f‘: ‘古来圣贤皆寂寞,惟有饮者留其名。‘}) # 1 # 2 # (‘钟鼓馔玉不足贵,但愿长醉不复醒‘,) # {‘t‘: ‘钟鼓馔玉不足贵,但愿长醉不复醒。‘, ‘f‘: ‘古来圣贤皆寂寞,惟有饮者留其名。‘}
要想获取函数的执行结果,就可以用return语句把结果返回
return返回值可以是各种数据(数字,字符串,元组,列表,字典等),函数名等……
注意:
def gu(a): return a b = gu(‘古来圣贤皆寂寞,惟有饮者留其名。‘) print(b)
高阶函数是至少满足下列一个条件的函数:
递归函数,修饰器也都是高阶函数的运用
作用域研究的是数据的适用范围。
就像地球的重力加速度g在火星上就不适用。
def globe(): g = 9.8 def mars(): g = 3.71
上述代码中两个g是毫无关系的,因为它们的作用域不同一个函数就是一个作用域。在globe()中的g的只在globe函数中适用,另一个g也是是如此。
这只是作用域的小小体现,作用域不只在函数中有,在类,包中都有体现 。还有如何去调用,修改不同作用域里的数据。
这些都会开单章来唠叨一下。
定义:一个函数在内部调用自身本身,这个函数就是递归函数。
说白了就是自己和自己玩(单身人士都懂的)
注意:
1. 必须有一个明确的结束条件 (不可自娱自乐太久要有个度)
2. 每次进入更深一层递归时,问题规模相比上次递归都应有所减少 (每自娱自乐一次总得缓解一下单身狗的苦)
3. 递归效率不高,递归层次过多会导致栈溢出。(自娱自乐多了伤身)
注释:(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数执行结束,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出。)
阶乘的计算
# **********循环********* def factorial(n): result = n for i in range(1, n): result *= i return result print(factorial(3)) # **********递归********* def factorial_new(n): if n == 1: # 递归结束条件 return 1 result=factorial_new(n - 1) result = n * result return result a = factorial_new(3) print(a)
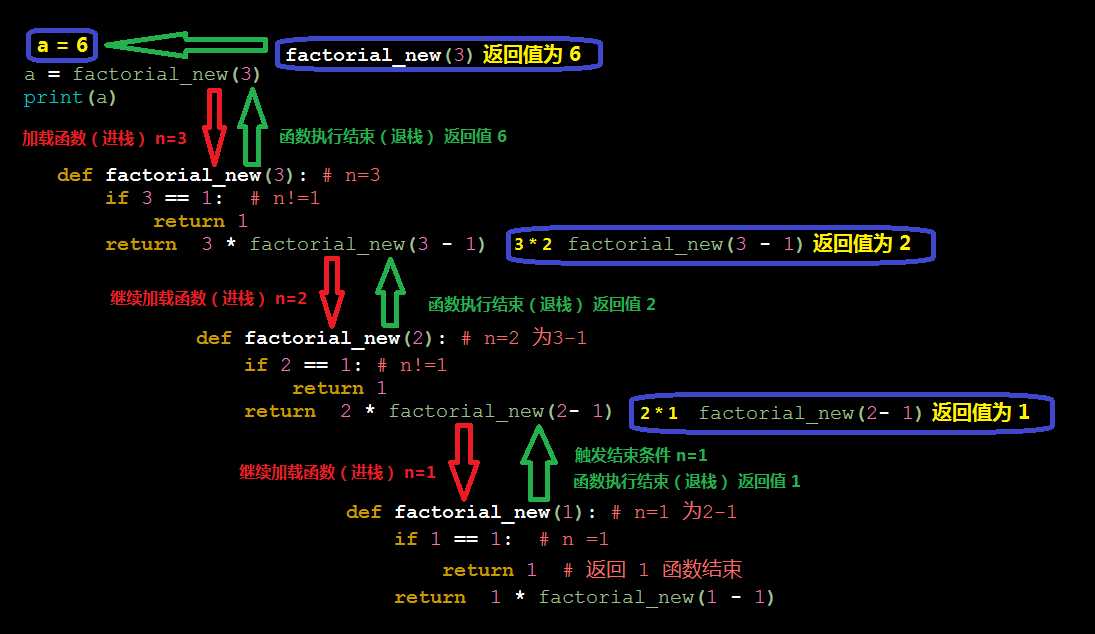
递归函数是定义简单,逻辑清晰。理论上,所有的递归函数都可以写成循环的方式,但循环的逻辑不如递归清晰。
内置函数就是Python提供的,可以直接使用的函数,所以内置函数一般都是使用频繁的函数。
以后会仔细说一下有哪些内置函数
常见的编程范式有命令式编程,函数式编程。
命令式编程:是面向计算机硬件的抽象,有变量(对应着存储单元),赋值语句(获取,存储指令),表达式(内存引用和算术运算)和控制语句(跳转指令),命令式程序就是一个冯诺依曼机的按照打孔纸带执行指令。
函数式编程:是面向数学的抽象,他将计算机运算看做是数学中函数的计算,并且避免了状态以及变量的概念,一句话,函数式程序就是一个表达式。
面向过程编程,面向对象编程都是命令式编程
#计算列表中数的平均值 #***********命令式编程*************** number = [0,1, 2, 3, 4, 5, 6, 7, 8, 9] count = 0 add = 0 for i in range(len(number)): count += 1 # 第一步 计数 add+= number[i] # 第二步 求和 if count > 0: average = add/ count # 第三步 计算平均数 print(average) #***********函数式编程*************** number = [0,1, 2, 3, 4, 5, 6, 7, 8, 9] average = sum(number) / len(number) print(average)
欢迎评论,番茄,鸡蛋都砸过来吧!!!
标签:不可 img 带人 标点符号 关心 映射 范围 跳转指令 过程
原文地址:https://www.cnblogs.com/barkingpig/p/9104056.html