0.数据结构(python语言) 基本概念 算法的代价及度量！！！

标签：一对多   数据结构   image   nlogn   输入参数   ima   3.1   存储管理   内存   

先看思维导图：

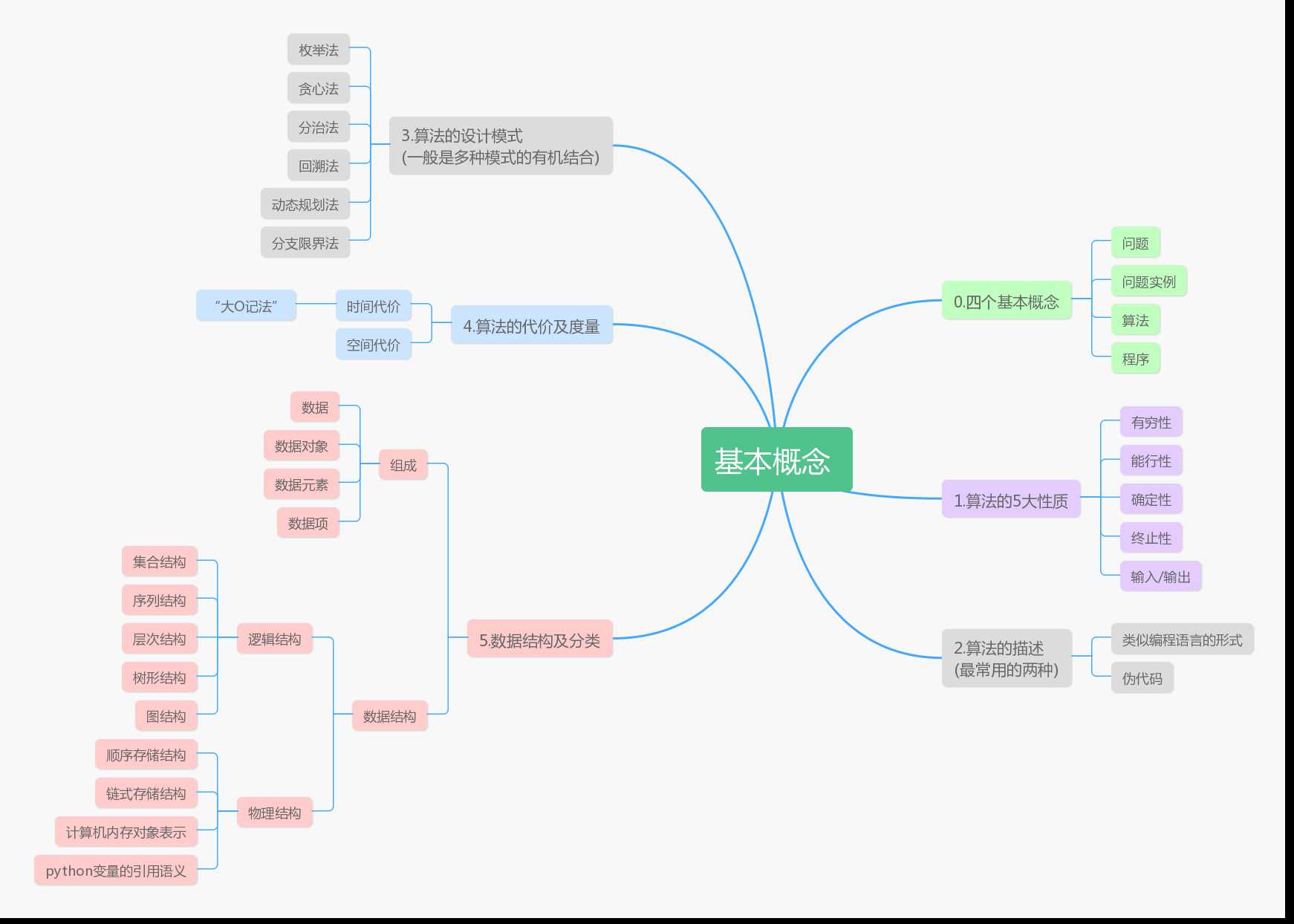
*思维导图有点简陋，本着循循渐进的思想，这小节的知识大多只做了解即可。

*重点在于算法的代价及度量！！！查找资料务必弄清楚.

零.四个基本概念

• 问题：一个具体的需求
• 问题实例：针对问题(需求)的具体的例子
• 算法：解决问题的过程，是对一个计算过程的严格描述
• 程序：程序可以看作是采用计算装置能够处理的语言描述的算法

一.算法的5大性质

• 有穷性（算法描述的又穷性）：算法必须用有限长的描述说清楚
• 能行性：算法的每一步都是可行的，也就是说，每一步都能通过执行有限次数完成
• 确定性：别人看了过后，很清楚的明白，不会有歧义
• 终止性（行为的有穷性）：指算法在执行有限的步骤后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成
• 输入/输出：算法具有零个(print("Hello World"))或多个输入(输入参数)；算法至少有一个或多个输出

二.算法的描述(最常用的两种)

• 类似编程语言的形式：用类似编程语言的形式描述算法的过程，其中参杂使用一些数学符号和记号，用于描述算法中一些细节和具体操作
• 伪代码：类似于前一方式

三.算法的设计模式

　　*知道有这六种即可，我也没深入了解具体是什么怎么实现的，知道有这几种就行，遇到了再掌握吧！

　　*算法一般是多种模式的有机结合

四.算法的代价及度量

*首先明确，对于算法的研究，人们主要关注算法的最坏情况代价

　　1.时间代价(时间复杂度)

• 测定运行时间最可靠的方法就是计算对运行时间有消耗的基本操作的执行次数

举个栗子：对于同一个问题，算法A要做 2n+3 次操作、算法B要做 3n+1 次操作、算法c要做  2n^2+1 次操作，哪个算法好？？？

答：很明显随着n的增长(N趋近于无穷大)，总体来说 A<B<C

• 会用到"大O记法"（针对不同阶的表达式），定义什么的太麻烦了，直接简单的写步骤：

(要知道对于不同阶的表达式(比如  线性阶3n+10  平方阶2n^2  2n^2+3n+1) 随着n的增长(趋近于无穷大)，第二种算法趋近于第三种算法，而第1种算法远小于其余两种算法）

(因而得出结论 对于不同阶的表达式的比较 算法执行次数表达式的常数项和与最高次数相乘的常数乃至于次要项都不能起决定作用)

　　第一步：用常数1取代运行时间中的所有加法常数

　　第二步：再修改后的运算次数函数中，只保留最高阶项

　　第三步：如果最高阶项存在且不是1，则去除与这个项相乘的常数

• 下面列出常见的时间复杂度

执行次数函数举例	  阶	 非正式术语
12	         O(1)	    常数阶
2n+3	         O(n)	    线性阶
3n2+2n+1	 O(n2)	    平方阶
5log2n+20	 O(logn)    对数阶
2n+3nlog2n+19	 O(nlogn)   nlogn阶
6n3+2n2+3n+4	 O(n3)	    立方阶
2n	         O(2n)	    指数阶

#注意，经常将log₂n（以2为底的对数）简写成logn！！

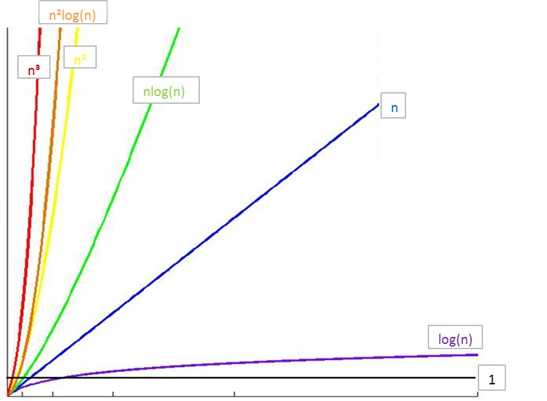
所消耗的时间从小到大

O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

我们举个栗子，推导下对数阶

count = 1
while count < n:
    count = count * 2 # 这行代码时间复杂度为O(1)

问：上述代码的时间复杂度为多少？

答：由于每次count*2后就会更接近于n，所以我们就要算 有多少个2相乘后大于n，使其退出循环。由2^x = n得到 x = logn.这个循环的时间复杂度为O(logn)

• 由于python程序是算法的实现，所以不得不考虑python程序的计算代价

 *有点懵 看不明白也没关系，我也看不明白，等学完用python语言程序实现后就自然而言明白了。

　　2.空间代价(空间复杂度)

 *时间复杂度指运行时间的需求，空间复杂度指空间需求。现目前，不必考虑。所以不准备怎么了解，先放放。

五.数据结构及分类

　　1.组成

• 数据：是描述客观事物的符号，是计算机可以操作的对象，是能被计算机识别并输出给计算机处理的符号集合
• 数据对象：是性质相同的数据元素的集合，在不混淆的情况下，数据=数据对象
• 数据元素：是组成数据的一定意义的基本单位，在计算机中通常作为整体处理
• 数据项：是数据不可分割的最小单位，一个数据元素可以由若干个数据项组成

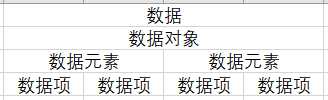
数据结构：是相互之间存在一种或者多种特定关系的数据元素的集合.由逻辑结构和物理结构.

　　2.逻辑结构

*逻辑结构是指数据对象中数据元素之间的相互关系

*逻辑结构包括：集合结构、序列结构(一对一)、层次结构、树形结构(一对多)、图结构(多对多)

　　3.物理结构

*物理结构是指数据的逻辑结构在计算机中的存储形式

• 顺序存储结构：把数据元素存放在地址连续的存储单元里
• 链式存储结构：把数据元素存放在任意的存储单元里，这组存储单元可以是连续的，也可以是不连续的

*那么我们不得不讨论下计算机内存对象的表示，以及python变量的引用语义

• 计算机内存对象表示

#内存是CPU可以直接访问的存储设备，与其对应的是外存(磁盘、光盘、磁带等)

#内存的基本结构是线性排列的一批存储单元(存储单元具有唯一的编号，称为单元地址或简称地址)。每个单元的大小相同，可以保存一个单位大小的数据.

举个例子：目前常见的64位操作系统，一次可以读取8个单元的数据，现在由一个float64的数据，我们可以得知float64 = 8字节 = 8个单元 = 64位二进制数

#当一个对象不再使用的时候，存储管理系统会设法回收其占用的存储，以便于用于存储其它对象

#对于一个组合对象，其中包含了一组元素，这些元素被安排到了一组连续的存储单元里，我们现在知道其起始地址位P，每个元素的大小相等为a，那么我们可以得知第K个元素的地址 loc(k) = p + k*a;

#还有一种情况，每个元素的大小不相等，那么我们就可以计算这类对象里的各个元素相对于起始地址的相对位置，称为元素的存储偏移量

• python变量的引用语义

#python语言是引用语义，C语言是值语义。简单来说，有一个值3.1415存储在内存的中，地址为p，那么 a = 3.1415,a变量里保存的是p，同样的我们再把3.1415赋值给b，b变量里保存的同样是p，a和b的同时指向了3.1415这一数据所在的地址，即a和b变量的存储区里保存的都是p。而C语言是吧变量的值直接保存在变量的存储区里。

0.数据结构(python语言) 基本概念 算法的代价及度量！！！

标签：一对多   数据结构   image   nlogn   输入参数   ima   3.1   存储管理   内存   

原文地址：https://www.cnblogs.com/DC0307/p/10681663.html