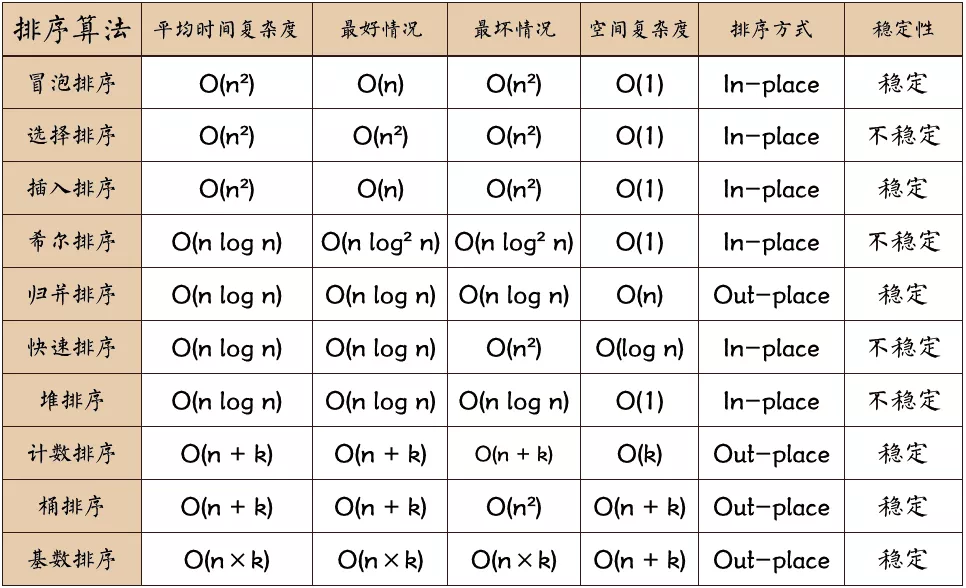
标签:sub 增量 思想 swap 归并排序 位置 相等 == 桶排序
目录

def bubble_sort(arr):
'''
如果没有逆序对,提前退出循环
'''
n = len(arr)
for i in range(n-1):
swapped = False
for j in range(n-1-i):
if arr[j] > arr[j+1]:
arr[j],arr[j+1] = arr[j+1],arr[j]
swapped = True
# print(arr)
if not swapped:
break
return arr
def selection_sort(arr):
n = len(arr)
for i in range(n):
min = i
for j in range(i+1, n):
if arr[j] < arr[min]:
min = j
arr[i],arr[min] = arr[min],arr[i]
# print(arr)
return arr
def insertion_sort(arr):
n = len(arr)
for i in range(n):
cursor = arr[i]
pos = i
while pos > 0 and arr[pos-1] > cursor:
# 大于cursor就一直往前移,前面的数往后补位
arr[pos] = arr[pos-1]
pos = pos-1
# 最后再赋值
arr[pos] = cursor
# print(arr)
return arr希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:

def shell_sort(arr):
'''
相当于套了一个gap的插入排序:每次排序的对象是数组中间隔gap的元素
'''
n = len(arr)
gap = n//2
while gap > 0: # gap=0是循环出口
for i in range(gap, n):
cursor = arr[i]
pos = i
while pos >= gap and arr[pos-gap] > cursor:
arr[pos] = arr[pos-gap]
pos -= gap
arr[pos] = cursor
# print(arr)
gap = gap//2
return arr
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr)//2
left,right = arr[:mid],arr[mid:]
return merge(merge_sort(left), merge_sort(right), arr.copy())
def merge(left, right, merged):
l,r = 0,0
while l < len(left) and r < len(right):
if left[l] <= right[r]:
merged[l+r] = left[l]
l+=1
else:
merged[l+r] = right[r]
r+=1
for l in range(l, len(left)): # 注意这里的l和r
merged[l+r] = left[l]
for r in range(r, len(right)):
merged[l+r] = right[r]
return merged快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。

def partition(arr, low, high):
i = low-1 # i是小于pivot的数的索引
pivot = arr[high]
for j in range(low, high):
# 遍历low到high,将所有小于pivot的数都提到前面来
if arr[j] < pivot:
i += 1
arr[i],arr[j]=arr[j],arr[i]
# 将pivot提到索引i之后
arr[i+1],arr[high]=arr[high],arr[i+1]
return (i+1)
def quick_sort(arr, low, high):
if low < high:
pivot = partition(arr, low, high)
quick_sort(arr, low, pivot-1)
quick_sort(arr, pivot+1, high)
return arr
########################################
def qsort(arr):
'''
简化版,利用了python list的特点
速度很慢,严格意义上不算快排
'''
if len(arr) <= 1:
return arr
pivot = arr[-1]
return qsort([x for x in arr[:-1] if x < pivot]) + [pivot] + qsort([x for x in arr[:-1] if x >= pivot])heapify(),目的是把新的数组顶端数据调整到相应位置;
def heapify(arr, n, i):
largest = i
l = 2 * i + 1
r = 2 * i + 2
# arr = [1,2,3,6,4,3,7,8,13,5]
# print(" {} ".format(arr[0]))
# print(" {} {} ".format(arr[1], arr[2]))
# print(" {} {} {} {} ".format(arr[3],arr[4],arr[5],arr[6]))
# print("{} {} {} ".format(arr[7],arr[8],arr[9]))
# print("==========================")
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i],arr[largest] = arr[largest],arr[i]
heapify(arr, n, largest)
def heap_sort(arr):
n = len(arr)
# 建立大顶堆:从 n//2-1 逐渐往顶部走
for i in range(n//2-1, -1, -1):
heapify(arr, n, i)
# 排序
for i in range(n-1, 0, -1):
# 交换顶部与末端未排序元素
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
return arr计数排序是一种非基于比较的排序算法,其空间复杂度和时间复杂度均为O(n+k),其中k是整数的范围。
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
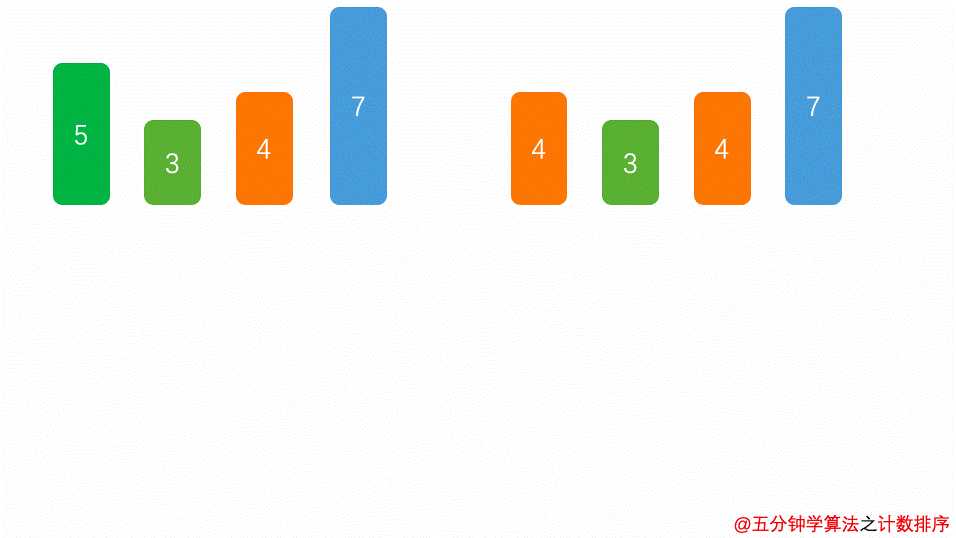
def counting_sort(arr):
m = min(arr)
# 对负数设置一个offset
offset = 0
if m < 0:
offset = -m
for i in range(len(arr)):
arr[i] += offset
k = max(arr)
temp_arr = [0] * (k + 1)
for i in range(0, len(arr)):
temp_arr[arr[i]] += 1
for i in range(1, k + 1):
# 向后叠加
temp_arr[i] += temp_arr[i - 1]
result_arr = arr.copy()
for i in range(len(arr) - 1, -1, -1):
# arr[i]的排位看temp_arr[arr[i]]的数值,并减一(自身)
result_arr[temp_arr[arr[i]] - 1] = arr[i] - offset
# 针对重复位情况
temp_arr[arr[i]] -= 1
return result_arr桶排序(Bucket sort)是一种基于计数的排序算法。

def bucket_sort(arr, bucket_size=5):
min_value,max_value = min(arr),max(arr)
bucket_count = (max_value-min_value)//bucket_size + 1
buckets = [[] for _ in range(bucket_count)]
for i in arr:
buckets[(i-min_value)//bucket_size].append(i)
sorted_list = []
for bucket in buckets:
sorted_list.extend(next_sort(bucket))
return sorted_list
def next_sort(arr):
# 插入排序
n = len(arr)
for i in range(n):
cursor = arr[i]
pos = i
while pos>0 and arr[pos-1]>cursor:
arr[pos] = arr[pos-1]
pos -= 1
arr[pos] = cursor
return arr
def radix_sort(arr):
'''
先按个位排,再按十位排...直到pos>max
'''
pos = 1
max_value = max(arr)
while pos<max_value:
queue_list = [list() for _ in range(10)]
for num in arr:
digit_number = num // pos % 10
queue_list[digit_number].append(num)
index = 0
for numbers in queue_list:
for num in numbers:
arr[index] = num
index += 1
pos*=10
return arr标签:sub 增量 思想 swap 归并排序 位置 相等 == 桶排序
原文地址:https://www.cnblogs.com/southtonorth/p/12287415.html