标签:string 有一个 save build 替换 改变 color 没有 实现
//打印树
#ifndef DRAWTREE_HH
#define DRAWTREE_HH
#include <ostream>
#include <sstream>
#include <iostream>
#include <cmath>
#include <algorithm>
namespace DrawTree
{
#define lChild left //使用前将 l_child_ 更换为 自己树节点的左孩子的名字
#define rChild right //使用前将 r_child_ 更换为 自己树节点的右孩子的名字
#define MAXN (1000) //这棵树的节点上限
#define PERID (2) //打印两个节点的横坐标间隔
int SUM; //统计当前遍历到第几个节点
// 将光标移动到 (X,Y)
std::string AXIS(int X, int Y) {
std::stringstream ss;
ss << "\033[" << Y << ";" << X << "H";
return ss.str();
}
struct DrawNode {
int x, y, dataSize;
}axisArray[MAXN];
//计算节点数据输出的长度
template <typename TreePtr>
int dataSize(TreePtr const& root) {
std::stringstream ss;
//对应buildDrawTree中的打印,对应树结点的数据
ss << root->data << "/" << root->color;
return (ss.str()).length();
}
//中序遍历, 从左往右画节点(不连线)
//横坐标通过全局变量SUM和上一个节点数据的输出长度算出
//纵坐标通过递归深度判断
//PERID 是两个节点间隔长度
template <typename TreePtr>
void buildDrawTree(TreePtr const& root, int deep) {
if (!root) return; //判断空节点,如果你的节点判空和我不一样,这里也要改, 比如我之前的判断空节点是(root->height_== -1).
if (root->lChild) buildDrawTree(root->lChild, deep + 1);
axisArray[SUM] = { axisArray[SUM - 1].x + axisArray[SUM - 1].dataSize + PERID, deep, dataSize(root) };
std::cout << AXIS(axisArray[SUM].x, axisArray[SUM].y) << root->data << "/" << root->color;
++SUM;
if (root->rChild) buildDrawTree(root->rChild, deep + 1);
}
template <typename TreePtr>
void Draw(TreePtr const& t) { //画树函数
system("cls"); //清屏
SUM = 1;
int maxy = 0;
buildDrawTree<TreePtr>(t, 2); //每个结点画出来
//画节点间连线,因为画的节点不会太多,所以就写了n^2的算法,比较好实现
//每个节点只有一个父节点,所以画出每个节点和自己父节点的连线即可
for (int i = 1; i < SUM; i++) {
//x,y是子节点的坐标,p是父节点的axisArray数组的下标, px,py是父节点的坐标;
int x = axisArray[i].x, y = axisArray[i].y, p = 0, px = 0, py = y - 1;
if (y == 1) continue; // 根结点没有父节点,跳过
for (int j = 1; j < SUM; j++) { //循环找父节点
if (i == j) continue;
if ((!p || abs(axisArray[j].x - x) < abs(px - x)) && axisArray[j].y + 1 == y)
p = j, px = axisArray[j].x;
}
int s = (2 * x + axisArray[i].dataSize) >> 1;
std::cout << AXIS(s, py) << ‘+‘;
if (s < px)
for (int i = s + 1; i < px; i++) std::cout << AXIS(i, py) << ‘-‘;
else
for (int i = px + axisArray[p].dataSize; i < s; i++) std::cout << AXIS(i, py) << ‘-‘;
maxy = std::max(maxy, y);
}
std::cout << AXIS(1, maxy + 1); //打印完把光标移到最下边.
}
}
#endif
#include <iostream>
#include <vector>
#include "DrawATree.h"
using namespace std;
struct treeNode {
int data;
enum c { RED, BLACK };
c color;
treeNode* left, * right, * parent;
};
//根
treeNode* pRoot;
//叶子节点,全局共用
treeNode leaf;
treeNode* leafNode = &leaf;
//LL型,右旋单旋
//和AVL差不多,主要是多了parent之间的更新
//画图更容易判断
void LL(treeNode* curr) {
treeNode* leftNode = curr->left;
curr->left = leftNode->right;
if(leftNode->right != leafNode) leftNode->right->parent = curr;
leftNode->parent = curr->parent;
//注意如果对根节点进行旋转的话要更新根节点
if (curr == pRoot) {
pRoot = leftNode;
pRoot->parent = nullptr;
}
else if (curr->parent->right == curr) curr->parent->right = leftNode;
else curr->parent->left = leftNode;
curr->parent = leftNode;
leftNode->right = curr;
}
//RR型,左旋单旋
void RR(treeNode* curr) {
treeNode* rightNode = curr->right;
curr->right = rightNode->left;
if (rightNode->left != leafNode) rightNode->left->parent = curr;
rightNode->parent = curr->parent;
if (curr == pRoot) {
pRoot = rightNode;
pRoot->parent = nullptr;
}
else if (curr->parent->left == curr) curr->parent->left = rightNode;
else curr->parent->right = rightNode;
curr->parent = rightNode;
rightNode->left = curr;
}
//插入后重平衡
//判断是否需要重平衡有三种条件
//重平衡分三种
//要保持子孙路径的黑色节点个数一样和红色节点的子节点不能为红色节点
//画图更容易判断
void insertRebalance(treeNode* curr) {
//迭代,①curr为根节点或者②curr的父节点为黑色无需重平衡
//需要重平衡只有③curr的父节点为红色的情况
while (curr != pRoot && curr->parent->color == treeNode::RED) {
//找uncle结点,需要分两种
if (curr->parent->parent->left == curr->parent) {
treeNode* uncle = curr->parent->parent->right;
//uncle为黑色,curr为左节点
if (uncle->color == treeNode::BLACK
&& curr->parent->left == curr) {
curr->parent->color = treeNode::BLACK;
curr->parent->parent->color = treeNode::RED;
LL(curr->parent->parent);
}
//uncle为黑色,curr为右节点
//完成后变为curr为左节点的情况,迭代进行
else if (uncle->color == treeNode::BLACK
&& curr->parent->right == curr) {
curr = curr->parent;
RR(curr);
}
//uncle为红色
else if (uncle->color == treeNode::RED) {
curr->parent->color = treeNode::BLACK;
uncle->color = treeNode::BLACK;
curr->parent->parent->color = treeNode::RED;
curr = curr->parent->parent;
}
}
//和上面以此类推
else if (curr->parent->parent->right == curr->parent) {
treeNode* uncle = curr->parent->parent->left;
if (uncle->color == treeNode::BLACK
&& curr->parent->left == curr) {
curr = curr->parent;
LL(curr);
}
else if (uncle->color == treeNode::BLACK
&& curr->parent->right == curr) {
curr->parent->color = treeNode::BLACK;
curr->parent->parent->color = treeNode::RED;
RR(curr->parent->parent);
}
else if (uncle->color == treeNode::RED) {
curr->parent->color = treeNode::BLACK;
uncle->color = treeNode::BLACK;
curr->parent->parent->color = treeNode::RED;
curr = curr->parent->parent;
}
}
}
//将根节点标为黑色,有两种条件会迭代回到根节点而结束
pRoot->color = treeNode::BLACK;
}
//插入结点
void insert(int num) {
treeNode* prev = pRoot, *curr = pRoot;
//如果找到了叶子结点的位置,分配空间
while (curr != leafNode) {
prev = curr;
//如果数字比当前节点的值小,即进入当前节点的左子树继续判断
if (num < curr->data) curr = curr->left;
//如果数字比当前节点的值大,即进入当前节点的右子树继续判断
else if (num > curr->data) curr = curr->right;
else if (curr->data == num) return;
}
//建一个新结点,红色
treeNode* newNode = new treeNode();
newNode->color = treeNode::RED;
newNode->parent = prev;
newNode->left = newNode->right = leafNode;
newNode->data = num;
//如果树还没建立,则新结点为根节点
//insertRebalance会把根节点标为黑色,parent要指回自己
if (curr == pRoot) {
pRoot = newNode;
pRoot->parent = nullptr;
insertRebalance(pRoot);
}
//因为不是传引用,所以要借用prev才能改变树
else if (num < prev->data) {
prev->left = newNode;
insertRebalance(prev->left);
}
else if (num > prev->data) {
prev->right = newNode;
insertRebalance(prev->right);
}
}
//1. 节点是红色
//2. 节点是黑色
//3. 节点为根节点
//删除后重平衡
void deleRebalance(treeNode* curr) {
//1、3跳出循环
//2节点是黑色进入循环
while (curr->color == treeNode::BLACK && curr != pRoot) {
//2.1 节点是父节点的左子节点
if (curr->parent->left == curr) {
treeNode* brother = curr->parent->right;
//2.1.2 节点的兄弟节点是黑色
//2.1.2.1 节点的兄弟节点有右子节点
if (brother->color == treeNode::BLACK
&& brother->left == leafNode && brother->right != leafNode) {
brother->color = curr->parent->color;
brother->right->color = treeNode::BLACK;
curr->parent->color = treeNode::BLACK;
RR(curr->parent);
break;
}
//2.1.2.2 节点的兄弟节点有左子节点
else if (brother->color == treeNode::BLACK
&& brother->left != leafNode && brother->right == leafNode) {
brother->left->color = treeNode::BLACK;
brother->color = treeNode::RED;
LL(brother);
//循环回到2.1.2.1
}
//2.1.2.3 节点的兄弟节点有左右子节点
else if (brother->color == treeNode::BLACK
&& brother->left != leafNode && brother->right != leafNode) {
brother->color = curr->parent->color;
brother->right->color = treeNode::BLACK;
curr->parent->color = treeNode::BLACK;
RR(curr->parent);
break;
}
//2.1.2.4 节点的兄弟节点为叶子节点
else if (brother->color == treeNode::BLACK
&& brother->left == leafNode && brother->right == leafNode) {
brother->color = treeNode::RED;
curr = curr->parent;
}
//2.1.3 节点的兄弟节点是红色
else if (brother->color == treeNode::RED) {
brother->left->color = treeNode::RED;
brother->color = treeNode::BLACK;
RR(curr->parent);
break;
}
}
//2.2 节点是父节点的右子节点
else if (curr->parent->right == curr) {
treeNode* brother = curr->parent->left;
//2.1.2.1 节点的兄弟节点有左子节点
if (brother->color == treeNode::BLACK
&& brother->left != leafNode && brother->right == leafNode) {
brother->color = curr->parent->color;
brother->left->color = treeNode::BLACK;
curr->parent->color = treeNode::BLACK;
LL(curr->parent);
break;
}
//2.1.2.1 节点的兄弟节点有右子节点
else if (brother->color == treeNode::BLACK
&& brother->left == leafNode && brother->right != leafNode) {
brother->right->color = treeNode::BLACK;
brother->color = treeNode::RED;
RR(brother);
//循环回到2.2.2.1
}
//2.2.2.3 节点的兄弟节点有左右子节点
else if (brother->color == treeNode::BLACK
&& brother->left != leafNode && brother->right != leafNode) {
brother->color = curr->parent->color;
brother->left->color = treeNode::BLACK;
curr->parent->color = treeNode::BLACK;
LL(curr->parent);
break;
}
//2.2.2.4 节点的兄弟节点为叶子节点
else if (brother->color == treeNode::BLACK
&& brother->left == leafNode && brother->right == leafNode) {
brother->color = treeNode::RED;
curr = curr->parent;
}
//2.2.3 节点的兄弟节点是红色
else if (brother->color == treeNode::RED) {
brother->right->color = treeNode::RED;
brother->color = treeNode::BLACK;
LL(curr->parent);
break;
}
}
}
//循环里2.1.2.4和2.2.2.4需要找到红节点标为黑色
curr->color = treeNode::BLACK;
}
//删除节点
void dele(int num) {
treeNode* curr = pRoot;
while (curr != leafNode) {
//如果数字比当前节点的值小,即进入当前节点的左子树继续判断
if (num < curr->data) curr = curr->left;
//如果数字比当前节点的值大,即进入当前节点的右子树继续判断
else if (num > curr->data) curr = curr->right;
else if (curr->data == num) {
//当前结点为根节点
if (curr == pRoot) {
//根节点为叶子节点
if (curr->left == leafNode && curr->right == leafNode) {
pRoot = leafNode;
delete curr;
curr = nullptr;
}
//根节点有右结点
else if (curr->left == leafNode && curr->right != leafNode) {
pRoot = curr->right;
curr->right->parent = nullptr;
curr->right->color = treeNode::BLACK;
delete curr;
curr = nullptr;
}
//根节点有左节点
else if (curr->left != leafNode && curr->right == leafNode) {
pRoot = curr->left;
curr->left->parent = nullptr;
curr->left->color = treeNode::BLACK;
delete curr;
curr = nullptr;
}
//根节点有左右节点
else if (curr->left != leafNode && curr->right != leafNode) {
//找到后继结点
auto save = curr->right;
while (save->left != leafNode) save = save->left;
//记录前驱结点的值,再往下递归找前驱结点(一定是一个叶子节点)
//必须这样做,不可以删除直接删除前驱结点,因为回溯时要进行重平衡
int value = save->data;
dele(value);
curr->data = value;
}
}
//当前节点为左节点
else if (curr->parent->left == curr) {
//当前节点为叶子节点且为红色
if (curr->left == leafNode && curr->right == leafNode
&& curr->color == treeNode::RED) {
curr->parent->left = leafNode;
delete curr;
curr = nullptr;
}
//当前节点为叶子节点且为黑色
else if (curr->left == leafNode && curr->right == leafNode
&& curr->color == treeNode::BLACK) {
deleRebalance(curr);
curr->parent->left = leafNode;
delete curr;
curr = nullptr;
}
//当前节点有右结点
else if (curr->left == leafNode && curr->right != leafNode) {
curr->parent->left = curr->right;
curr->right->parent = curr->parent;
curr->right->color = treeNode::BLACK;
delete curr;
curr = nullptr;
}
//当前节点有左节点
else if (curr->left != leafNode && curr->right == leafNode) {
curr->parent->left = curr->left;
curr->left->parent = curr->parent;
curr->left->color = treeNode::BLACK;
delete curr;
curr = nullptr;
}
//当前节点有左右节点
else if (curr->left != leafNode && curr->right != leafNode) {
//找到后继结点
auto save = curr->right;
while (save->left != leafNode) save = save->left;
//记录前驱结点的值,再往下递归找前驱结点(一定是一个叶子节点)
//必须这样做,不可以删除直接删除前驱结点,因为回溯时要进行重平衡
int value = save->data;
dele(value);
curr->data = value;
}
}
//当前节点为右节点
else if (curr->parent->right == curr) {
//当前节点为叶子节点且为红色
if (curr->left == leafNode && curr->right == leafNode
&& curr->color == treeNode::RED) {
curr->parent->right = leafNode;
delete curr;
curr = nullptr;
}
//当前节点为叶子节点且为黑色
else if (curr->left == leafNode && curr->right == leafNode
&& curr->color == treeNode::BLACK) {
deleRebalance(curr);
curr->parent->right = leafNode;
delete curr;
curr = nullptr;
}
//当前节点有右结点
else if (curr->left == leafNode && curr->right != leafNode) {
curr->parent->right = curr->right;
curr->right->parent = curr->parent;
curr->right->color = treeNode::BLACK;
delete curr;
curr = nullptr;
}
//当前节点有左节点
else if (curr->left != leafNode && curr->right == leafNode) {
curr->parent->right = curr->left;
curr->left->parent = curr->parent;
curr->left->color = treeNode::BLACK;
delete curr;
curr = nullptr;
}
//当前节点有左右节点
else if (curr->left != leafNode && curr->right != leafNode) {
//找到后继结点
auto save = curr->right;
while (save->left != leafNode) save = save->left;
//记录前驱结点的值,再往下递归找前驱结点(一定是一个叶子节点)
//必须这样做,不可以删除直接删除前驱结点,因为回溯时要进行重平衡
int value = save->data;
dele(value);
curr->data = value;
}
}
break;
}
}
}
//建树
void createTree(vector<int> v) {
for (int i = 0; i < static_cast<int>(v.size()); i++) {
insert(v[i]);
DrawTree::Draw(pRoot);
}
}
int main() {
vector<int> v = { 49,38,65,97,76,13,27,100 };
//构造叶子节点,所有叶子节点都用这个
leafNode->left = leafNode->right = leafNode->parent = nullptr;
leafNode->color = treeNode::BLACK;
leafNode->data = -1;
//初始化根节点为叶子节点
pRoot = leafNode;
createTree(v);
DrawTree::Draw(pRoot);
int num;
string action;
while (true) {
cout << "删除/添加/退出(d/a/z): ";
cin >> action;
if (action == "d") {
cin >> num;
dele(num);
}
else if (action == "a") {
cin >> num;
insert(num);
}
else if (action == "z") break;
DrawTree::Draw(pRoot);
}
return 0;
}
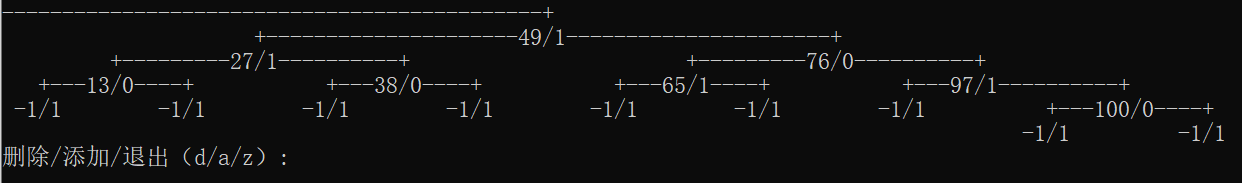
标签:string 有一个 save build 替换 改变 color 没有 实现
原文地址:https://www.cnblogs.com/wasi-991017/p/14444248.html