零零散散学算法之具体解释几种最短路径

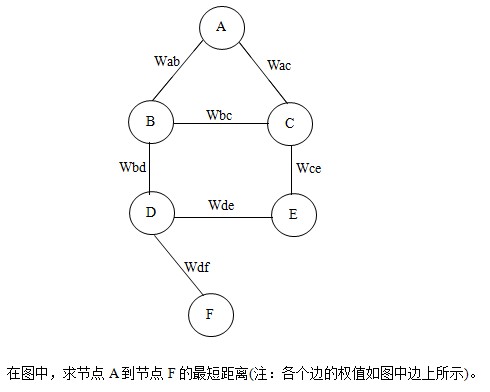
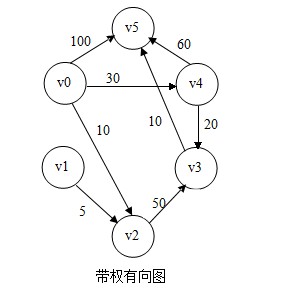
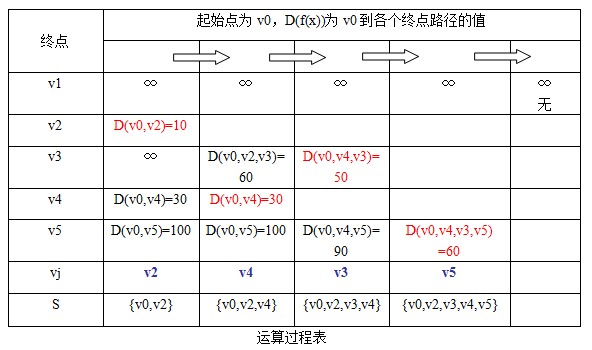
int ShortPath(MGraph G,int v0,PathMatrix &P,ShortPathTable &D)
{
	//用戴克斯特拉算法求有向图G中v0顶点到其余顶点v的最短路径P[v]及带权长度D[v]。
	//若P[v][w]为TRUE,则w是从v0到v当前求得最短路径上的顶点。
	//final[v]为TRUE当且仅当v∈S,即已经求得从v0到v的最短路径。
	
	for(v = 0;v < G.vexmun;v++)
	{
		final[v] = FALSE;
		D[v] = G.WeiArcs[v0][v];
		for(w = 0;w < G.vexnum;w++)
			P[v][w] = FALSE;	//设空路径
		if(D[v] < INFINITY)
		{
			p[v][v0] = TRUE;
			p[v][v] = TRUE;
		}
	}
	
	D[v0] = 0;final[v0] = TRUE;	//初始化，v0顶点属于S集合
	
	//開始主循环，每次求得v0到某个顶点v的最短路径，并将v加到S集合中
	for(i = 1; i < G.vexnum; i++)	//其余G.vexnum - 1个顶点
	{
		min = INFINITY;	//当前所知离v0点的近期距离
		for(w = 0;w < G.vexnum; i++)
		{
			if(!final[w])	//w顶点在V - S中
			{
				if(D[w] < min)	//w顶点离v0更近
				{
					v = w;
					min = D[w];
				}
			}
		}
		final[v] = TRUE;	//离v0顶点近期的v增加到S中
		
		for(w = 0;w < G.vexnum;w++)	//更新当前最算路径及距离
		{
			if(!final[w] && (min + G.WeiArcs < D[w]))
			{
				D[w] = min + G.WeiArcs[v][w];
				//p[w] = P[v] + P[w];
				P[w] = P[v];
				P[w][w] = TRUE;
			}
		}
	}
	return 0;
}

求解的过程见下图：

上述过程描写叙述的弗洛伊德算法的代码例如以下：

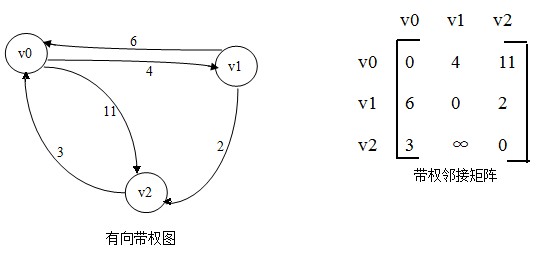
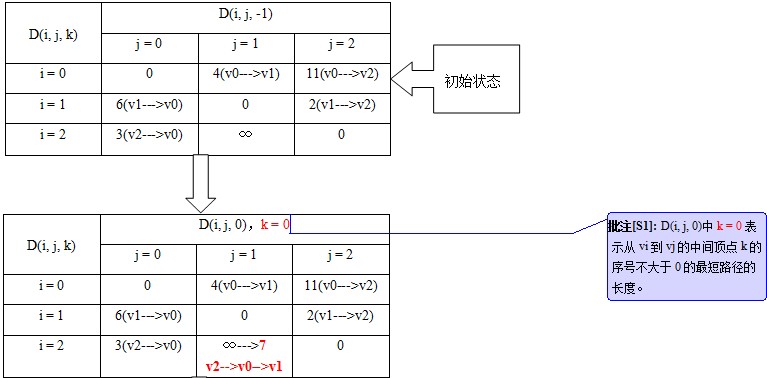
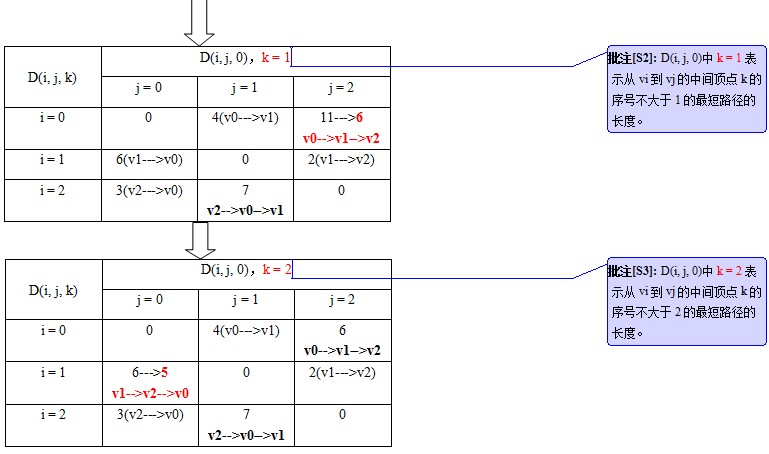
int ShortPath(MGraph G,int v0,PathMatrix &P,ShortPathTable &D)
{
	//用Floyd算法求有向图中各对顶点v和w之间的最短路径P[v][w]及其带权长度D[v][w]。
	//若p[v][w][u]为TRUE,则u是从v到w当前求得的最短路径上的顶点
	for(v = 0;v < G.vexnum;v++)
		for(w = 0;w < G.vexnum;w++)
		{
			D[v][w] = G.arcs[v][w];
			if(D[v][w] < INFINITY)	//从v到w有直接路径
			{
				P[v][w][u] = TRUE;
				P[v][w][w] = TRUE;
			}
		}
		
	for(u = 0;u < G.vexnum;u++)
		for(v = 0;v < G.vexnum;v++)
			for(w = 0;w < G.vexnum;w++)
			{
				if(D[v][u] + D[u][w] < D[v][w])	//从v经u到w的一条更短路径
					D[v][w] = D[v][u] < D[u][w];
				for(i = 0;i < G.vexnum;i++)
					P[v][w][i] = P[v][u][i] || P[u][w][i];
			}
	return 0;
}

第四节 A*搜索算法
       A*搜索算法，俗称A星算法。这是一种在图平面上，有多个节点的路径，求出最低通过成本的算法。经常使用于游戏中的NPC的移动计算，或线上游戏的BOT的移动计算上。该算法像Dijkstra算法一样，能够找到一条最短路径；也像BFS一样，进行启示式的搜索。

       A*算法最核心的部分，就在于它的一个估值函数的设计上：f(n)=g(n)+h(n)。当中，g(n)表示从起始点到任一点n的实际距离，h(n)表示随意顶点n到目标顶点的估算距离，f(n)是每一个可能试探点的估值。这个估值函数遵循下面特性：
       ?假设h(n)为0，仅仅需求出g(n)，即求出起点到随意顶点n的最短路径，则转化为单源最短路径问题，即Dijkstra算法；
       ?假设h(n)<=“n到目标的实际距离”，则一定能够求出最优解。并且h(n)越小，须要计算的节点越多，算法效率越低。

       我们能够这样来描写叙述：从出发点(StartPoint,缩写成sp)到终点(EndPoint，缩写成ep)的最短距离是一定的，于是我们能够写一个估值函数来预计出发点到终点的最短距离。假设程序尝试着从出发点沿着某条线路移动到了路径上的还有一个点（Otherpoint,缩写成op），那么我们觉得这个方法所得到的从sp到ep间的预计距离为：从sp到op实际已走的距离加上预计函数估出的从op到ep的距离。如此，不管我们的程序搜索展开到哪一步，都会得到一个预计值，每一次决策后，将评估值和等待处理的方案一起排序，然后挑出待处理的各个方案中最有可能是最短路线的一部分的方案展开到下一步, 一直循环直到对象移动到目的地，或全部方案都尝试过，却没有找到一条通向目的地的路径则结束。

A*搜索算法的图解过程请看：http://blog.vckbase.com/panic/archive/2005/03/20/3778.html

第五节 相关说明
參考资料：数据结构(严蔚敏)、维基百科之A*搜索算法

第六节 结束语
      想想，写写，画画......