标签:
题目要求:
返回一维数组中最大子数组的和
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
如果数组A[0]……A[j-1]首尾相邻,允许A[i-1], …… A[n-1], A[0]……A[j-1]之和最大。
同时返回最大子数组的位置。
求所有子数组的和的最大值。
要求时间复杂度为O(n)
设计思路:(结对思考以及参考于其他同学)
考虑到数组需要首尾相连,采取把数组的长度增加两倍,并把复制的数组写在在最后一个数的后面,这样在循环的过程中并不需要采用新的算法,只要把原来的代码稍微修改一下,加一个判断使得组成最大数组的长度不超过原数组的长度即可。
程序源代码:
#include <iostream.h>
#include <stdlib.h>
int main()
{
int num,length,start,finish;
start=0;
finish=0;
cout<<"请输入数组元素个数:";
cin>>length;
num=2*length; //分配2倍数组空间,方便下次比较
int* Array=new int[num]; //分配数组空间
for(int i=0;i<length;i++) //数组正负交替出现
{
if(i%2==0)
Array[i]=rand()%1000;
else
Array[i]=0-(rand()%1000);
}
cout<<"数组为:";
for(i=0;i<length;i++)
{
cout<<Array[i]<<" ";
}
cout<<endl;
//以下代码参考与其他同学以及度娘
int max=Array[0];
int sum=0; //定义求和变量
for(i=0;i<length;i++)
{
sum=0;
for(int j=i;j<length+i;j++)
{
sum=sum+Array[j];
if(sum>max)
{
max=sum;
start=i;
finish=j;
}
}
Array[length+i]=Array[i]; //每次将已经计算过的数放到最后
}
if(finish>=length)
{
cout<<"最大子数组起始位置为:"<<start+1<<endl;
cout<<"最大子数组终止位置为:"<<finish-length+1<<endl;
}
else
{
cout<<"最大子数组起始位置为:"<<start+1<<endl;
cout<<"最大子数组终止位置为:"<<finish+1<<endl;
}
cout<<"最大子数组为:"<<endl;
for(int m=start;m<=finish;m++)
{
cout<<Array[m]<<" ";
}
cout<<endl;
cout<<"最大子数组的和为:"<<endl;
cout<<max<<endl;
delete []Array;
return 0;
}
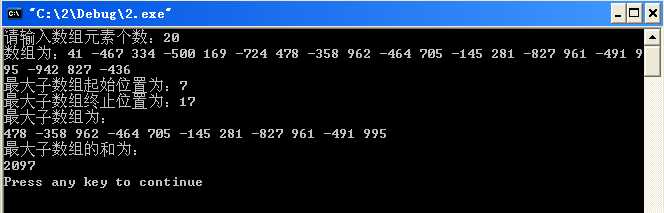
运行结果截图:
本对照片:
太菜了,还是低调一点吧。
实验总结:
这个题我不会解,所以发的晚。最后参考其他大神同学的代码,并且充分的理解了其解题精髓。今后还要好好提高自己的能力,太菜了。
标签:
原文地址:http://www.cnblogs.com/duang/p/4379075.html