hdu 4568 spfa 最短路算法+旅行商问题

标签：

http://acm.hdu.edu.cn/showproblem.php?pid=4568

　　One day, a hunter named James went to a mysterious area to find the treasures. James wanted to research the area and brought all treasures that he could.
　　The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can‘t cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can‘t remember whether the point are researched or not).
　　Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.

2
3 3
3 2 3
5 4 3
1 4 2
1
1 1
3 3
3 2 3
5 4 3
1 4 2
2
1 1
2 2

8
11

/**
hdu 4568 spfa 最短路算法+旅行商问题
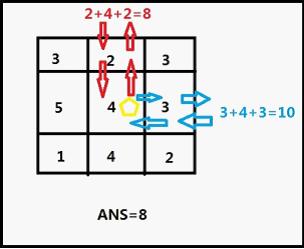
题目大意：给定一个n*m的棋盘，每一个格子有一个值，代表经过这个格子的花费，给出sum个宝藏点的坐标，求从棋盘的任意一个边进入棋盘，经过所有的宝藏点后在走出
          棋盘所需要的最小花费
解题思路：spfa处理处任意两个宝藏点之间的最短距离（最小花费）和每个宝藏点和边界的最短距离。然后状态压缩：dp[s][i]表示经过宝藏点的状态为s并且结尾点为i的
          最小花费
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#include <queue>
using namespace std;
const int maxn=205;
int n,m;
struct note
{
    int x,y;
} point[15];

int dx[4][2]= {1,0,0,1,-1,0,0,-1};
int dis[maxn][maxn],a[maxn][maxn],dis_border[25],length[20][20];
bool vis[maxn][maxn];
int dp[1<<15][15];

void spfa(int s)
{
    for(int i=0;i<n;i++)
         for(int j=0;j<m;j++)
            dis[i][j]=0x3f3f3f3f;
    memset(vis,0,sizeof(vis));
    queue<pair<int,int> >q;
    q.push(make_pair(point[s].x,point[s].y));
    vis[point[s].x][point[s].y]=1;
    dis[point[s].x][point[s].y]=0;
    while(!q.empty())
    {
        int x=q.front().first;
        int y=q.front().second;
        q.pop();
        vis[x][y]=0;
        if(x==0||x==n-1||y==0||y==m-1)
            dis_border[s]=min(dis_border[s],dis[x][y]);
        for(int i=0; i<4; i++)
        {
            int xx=x+dx[i][0];
            int yy=y+dx[i][1];
            if(xx>=0&&xx<n&&yy>=0&&yy<m&&a[xx][yy]!=-1)
            {
                if(dis[xx][yy]>dis[x][y]+a[xx][yy])
                {
                    dis[xx][yy]=dis[x][y]+a[xx][yy];
                    if(vis[xx][yy]==0)
                    {
                        vis[xx][yy]=1;
                        q.push(make_pair(xx,yy));
                    }
                }
            }
        }
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<m; j++)
            {
                scanf("%d",&a[i][j]);
            }
        }
        int k;
        scanf("%d\n",&k);
        for(int i=0;i<k;i++)
        {
            scanf("%d%d",&point[i].x,&point[i].y);
        }
        //===预处理===
        for(int i=0;i<k;i++)
        {
            dis_border[i]=0x3f3f3f3f;
            for(int j=0;j<k;j++)
            {
                if(i==j)
                    length[i][j]=0;
                else
                    length[i][j]=0x3f3f3f3f;
            }
        }
        for(int i=0;i<(1<<k);i++)
        {
            for(int j=0;j<k;j++)
            {
                dp[i][j]=0x3f3f3f3f;
            }
        }
        //===求有宝藏的点之间和每一个宝藏点和边界的最短距离===
        for(int i=0; i<k; i++)
        {
            spfa(i);
            for(int j=0; j<k; j++)
            {
                if(j==i)continue;
                length[i][j]=min(dis[point[j].x][point[j].y],length[i][j]);
            }
            dp[1<<i][i]=dis_border[i]+a[point[i].x][point[i].y];
        }
        ///===求最优路径===
        for(int s=0;s<(1<<k);s++)
        {
            for(int i=0;i<k;i++)
            {
                if(s&(1<<i)==0)continue;
                if(dp[s][i]==0x3f3f3f3f)continue;
                for(int j=0;j<k;j++)
                {
                    if(s&(1<<j)==1)continue;
                    dp[s|(1<<j)][j]=min(dp[s|(1<<j)][j],dp[s][i]+length[i][j]);
                }
            }
        }
        ///===还要回到边界==
        int ans=0x3f3f3f3f;
        for(int i=0;i<k;i++)
        {
            ans=min(ans,dp[(1<<k)-1][i]+dis_border[i]);
        }
        printf("%d\n",ans);
    }
    return 0;
}

hdu 4568 spfa 最短路算法+旅行商问题

标签：

原文地址：http://blog.csdn.net/lvshubao1314/article/details/45845419