标签:
这一次,笔者使用了STL库中的优先级队列(Priority Queue)来完成Dijkstra算法中extract-min()语句(即从未选中的节点中选取一个距离原点s最小的点)的功能。由于优先级队列的插入、删除操作只需要logn的时间花费,因此降低了不少运行时间。
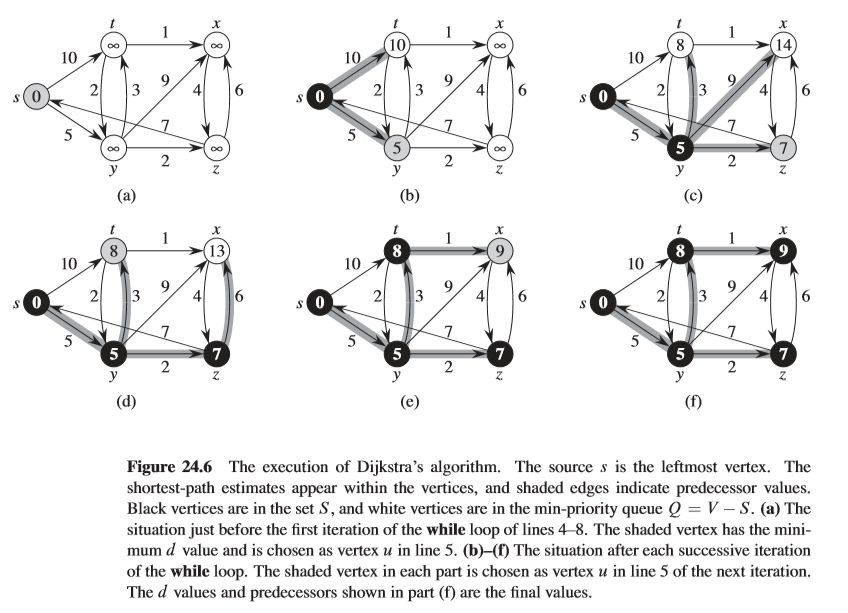
本文使用C++实现了这一基本算法。参考《算法导论》第24.3节。
/**
* Dijkstra‘s Single Source Shortest Path Algorithm in C++
* Time Cost : O(MlogN)
* Thanks to Introduction to Algorithms (CLRS) Chapter 24.3
* Author: Zheng Chen / Arclabs001
* Copyright 2015 Xi‘an University of Posts & Telecommunications. All rights reserved.
*/
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
#include <fstream>
#define INF 0xfffffff
using namespace std;
const int N = 5;
const int M = 10;
ifstream in;
enum status {UNSELECTED,SELECTED};
struct edge
{
int dest;
int weight;
};
struct vertex
{
int num;
int dist;
int inDegree,outDegree;
status _stat;
vertex * parent;
}V[N];
//The elements of priority queue
//The dest_vertex means the number of vertex, and dist means V[dest_vertex].dist
struct PQ_elem
{
int dest_vertex,dist;
};
//Overload the operator ‘<‘ so as to sort the priority queue
bool operator < (const PQ_elem &a, const PQ_elem &b)
{
return a.dist > b.dist;
}
vector<edge> AdjList[N];
vector<int> SELECTED_vertex;
priority_queue<PQ_elem> Edge_PQ;
void relax(int u, int v, int weight) //The "relax" operation
{
if(V[v].dist > V[u].dist + weight)
{
V[v].dist = V[u].dist + weight;
V[v].parent = &V[u];
}
}
void initialize(int s)
{
for(int i=0; i<N; i++)
{
V[i].num = i;
V[i].dist = INF;
V[i].parent = nullptr;
V[i].inDegree = 0;
V[i].outDegree = 0;
V[i]._stat = UNSELECTED;
AdjList[i].clear();
}
in.open("Dijkstra.txt");
for(int i=0; i<M; i++) //Read informations of edges and insert into the Adjacent List
{
int _start, _dest, _weight;
edge * tmp = new edge;
in>>_start>>_dest>>_weight;
tmp->dest = _dest;
tmp->weight = _weight;
V[_start].outDegree++;
V[_dest].inDegree++;
AdjList[_start].push_back(*tmp);
}
in.close();
V[s].dist = 0;
SELECTED_vertex.clear();
edge tmp_edge;
PQ_elem temp_PQ_elem;
//Push the vertices which adjacent to the source vertex into priority queue
for(int j=0; j<V[s].outDegree; j++)
{
tmp_edge = AdjList[s][j];
relax(s, tmp_edge.dest, tmp_edge.weight);
if(V[tmp_edge.dest]._stat == UNSELECTED)
{
temp_PQ_elem.dest_vertex = tmp_edge.dest;
temp_PQ_elem.dist = V[tmp_edge.dest].dist;
Edge_PQ.push(temp_PQ_elem);
}
}
}
//Print the shortest path from vertex s to v.
//If vertex s cannot reach vertex v, the function will print an error note on your display.
void print_path(vertex *s, vertex *v)
{
if(v == s)
cout<<s->num;
else if(v->parent == nullptr)
cout<<"No path from "<<s->num<<" to "<<v->num<<endl;
else
{
print_path(s,v->parent);
cout<<"->"<<v->num;
}
}
//The main function of Dijkstra algorithm
void Dijkstra(int s)
{
initialize(s);
//int numof_UNSELECTED = N-1;
SELECTED_vertex.push_back(s);
while(!Edge_PQ.empty())
{
PQ_elem temp_PQ_elem = Edge_PQ.top();
Edge_PQ.pop();
int this_vertex = temp_PQ_elem.dest_vertex;
edge tmp_edge;
for(int j=0; j<V[this_vertex].outDegree; j++)
{
tmp_edge = AdjList[this_vertex][j];
relax(this_vertex, tmp_edge.dest, tmp_edge.weight);
if(V[tmp_edge.dest]._stat == UNSELECTED)
{
temp_PQ_elem.dest_vertex = tmp_edge.dest;
temp_PQ_elem.dist = V[tmp_edge.dest].dist;
Edge_PQ.push(temp_PQ_elem);
}
}
V[this_vertex]._stat = SELECTED;
}
}
int main()
{
int s = 0;
Dijkstra(s);
cout<<"Succeed ! The distance of each vertex are :"<<endl;
for(int i=0; i<N; i++)
if(V[i].dist == INF)
cout<<"INF ";
else
cout<<V[i].dist<<" ";
cout<<endl<<"One of the shortest path is :"<<endl;
print_path(&V[0],&V[4]);
return 0;
}
/*
Pseudo Code :
Dijkstra(G,w,s)
S = empty set
Q = G.V - s
while Q != empty set
u = EXTRACT-MIN(Q)
S = S ∪ u
for each vertex v in AdjList[u]
relax(u,v,w)
*/
//Dijkstra.txt文件内容如下:
0 1 10
0 3 5
1 2 1
1 3 2
2 4 4
3 1 3
3 2 9
3 4 2
4 0 7
4 2 6
每一行的三个元素分别表示某条边的起始节点、终止节点、这条边的权重。
初学图论-Dijkstra单源最短路径算法基于优先级队列(Priority Queue)的实现
标签:
原文地址:http://my.oschina.net/bgbfbsdchenzheng/blog/489347