标签:
百度全体员工玩分组游戏,前面五分钟大家分头找队友,并将每个人找到的队友信息汇报给主持人,如果A和B是队友,B和C是队友,那么A和C也是队友;接着主持人不断地随机抽取两个人,希望判断二者是否为队友。请设计一个计算机程序辅助主持人判断两个人是否为队友,说明程序的关键算法,不需要代码实现。
例如:
<小明,小王>,<小军,小王>,<小丽,小李>是队友,那么小军和小明是队友,小军和小丽不是队友。
典型的并查集(Union-Find)应用。
并查集:我们可以把每个连通分量看成一个集合,该集合包含了连通分量的所有点。而具体的连通方式无关紧要,好比集合中的元素没有先后顺序之分,只有“属于”与“不属于”的区别。图的所有连通分量可以用若干个不相交集合来表示。而并查集的精妙之处在于用树来表示集合。
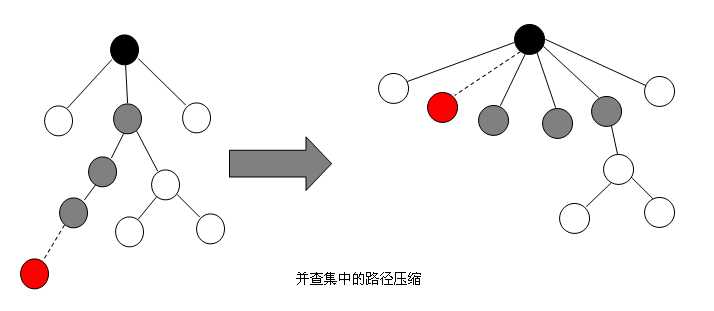
假设所有员工编号为1~n,那么一开始每个员工都属于自己的集合(假设为数组parents),采用的树结构则是每个员工结点的父结初始化为自己,即parents[i]=i;如果<i,j>为队友,那么将j的父结点设置为i,即parents[j]=parents[i],这样遍历所有的队友组合,就可以得到多棵树状的结构(每个集合为一棵树,见下图左);既然每个集合的元素都是队友,那么我们只需要将他们归为一类即可,因此需要将树进行压缩,压缩的过程就是不断的往上搜索(见下图右)。
如何判断两个员工是否为队友呢?只要看他们是否属于同一个集合,即同一个父结点。
并查集的应用:求最小生成树的Kruskal算法。
#include <iostream>
#include <vector>
using namespace std;
typedef pair<int,int> Pair;
void findParent(const vector<Pair> &friends,vector<int> &parents){
int sz=friends.size();
for(int i=0;i<sz;i++){
Pair cp=friends[i];
if(cp.first!=cp.second){
parents[cp.second]=parents[cp.first];
}
}
}
int getParent(const vector<int> &parents,int i){
while(i!=parents[i])
i=parents[i];
return i;
}
bool isFriend(const vector<int> &parents,Pair friends){
int f1=friends.first;
int f2=friends.second;
return getParent(parents,f1)==getParent(parents,f2);
}
int main()
{
vector<Pair> friends;
Pair p[5]={Pair(1,3),Pair(2,5),Pair(3,6),Pair(6,7),Pair(1,4)};
for(int i=0;i<5;i++){
friends.push_back(p[i]);
}
int num=7;
vector<int> parents(num+1);
for(int i=0;i<=num;i++)
parents[i]=i;
findParent(friends,parents);
Pair f(1,7);
cout<<isFriend(parents,f)<<endl;
return 0;
}
标签:
原文地址:http://www.cnblogs.com/AndyJee/p/4713154.html