标签:
这题做了好久,但是后面看来并不是想象中那么难。
例如一棵树
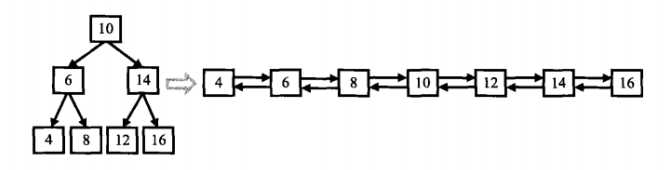
其实链表的顺序就是这棵树中根遍历的顺序,所以我想到了用递归或者非递归。
非递归的做法就是用栈对这棵树进行中根遍历,
用栈进行中根遍历的思路是,根节点的左子树先入栈,然后出栈,栈顶元素的右孩子入栈,直到栈空为止。
构建双链表时,记录前一个入栈的节点previous,当前出栈的节点current,然后把他们关联起来。
public static TreeNode Convert(TreeNode pRootOfTree) {
if(pRootOfTree==null){
return null;
}
if(pRootOfTree.left==null&&pRootOfTree.right==null){
return pRootOfTree;
}
//创建一个栈
LinkedList stack = new LinkedList();
TreeNode node =pRootOfTree;
//所有的左节点入栈
while(node!=null){
stack.push(node);
node=node.left;
}
TreeNode prehead=new TreeNode(0);
TreeNode previous=prehead;
//当栈不为空时
while(!stack.isEmpty()) {
//弹出栈顶元素
TreeNode current=(TreeNode) stack.pop();
//栈顶元素的右孩子入栈
if(current.right!=null) {
stack.push(current.right);
node=current.right.left;
while(node!=null){
stack.push(node);
node=node.left;
}
}
//将之前出栈的点和现在出栈的点建立联系
previous.right=current;
current.left=previous;
previous=current;
}
TreeNode newHead=prehead.right;
newHead.left=null;
return newHead;
}
递归做法我想了很久,因为总是想不到怎样把之前遍历过的记下来,剑指offer里面的好像也不对。
思路:
事实上根节点的left是指向左子树的最后一个节点,也就是最右边的节点,根节点的right是指向右子树最左边的节点。
根据这个规律,可以递归实现。
public static TreeNode convert(TreeNode pRootOfTree){
if(pRootOfTree==null) {
return null;
}
if(pRootOfTree.left==null&&pRootOfTree.right==null) {
return pRootOfTree;
}
//将左子树构造成双链表,并返回头节点
TreeNode left=convert(pRootOfTree.left);
TreeNode p=left;
//将左子树最后一个节点获取
while(p!=null&&p.right!=null) {
p=p.right;
}
if(p!=null) {
pRootOfTree.left=p;
p.right=pRootOfTree;
}
//将右子树构造成双链表,并返回头节点
TreeNode right=convert(pRootOfTree.right);
p=right;
//获取右子树的第一个节点
while(p!=null&&p.left!=null) {
p=p.left;
}
//若p不为空,关联pRootOfTree
if(p!=null) {
pRootOfTree.right=p;
p.left=pRootOfTree;
}
//判断left是否为空是为了避免没有左子树的情况
return left==null?pRootOfTree:left;
}
标签:
原文地址:http://www.cnblogs.com/qingfei1994/p/4917470.html