1099. Build A Binary Search Tree (30)

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

Both the left and right subtrees must also be binary search trees.

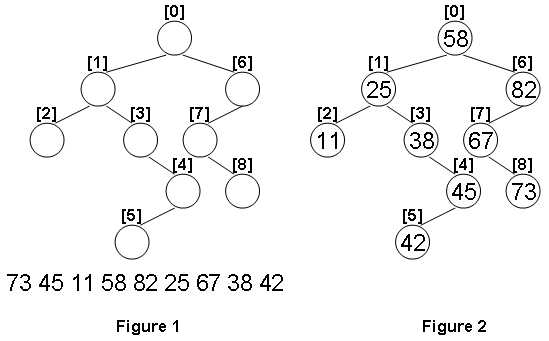
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (<=100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format "left_index right_index", provided that the nodes are numbered from 0 to N-1, and 0 is always the root. If one child is missing, then -1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

Output Specification:

For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output:

58 25 82 11 38 67 45 73 42

来源： <http://www.patest.cn/contests/pat-a-practise/1099>

 

#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
struct Node {
	int val;
	int left;
	int right;
};
Node node[101];
vector<Node*> nnn;
vector<int> num;
void Inorder(int i) {
	if (node[i].left != -1) {
		Inorder(node[i].left);
	//	nnn.push_back(node[node[i].left]);
	}
	Node *p = (Node*)malloc(sizeof(Node));
	p = &node[i];
	nnn.push_back(p);
	if (node[i].right != -1) {
		Inorder(node[i].right);
	//	nnn.push_back(node[node[i].right]);
	}
}
int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		int l, r;
		cin >> l >> r;
		node[i].left = l;
		node[i].right = r;
	}
	for (int i = 0; i < n; i++) {
		int temp;
		cin >> temp;
		num.push_back(temp);
	}
	sort(num.begin(), num.end());
	Inorder(0);
	for (int i = 0; i < n; i++) {
		//*nnn[i].val = num[i];
		nnn[i]->val = num[i];
	}
	queue<Node> q;
	q.push(node[0]);
	while (true)
	{
		if (q.front().left != -1) {
			q.push(node[q.front().left]);
		}
		if (q.front().right != -1) {
			q.push(node[q.front().right]);
		}
		
		cout << q.front().val;
		q.pop();
		if (q.empty())
			break;
		cout << " ";
	}
	return 0;
}

#include<iostream>
#include<queue>
#include<vector>
#include<algorithm>
#pragma warning(disable:4996)
using namespace std;
struct Node {
	int val;
	int left = -1;
	int right = -1;
};
vector<int> num;
Node node[101];
int n;
int cnt = 0;
void Inorder(int root) {
	if (node[root].left != -1)
		Inorder(node[root].left);
	node[root].val = num[cnt];
	cnt++;
	if (node[root].right != -1)
		Inorder(node[root].right);
}
int main(void) {
	freopen("Text.txt", "r", stdin);
	cin >> n;
	for (int i = 0; i < n; i++) {
		int l, r;
		cin >> l >> r;
		node[i].left = l;
		node[i].right = r;
	}
	for (int i = 0; i < n; i++) {
		int temp;
		cin >> temp;
		num.push_back(temp);
	}
	sort(num.begin(), num.end());
	Inorder(0);
	queue<Node> q;
	q.push(node[0]);
	while (true)
	{
		if (q.front().left != -1)
			q.push(node[q.front().left]);
		if (q.front().right != -1)
			q.push(node[q.front().right]);
		cout << q.front().val;
		q.pop();
		if (q.empty())
			break;
		cout << " ";
	}
	return 0;
}