标签:
from sklearn import decomposition import numpy as np A1_mean = [1, 1] A1_cov = [[2, .99], [1, 1]] A1 = np.random.multivariate_normal(A1_mean, A1_cov, 50) A2_mean = [5, 5] A2_cov = [[2, .99], [1, 1]] A2 = np.random.multivariate_normal(A2_mean, A2_cov, 50) A = np.vstack((A1, A2)) #A1:50*2;A2:50*2,水平连接 B_mean = [5, 0] B_cov = [[.5, -1], [-0.9, .5]] B = np.random.multivariate_normal(B_mean, B_cov, 100) import matplotlib.pyplot as plt plt.scatter(A[:,0],A[:,1],c=‘r‘,marker=‘o‘) plt.scatter(B[:,0],B[:,1],c=‘g‘,marker=‘*‘) plt.show() #很蠢的想法,把A和B合并,然后进行一维可分 kpca = decomposition.KernelPCA(kernel=‘cosine‘, n_components=1) AB = np.vstack((A, B)) AB_transformed = kpca.fit_transform(AB) plt.scatter(AB_transformed,AB_transformed,c=‘b‘,marker=‘*‘) plt.show() kpca = decomposition.KernelPCA(n_components=1) AB = np.vstack((A, B)) AB_transformed = kpca.fit_transform(AB) plt.scatter(AB_transformed,AB_transformed,c=‘b‘,marker=‘*‘) plt.show()
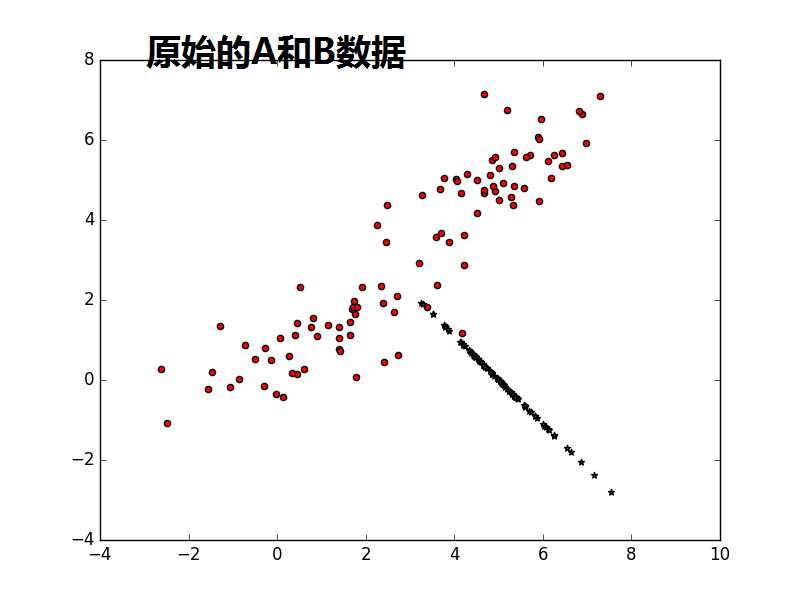
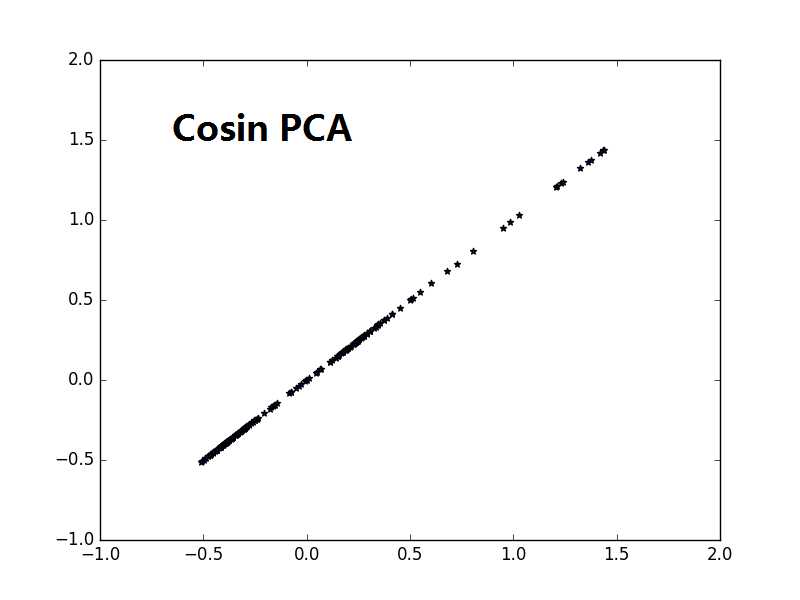
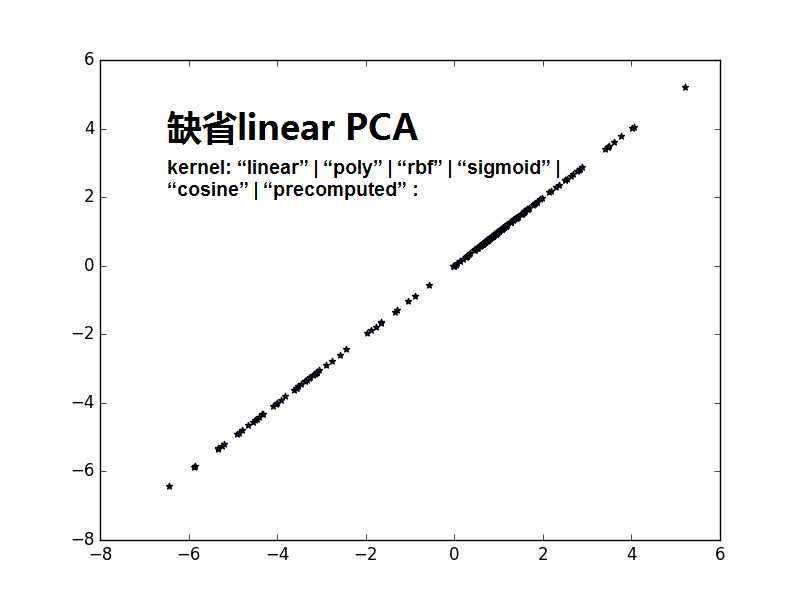
注意1:书上说consin PCA 比缺省的linear PCA要好,是不是consin PCA更紧致,数据不发散.
始终搞不懂什么时候用,什么时候不用
fit(X, y=None)
Fit the model from data in X.
ParametersX: array-like, shape (n_samples, n_features) :
Training vector, where n_samples in the number of samples and n_features is the numberof features.
fit_transform(X, y=None, **params)
Fit the model from data in X and transform X.
ParametersX: array-like, shape (n_samples, n_features) :
Training vector, where n_samples in the number of samples and n_features is the numberof features.
关于 sklearn.decomposition.KernelPCA的简单介绍
标签:
原文地址:http://www.cnblogs.com/qqhfeng/p/5294696.html