标签:
One-Shot Learning with a Hierarchical Nonparametric Bayesian Model
该篇文章通过分层贝叶斯模型学习利用单一训练样本来学习完成分类任务,模型通过影响一个类别的均值和方差,可以将已经学到的类别信息用到新的类别当中。模型能够发现如何组合一组类别,将其归属为一个有意义的父类。对一个对象进行分类需要知道在一个合适的特征空间中每一维度的均值和方差,这是一种基于相似性的度量方法,均值代表类别的基本标准,逆方差对应于类别相似性矩阵的各维度权重。One-Shot学习看起来似乎是不可能的,这是因为单一的样本只提供了相应类别的均值信息,而没有方差信息。如果给每个维度附以相同的权重或使用错误相似性矩阵,结果必定是不可靠的。
作者的模型利用从先前学习到的类别信息抽象出来的更高阶信息来估计新类别的基本标准以及适宜的相似性矩阵。随着所观测到的样本数的增多,这种估计的精度也随之提高。为了说明,考虑一下,当人类看到一个不熟悉动物时,如牛羚,很容易联想到马、牛、羊或是更为相似的物种。这是因为这些相似的物种有着更为相似的原型——马、牛、羊看起来相互长得更像,而并不像个什么家具或是汽车等。
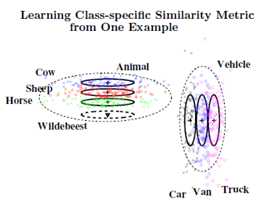
通过高维输入空间学习相似性矩阵已经成为机器学习领域一项重要任务。许多之前的工作主要针对于通过许多带标签的样本来学习相似性矩阵,没有试图去解决One-Shot学习问题。虽然启发于人类的学习过程,但本文方法也意指于广泛应用于机器分类和AI任务。从少量带标签样本学习并进行有效的推理任务是非常重要的。本文的方法是:无参数的先验可以使得在监督或无监督模式下的任何时候都能够生成新的类别。共轭分布集成大部分参数并能够进行快速推理。
1. 分层贝叶斯模型
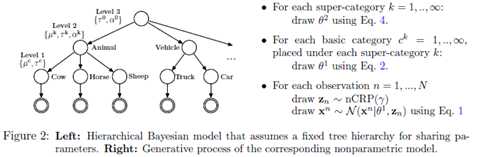
考虑观测一个有$N $个独立同分布的输入特征向量$\{x^1,...,x^N\} $,$x^n\in R^D $,$D $是特征的维度。假定这$N $个对象被分配到$C $个基类(level-1),我们通过一个长度为$N $的向量$z^b $来表示这种分配关系,即$z_{n}^b\in \{1,...,C\} $。同样,我们也假设这个$C $基类属于$K $个超类(level-2)当中,我们用一个长度为$C $的向量$z^s $来表示这种关系,$z_{c}^s\in \{1,...,K\} $。
对于任一基类$c $,假设其观测到的特征向量服从高斯分布$N(x|\mu,1/\tau) $,则有
$$
P(x^n|z_{n}^b=c,\theta^1)=\prod_{d=1}^D N(x_{d}^n|\mu_{d}^c,1/\tau_{d}^c)
$$
其中$\theta^1=\{\mu^c,\tau^c\}_{c=1}^C $表示level-1的类别参数。
然后我们假定$\{\mu^c,\tau^c\} $服从共轭的正态—伽马分布。level-1的c类属于level-2的k类可以表示为$k=z_{c}^s $,用$\theta^2=\{\mu^k,\tau^k,\alpha^k\}_{k=1}^K $表示level-2的参数。那么$P(\mu^{c},\tau^c|\theta^2,z^s)=\prod_{d=1}^D P(\mu_{d}^c,\tau_{d}^c|\theta^2,z^s) $
对于每个维度$d$
$$
P(\mu_{d}^c,\tau_{d}^c|\theta^2)=P(\mu_{d}^c|\tau_{d}^c,\theta^2)P(\tau_{d}^c,\theta^2)=N(\mu_{d}^c|\mu_{d}^k,1/(\nu \tau_{d}^c)\Gamma (\tau_{d}^c|\alpha_{d}^k,\alpha_{d}^k/\tau_{d}^k))
$$
其中
$$
\Gamma(\tau|\alpha^k,\alpha^k/\tau^k)=\frac{(\alpha^k/\tau^k)^{\alpha^k}}{\Gamma(\alpha^k)}\tau^{\alpha^k-1} \exp \Big(-\tau\frac{\alpha^k}{\tau^k}\Big)
$$
这样的初始化能够给我们的模型以直观的解释,因为$E[\mu^c]=\mu^k $且$E[\tau^c]=\tau^k $,因此level-2的参数$\theta^2 $正好对应于level-1参数$\theta^1 $的期望,参数$\alpha^k $进一步控制着$\tau^c $围绕均值的变化。对于level-2层参数$\theta^2 $,我们假设下列的共轭先验:
\[
P(\mu_{d}^k)=N(\mu_d^k|0,1/\tau^0),\;P(\alpha_d^k|\alpha^0)=Exp(\alpha_d^k|\alpha^0),\;P(\tau_d^k|\theta^0)=IG(\tau_d^k|\alpha^0,b^0)
\]
$Exp(x|\alpha) $是参数为$\alpha $的指数分布,$IG(x|\alpha,\beta) $是参数为$\alpha $和$\beta $的逆伽马分布。我们进一步假设level-3参数$\theta^3=\{\alpha^0,\tau^0\} $服从弥散伽马分布$\Gamma(1,1) $
2. Chinese Restaurant Process
至此,我们已经假设我们的模型分为两层$z=\{z^s,z^b\} $,然而,如果我们没有获得任何的level-1和level-2的类标签,我们就需要推断可能的类结构分布。我们假定服从无参数的两层嵌套Chinese-Restaurant Prior(CPR)分布。Chinese Restaurant Process是定义在整数部分的一种分布。想象一下这个过程,当顾客进入一个没有桌子数量限制的饭店,那么第$n$个顾客坐在桌子$k$的概率可以用下列分布来刻画:
$$
P(z_n=k|z_1,...,z_{n-1})=
\begin{cases}
\frac{n^k}{n-1+\gamma} & n^k>0 \\
\frac{\gamma}{n-1+\gamma} &k\;is\;new
\end{cases}
$$
$n^k $是桌子$k$之前所有的顾客数,$\gamma $是集中参数。
嵌套CRP,即$nCRP(\gamma) $是将$CRP $扩展成树每层划分的嵌套序列,在这种情况下,每个观测值$n $首先通过上述方程分配到父类$z_n^s $,然后再一次按照上述方程将其分配到父类$z_n^s $下的基类$z_b^s $。最后假定$\gamma \sim \Gamma(1,1) $。不像传统的分层贝叶斯模型,本文的模型参数和分层参数都是共享的。
3. 推理
模型参数在各个层上的推理都是采用$MCMC $的方法。当模型的树结构没有给定时,推理中首先固定,然后采样模型参数$\theta $,固定$\theta $去采样类别分配,两个过程交替进行。
采样level-1和level-2参数:
给定level-2参数$\theta^2 $和$z $,条件分布$P(\mu^c,\tau^c|\theta^2,z,x) $是$Normal-Gamma $分布,这使得我们很容易去采样level-1的参数$\{\mu^c,\tau^c\} $。给定$z,\;\theta^1,\;\theta^3 $后,$\mu^k,\;\tau^k $服从高斯和逆伽马分布,同样很容易采样就得。唯一复杂一点的是采样$\alpha^k $,因为
$$
p(\alpha^k|z,\theta^1,\theta^3,\tau^k)\propto \frac{(\alpha^k/\tau^k)^{\alpha^k n_k}}{\Gamma(\alpha^k)^{n_k}}\exp\Big(-\alpha^k\Big(\alpha^0+S^k/\tau^k-T^k\Big)\Big)
$$
其中$S^k=\sum_{c:z(c)=k}\tau^c $且$T^k=\sum_{c:z(c)=k}\log(\tau^c) $,若$\alpha^k $较大,上述概率密度近似于伽马密度,因此,我们可以用$Metropolis-Hastings $方法。我们生成一个新的候选变量
$$
\alpha^*\sim Q(\alpha^*|\alpha^k)\;with\;Q(\alpha^*|\alpha^k)=\Gamma(\alpha^*|t,t/\alpha^k)
$$
然后用$M-H $方法进行采样。
采样$z $:
给定模型参数$\theta=\{\theta^1,\theta^2\} $后,$z_n $的后验分布为:
$$
p(z_n|\theta,z_{-n},x^n)\propto p(x^n|\theta,z_n)p(z_n|z_{-n})
$$
其中$z_{-n} $是指$z$中除了$n$以后的所有观测值。
当计算所创建出的新基类的概率时,我们能够进一步利用分层模型的共轭性。由于服从正态—伽马先验的$p(\mu^c,\tau^c) $是一个正态分布的共轭先验,因此,我们能够很容易计算下列边缘似然概率:
$$
p(x^n|\theta^2,z_n)=\int_{\mu^c,\tau^c}p(x^n,\mu^c,\tau^c|\theta^2,z_n)=\int_{\mu^c,\tau^c}p(x^n|\mu^c,\tau^c)p(\mu^c,\tau^c|\theta^2,z_n)
$$
积掉基类参数$\theta^1 $能够让我们更有效地从树结构中进行采样。当计算新父类下$x^n $的概率时,它的参数可以从先验分布中采样获得。
4. One-Shot Learning
考虑观察到一个新类$c^* $的新样本$x^* $,在level-2参数$\theta^2 $当前设置以及当前树结构确定的情况下,我们能够首先推断出这个新类是属于哪个父类,例如我们能够计算$z_c^* $的后验分布。如果没有相匹配的父类,就创建自己的父类。当给定一个推断出的$z_c^* $时,我们就能够求得新类的均值和相似性矩阵$\{\mu^*,\tau^*\} $。我们可以通过计算新的测试输入$x^t $属于新类$c^* $的条件概率来测试HB模型的泛化性能。
$$
p(c^*|x^t)=\frac{p(x^t|z_c^*)p(z_c^*)}{\sum_z p(x^t|z)p(z)}
$$
这里,先验概率可以由$nCRP(\gamma) $来确定,log似然形式如下:
$$
\log p(x^t|c^*)=\frac{1}{2}\sum_d \log(\tau_d^*)-\frac{1}{2}\sum_d \tau_d^*(x_d^t-\mu_d^*)^2+C
$$
$C $是一个常数,不依赖于任何参数。
5. MNIST实验
本文首先研究了HB模型泛化单个样本——手写体9的能力。首先采用900幅图片(0-8每个数字100幅)来训练HB模型,然后给定一个数字9,模型能够发现新的类别与4和7所在的类别很相近,因此新类能够通过4和7所在类别的均值和相似矩阵来计算自己的参数。
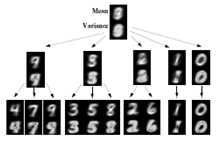
参考文献:
Salakhutdinov, Ruslan, Joshua B. Tenenbaum, and Antonio Torralba. "One-Shot Learning with a Hierarchical Nonparametric Bayesian Model." ICML Unsupervised and Transfer Learning. 2012.
标签:
原文地址:http://www.cnblogs.com/huangxiao2015/p/5668140.html