标签:


题意:
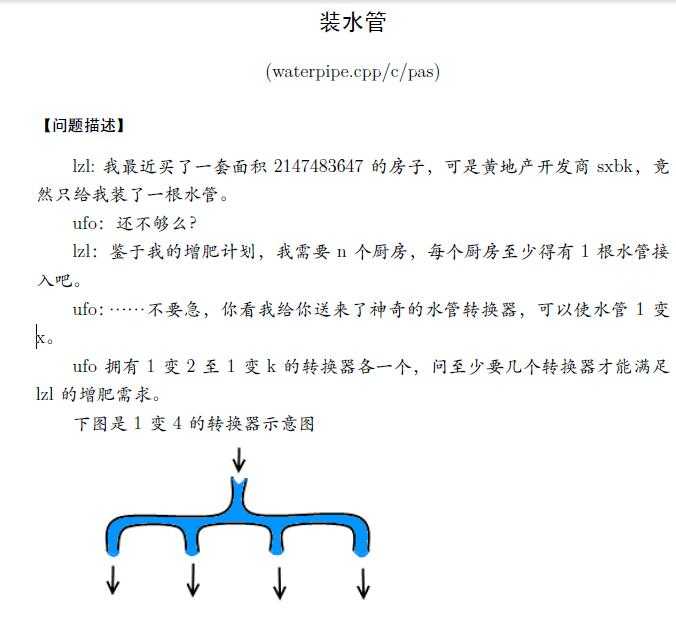
各有一变2,一变3,...一变k(2<=k<=109)的水管1根,求用最少的水管使得1变n(1<=n<=1018)。
题解:
0.采用贪心的策略,应该先用1变多的水管。
1.第一次接一变K的水管,那么之后接的水管应该为1变k-1号的,增加的出水口是k-2,以此类推那么可以列出用完所有管子的式子k+(k-2)+(k-3)+(k-4)+...1,那么就可以采用等差数列的公式进行计算。
2.进行计算有两种方式:第一种二分,第二种用不等式求解。
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL unsigned long long
LL n,k;
bool check(LL x){
LL ret = k;
ret += (2*k-2-x)*(x-1)>>1;
if(ret >= n)return true;
else return false;
}
int main(){
freopen("waterpipe.in","r",stdin);
freopen("waterpipe.out","w",stdout);
cin>>n>>k;
LL l = 0,r = k;
LL tot = (k-1)*(k-2)/2+k;
if(tot<n){cout<<"-1"<<endl;return 0;}
if(n <= k){cout<<"1"<<endl;return 0;}
if(n == 1){cout<<"0"<<endl;return 0;}
while(l < r){
int mid = l+r>>1;
if(check(mid))r = mid;
else l = mid+1;
}
cout<<l<<endl;
return 0;
}


题意:
给出一个长度为n(<=1000000)字符串,求在区间里面某个出现次数最多的字符与次数最少的字符差的最大值。
题解:
0.最暴力的方式是两层循环,枚举当前位置i,再枚举之前的位置j(0<=j<i),如果cnt[pos][alp]表示在1~pos这个区间字符alp出现的次数,那么答案就是
max{(cnt[i][ch0]-cnt[j][ch0])-(cnt[i][ch1]-cnt[j][ch1])}(ch0和ch1(‘a‘~‘z‘))
1.变形后就是max{(cnt[i][ch0]-cnt[i][ch1])-(cnt[j][ch0]-cnt[j][ch1])}那么只需要维护(cnt[j][ch0]-cnt[j][ch1])的极小值。复杂度为O(26*n)
代码:
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int n,ret,mini[30][30],cnt[30];
char str[N];
int main(){
freopen("string.in","r",stdin);
freopen("string.out","w",stdout);
scanf("%d%s",&n,str);
memset(mini,127,sizeof(mini));
for(int i = 0;i < n;++i){
int ch = str[i]-‘a‘;
++cnt[ch];
for(int j = 0;j < 26;++j){
if(ch == j || !cnt[j])continue;
ret = max(ret,cnt[ch]-cnt[j]-mini[ch][j]);
mini[ch][j] = min(mini[ch][j],cnt[ch]-cnt[j]);
mini[j][ch] = min(mini[j][ch],cnt[j]-cnt[ch]);
}
}
cout<<ret<<endl;
return 0;
}



题意:
在有n(<=5*106)个节点的树上,给出k(<=5*106)朵花,给出距离d(<=5*106),求有多少个点满足从自身出发d的距离能够覆盖所有的花?
题解:
0.如果以这个点为圆心,半径为d,画圆能够覆盖所有的花,那么这个点就满足条件。
1.那么就只需要找到所有的花组成的生成树的最远点和次远点,最远点和次远点连线就是生成树的直径,如果某个点满足距离 最远点和次元点都不超过d,那么这个点就是满足条件的。
代码:
#include <cstdio>
#include <queue>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5000010;
struct edge{int v;edge *nxt;}meo[N<<1],*head[N],*c;
bool vis[N];
int ncnt = 1,n,k,d,u,v,f[N],dis0[N],x,dis1[N],ret;
int readint(){
char c;int sign = 1,k = 0;c = getchar();
while(c > ‘9‘ || c < ‘0‘){if(c == ‘-‘)sign = -1;c = getchar();}
while(c <= ‘9‘ && c >= ‘0‘){k = k*10+c-‘0‘;c = getchar();}
return k*sign;
}
void addedge(int u,int v){
c->v = v,c->nxt = head[u],head[u] = c++;
}
void bfs(int s,int *dis){
queue <int> q;
memset(vis,0,sizeof(vis));
q.push(s),vis[s] = 1,dis[s] = 0;
while(!q.empty()){
int u = q.front();q.pop();
for(edge *it = head[u];it;it = it->nxt){
int v = it->v;
if(!vis[v]){q.push(v),vis[v] = 1,dis[v] = dis[u]+1;}
}
}
}
int main(){
freopen("blossom.in","r",stdin);
freopen("blossom.out","w",stdout);
c = meo;
n = readint(),k = readint(),d = readint();
for(int i = 1;i <= k;++i)f[i] = readint();
for(int i = 1;i < n;++i){
u = readint(),v = readint();
addedge(u,v);addedge(v,u);
}
bfs(x = f[1],dis0);
for(int i = 1;i <= k;++i)x = dis0[x]<dis0[f[i]] ? f[i] : x;
bfs(x,dis0);
for(int i = 1;i <= k;++i)x = dis0[x]<dis0[f[i]] ? f[i] : x;
bfs(x,dis1);
for(int i = 1;i <= n;++i)if(dis0[i]<=d && dis1[i]<=d)ret++;
cout<<ret<<endl;
return 0;
}
标签:
原文地址:http://www.cnblogs.com/xgtao984/p/5770554.html