标签:
最近突然有兴致hiho一下了,实现了下trie tree,感觉而言,还是挺有意思的,个人觉得这货不光可以用来查单词吧,其实也可以用来替代Hash,反正查找,插入复杂度都挺低的,哈哈,啥都不懂,瞎扯....废话不多,正题开始!
题目截下:
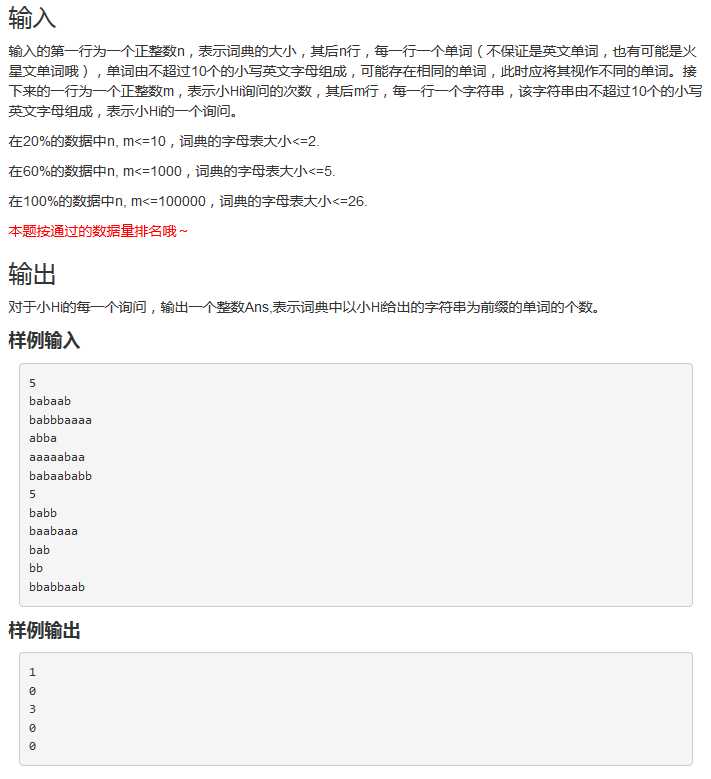
Trie Tree用来干啥呢,套用Hiho上的解释,比如存在一个字典,里面存在10000个单词,需要查找以xxx为前缀的单词个数,按照常规思维,10000 个单词,挨个比对,哇,复杂度爆炸!所以此时呀,将这些单词以树的形式存储,每个节点存放一个字符,这样一来,添加一个词组,只需从根节点从上之下添加, 并将经过的节点计数加1,这样便可以统计拥有同一前缀的单词个数了,哎,不得不说,这种用树结构来存储词组的方法还真是方便,无论查找或者添加。说了这么 多,开始上代码,对了,写代码这次采用的从上之下的方式,不得不说,也是有种不同的感受.....
按照题目要求,可有以下代码:
int main()
{
TrieTree tt;
int a = 0;
cin >> a;
string s = "";
char t[20];
for (int i = 0; i < a; i++)
{
cin >> t;
s = t;
tt.add(t);
}
cin >> a;
for (int i = 0; i < a; i++)
{
cin >> t;
s = t;
cout<<tt.search(t)<<endl;
}
return 0;
}
由题中要求,显然TrieTree需要实现add,search操作
class TrieTree
{
public:
TrieTree();
void add(string s);
int search(string s);
private:
TrieNode root;
};
TrieTree::TrieTree():root(0)
{
}
void TrieTree::add(string s)
{
TrieNode *t = &root;
for (int i=0;i<s.length();i++)
{
t=t->add(s[i]);
}
}
int TrieTree::search(string s)
{
TrieNode *t = &root;
int num = 0;
for (int i = 0; i < s.length(); i++)
{
t=t->search(s[i]);
if (t == NULL)
return 0;
}
return t->num;
}
继续实现TrieNode:
class TrieNode
{
public:
char c;
int num;
list<TrieNode*> tnv;
TrieNode* add(char c);
TrieNode* search(char c);
TrieNode(char c);
};
TrieNode::TrieNode(char c)
{
this->c = c;
num = 0;
}
TrieNode *TrieNode::add(char c)
{
auto t = tnv.begin();
while (t!=tnv.end())
{
if ((*t)->c == c)
{
(*t)->num++;
return *t;
}
t++;
}
TrieNode *m = new TrieNode(c);
m->num++;
tnv.push_back(m);
return m;
}
TrieNode *TrieNode::search(char c)
{
auto t = tnv.begin();
while (t != tnv.end())
{
if ((*t)->c == c)
{
return *t;
}
t++;
}
return NULL;
}
标签:
原文地址:http://www.cnblogs.com/Rainlee007/p/5784948.html