标签:优先 index stl 先后 roc 节点 back ons lib

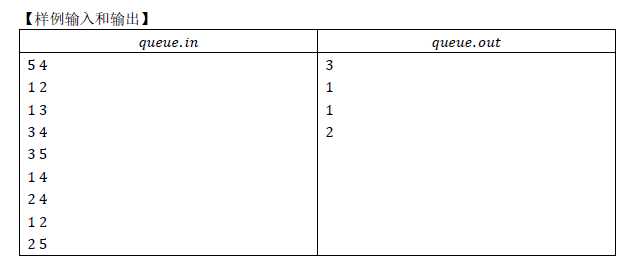
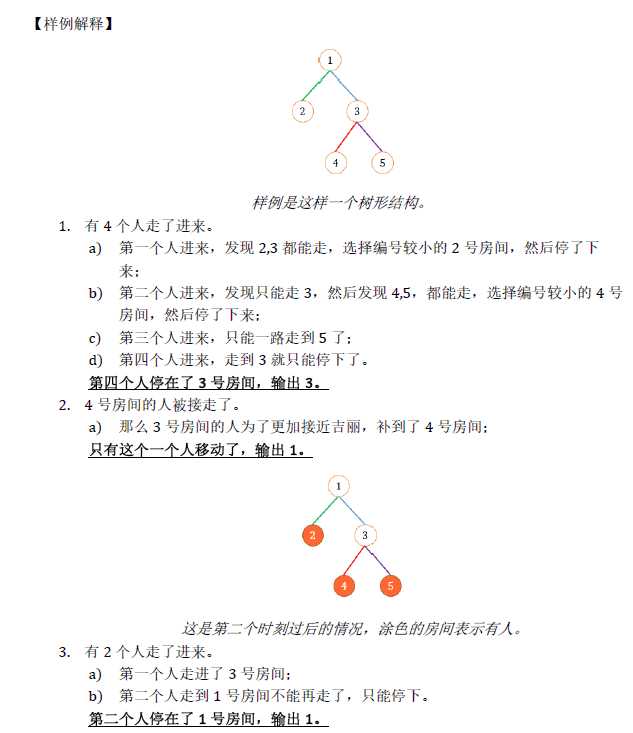

就是这样一道题了。
维护这一棵树。
对于第一种操作,我们从题意可知,节点的访问顺序就是DFS序,至于先小后大的限制,只需要用伟大的STL-sort来逐层排序就很好了,代码简洁,时间复杂度低。
按DFS序把这些点存入优先队列,如果该点没人,就在该队列中,人的流动先后顺序就可以用出入优先队列来维护。
对于第二种操作。这里用到了倍增的思想寻找第一个有人的祖宗点,那么这个点下次就要优先进人,所以进队。
#include<cstdio>#include<cstdlib>#include<cstring>#include<algorithm>#include<vector>#include<queue>using namespace std;vector<int>sa[100005];int dad[100005][28],p[100005],id=0;int n,t;void dfs(int x,int fa){ dad[x][0]=fa; int nn=sa[x].size(); for (int i=0;i<nn;i++) { if (sa[x][i]!=fa) { dfs(sa[x][i],x); } } p[x]=++id;}int tf[100005];struct node{ int x; node(){}; node(int x):x(x){}; bool operator<(const node&a) const {return p[x]>p[a.x];}};priority_queue<node>sb;int find(int x,int &ans){ for (int i=20;x!=1&&i>=0;i--) { if (dad[x][i]>0&&tf[dad[x][i]]==false) { x=dad[x][i];ans+=(1<<i); } } return x;}int main(){ scanf("%d%d",&n,&t); for (int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); sa[x].push_back(y); sa[y].push_back(x); } for (int i=1;i<=n;i++) sort(sa[i].begin(),sa[i].end()); dfs(1,0); for (int i=1;i<=20;i++) for (int j=1;j<=n;j++) { dad[j][i]=dad[dad[j][i-1]][i-1]; } for (int i=1;i<=n;i++) sb.push(node(i)),tf[i]=true; for (int i=1;i<=t;i++) { int op,x,ans=0; scanf("%d%d",&op,&x); if (op==1) { node soy; while(x--) { soy=sb.top(); sb.pop(); tf[soy.x]=false; } ans=soy.x; } else { int soy=find(x,ans); sb.push(node(soy));tf[soy]=true; } printf("%d\n",ans); }}标签:优先 index stl 先后 roc 节点 back ons lib
原文地址:http://www.cnblogs.com/Notok/p/6042635.html