标签:com 角度 highlight 相关度 9.png font 偏差 数列 sign
P1问题求解相关算法
1. BP
利用matlab的线性规划工具箱,即linprog
主要思想:如何将P1问题转换为线性规划问题
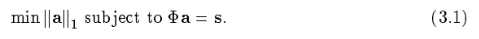
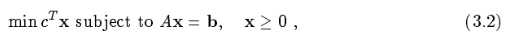
即由3.1变为3.2
令x=[u; v],其中u,v均为正,a=u-v
A=[phi,-phi] (显示不了符号,读出来就好。。。 )
b=s
则b=Ax=(u-v)=a=s
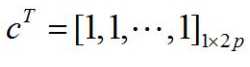
求解:x0=linprog(c,[],[],A,b,zeros(2*p,1));
问题P1的最优解即为x0(1:p)-x0(p+1:2p)
注:这里要去掉绝对值,证明如下:


2. BPDN 基追踪去噪
利用quadprog
x0=quadprog(B,c,[],[],[],[],zeros(2*m,1));
x0=x0(1:m)-x0(m+1:2*m);
和BP思想一样,将P1问题转换为二次规划问题,
令x=u-v
不一样的地方是,BPDN允许噪声的存在,可以参考IRLS-noNoise和IRLS的区别。
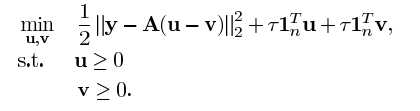
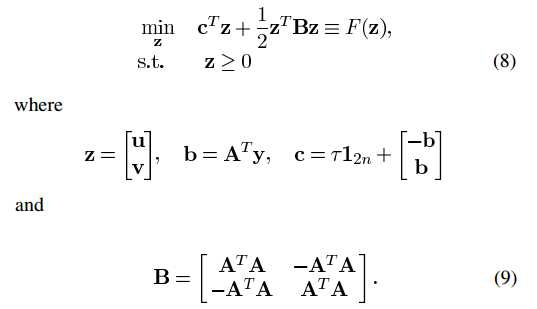
n=20;m=30;
A=randn(n,m);
W=sqrt(diag(A‘*A));
for k=1:1:m
A(:,k)=A(:,k)/W(k);
end
S=5;
x=zeros(m,1);
pos=randperm(m);
x(pos(1:S))=sign(randn(S,1)).*(1+rand(S,1)); %x的稀疏度为S,即稀疏度逐渐增加到Smax
b=A*x;
lamda=0.0001*2.^(0:0.75:15);
for i=1:1:21
%{
%BP
bb=A‘*b;
c=lamda(i)*ones(2*m,1)+[-bb;bb];
B=[A‘*A, -A‘*A;-A‘*A, A‘*A];
x0=quadprog(B,c,[],[],[],[],zeros(2*m,1));
x0=x0(1:m)-x0(m+1:2*m);
%}
%BPDN
bb=A‘*b;
c=lamda(i)*ones(2*m,1)+[-bb;bb];%注意lamda取值,这里取为0.05
B=[A‘*A, -A‘*A;-A‘*A, A‘*A];
x0=quadprog(B,c,[],[],[],[],zeros(2*m,1));
x0=x0(1:m)-x0(m+1:2*m);
err(i)=(x0-x)‘*(x0-x)/(x‘*x);
end
h=semilogx(lambda,err,‘k--‘);
set(h,‘LineWidth‘,2);
3.IRLS 迭代重加权最小二乘
将l0松弛到l1,得到P1,即BPDN(基追踪降噪 basis pursuit denoising),将P1写成标准的优化问题即Q1,添加拉格朗日乘子。
一般定义Q1为套锁回归(LASSO)
主要思想:为方便对问题Q1求导,
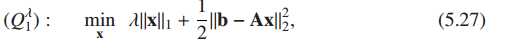
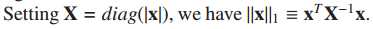
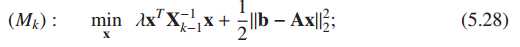
输入A、x、b、
问题M的最小二乘求解:
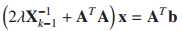
xout=inv(2*lambda(ll)*XX+AA)*Ab;
对角加权矩阵X的更新,XX为X的逆:
XX=diag(1./(abs(xout)+1e-10));
当||小于预设阈值时停止迭代
输出问题Q1的近似解
n=100; m=200; S=4; sigma=0.1;
A=randn(n,m);
W=sqrt(diag(A‘*A));
for k=1:1:m,
A(:,k)=A(:,k)/W(k);
end;
x0=zeros(m,1);
pos=randperm(m);
x0(pos(1:S))=sign(randn(S,1)).*(1+rand(S,1));
b=A*x0+randn(n,1)*sigma;
% The IRLS algorithm for varying lambda
Xsol=zeros(m,101);
Err=zeros(101,1);
Res=zeros(101,1);
lambda=0.0001*2.^(0:0.15:15);
AA=A‘*A;
Ab=A‘*b;
for ll=1:1:101
xout=zeros(m,1);
XX=eye(m);%单位对角矩阵
for k=1:1:15
xout=inv(2*lambda(ll)*XX+AA)*Ab;
XX=diag(1./(abs(xout)+1e-10));
% disp(norm(xout-x0)/norm(x0));
end;
Xsol(:,ll)=xout;
Err(ll)=(xout-x0)‘*(xout-x0)/(x0‘*x0);%误差
Res(ll)=(A*xout-b)‘*(A*xout-b)/sigma^2/n; %残差
end;
如何选择拉格朗日乘子?
经验法则:选择接近噪声偏差值和期望非零值的标准差的比值
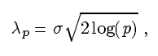
注:残差和噪声功率相等时取得最优
确定最优方法:根据经验法则确定大致值lambda=0.0001*2.^(0:0.15:15);
对进行验算,最小误差对应的即最优
posL=find(Err==min(Err),1);
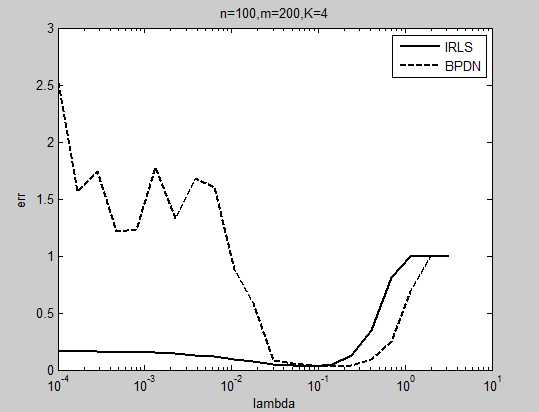
注:BPDN执行较IRLS慢
4. LARS(least angle regression stagewise)最小角度回归分布
这个要多写点~
forward selection 和OMP的思想比较接近
forward stagewise感觉就是更加平滑,因为步长更小
LAR取的步长是两者之间,即最小角度回归。
结合两者的思想即为LARS。
主要思想:
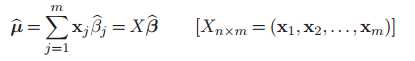
为稀疏(回归)系数列向量,为估计向量
首先取,即
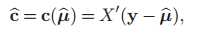
c正比于X和当前残差向量的相关度(怪怪的。。)
取|cj|最大的方向
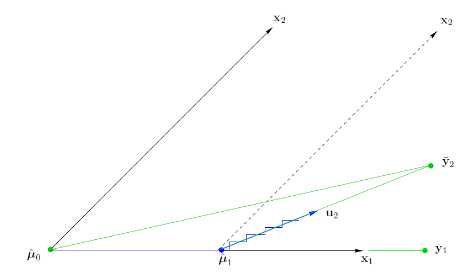

算法步骤:
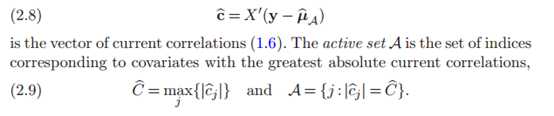
为方便理解,可引入XA
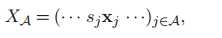
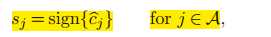
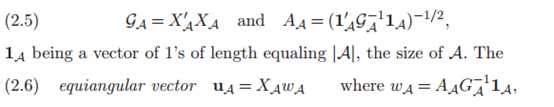

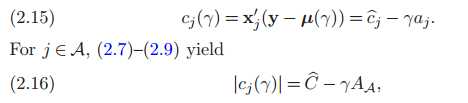
联立15.16两式:
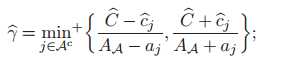
3.更新mu

4.求bita
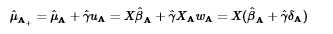
n=100; m=200; S=4; sigma=0.1;
A=randn(n,m);
W=sqrt(diag(A‘*A));
for k=1:1:m,
A(:,k)=A(:,k)/W(k);
end;
x0=zeros(m,1);
pos=randperm(m);
x0(pos(1:S))=sign(randn(S,1)).*(1+rand(S,1));
b=A*x0+randn(n,1)*sigma;
Err=zeros(n,1);
Res=zeros(n,1);
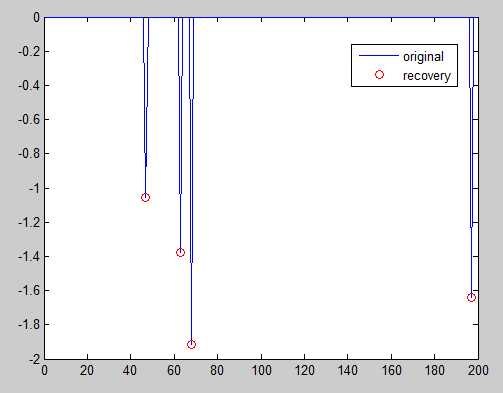
XsolLARS=lars(A,b);%求稀疏向量
for k=1:1:n
xout=XsolLARS(k,:)‘;
ErrLARS(k)=(xout-x0)‘*(xout-x0)/(x0‘*x0);
end;
function beta = lars( X,y )
%求稀疏向量
[n,m]=size(X);
nvars=min(n-1,m);%%???
mu=zeros(n,1);
beta = zeros(2*nvars, m);
I=1:m;
A=[];k=0;vars=0;
gram=X‘*X;
while vars<nvars
k=k+1;
c=X‘*(y-mu);
[C,j]=max(abs(c(I)));%c(I) 即不包含之前取过的j
j=I(j);
A=[A j];
vars=vars+1;
I(I==j)=[];%这里不是置零,而是直接去掉j
s=sign(c(A));
G=s‘*inv(gram(A,A))*s;
AA=G^(-1/2);
WA=AA*inv(gram(A,A))*s;
u=X(:,A)*WA;
if vars==nvars
gamma=C/AA;
else
a=X‘*u;
temp=[(C-c(I))./(AA-a(I));(C+c(I))./(AA+a(I))];%减去c、a中不属于A的j列向量,从而得到gamma
gamma=min([temp(temp>0);C/AA]);
end
mu=mu+gamma*u;
beta(k+1,A) = beta(k,A) + gamma*WA‘;
end
if size(beta,1) > k+1
beta(k+2:end, :) = [];%只取nvars个,beta即为稀疏向量
end
end
拓展:硬阈值、软阈值
如果A 是酋矩阵,则AA(t)=I,故P0问题可写为:
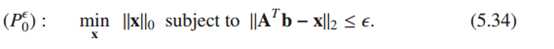
令
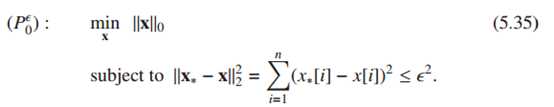
误差最小的解,即为接近的最稀疏向量,只需将的各项按绝对值降序排列选择前几项即可。
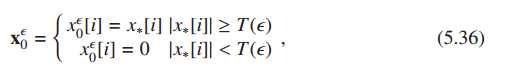
其中T()为硬阈值。怎么取?
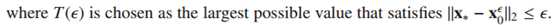
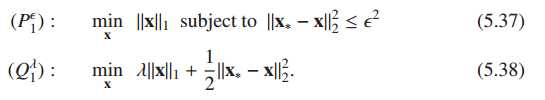
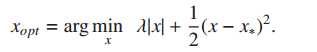
用LARS的思想
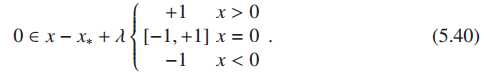
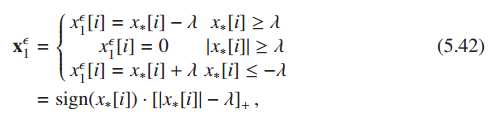
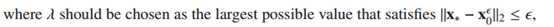 lambda即为软阈值
lambda即为软阈值
标签:com 角度 highlight 相关度 9.png font 偏差 数列 sign
原文地址:http://www.cnblogs.com/fanmu/p/6061223.html