标签:des style blog http color os io strong
http://poj.org/problem?id=3744
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 4850 | Accepted: 1288 |
Description
Input
Output
Sample Input
1 0.5 2 2 0.5 2 4
Sample Output
0.5000000 0.2500000
http://www.cnblogs.com/yan-boy/archive/2012/11/29/2795294.html
显然,如果k 号位有雷,那么安全通过这个雷只可能是在 k-1 号位选择走两步到 k+1 号位。因此,可以得到如下结论:在第 i 个雷的被处理掉的概率就是从 a[i-1]+1 号位到 a[i] 号位的概率。于是,可以用 1 减去就可以求出安全通过第 i 个雷的概率,最后乘起来即可,比较悲剧的是数据很大,所以需要用到矩阵快速幂……
类似斐波那契数列,有ans[i]=p*ans[i-1]+(1-p)*ans[i-2] ,构造矩阵为
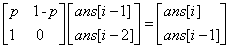

#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> using namespace std; int x[40]; double p; struct matrix { double a[2][2]; }; bool cmp(int x,int y) { return x<y; } matrix multiply(matrix x,matrix y) { matrix temp; memset(temp.a,0,sizeof(temp.a)); for(int i=0;i<2;i++) { for(int j=0;j<2;j++) { for(int k=0;k<2;k++) { temp.a[i][j]+=x.a[i][k]*y.a[k][j]; } } } return temp; } matrix calc(matrix origin,int n) { matrix res; memset(res.a,0,sizeof(res.a)); res.a[0][0]=res.a[1][1]=1; while(n) { if(n&1) res=multiply(res,origin); origin=multiply(origin,origin); n>>=1; } return res; } int main() { int n,i,j; double ans; while(~scanf("%d%lf",&n,&p)) { memset(x,0,sizeof(x)); ans=1; for(i=0;i<n;i++) scanf("%d",&x[i]); sort(x,x+n,cmp); matrix origin,ff; origin.a[0][0]=p; origin.a[0][1]=1-p; origin.a[1][0]=1; origin.a[1][1]=0; ff=calc(origin,x[0]-1); ans*=(1-ff.a[0][0]); for(i=1;i<n;i++) { if(x[i]==x[i-1]) continue; ff=calc(origin,x[i]-x[i-1]-1); ans*=(1-ff.a[0][0]); } printf("%.7lf\n",ans); } return 0; }
poj 3744 Scout YYF I,布布扣,bubuko.com
标签:des style blog http color os io strong
原文地址:http://www.cnblogs.com/cancangood/p/3916484.html