标签:png under cli turn lambda 最小值 abs tor amp
首先拿出最后要求解的问题:$\underset{\alpha}{min}W(\alpha)=\frac{1}{2} \sum_{i,j=1}^{n}y^{(i)}y^{(j)}\alpha_{i}\alpha_{j}k_{ij}-\sum_{i=1}^{n}\alpha_{i}$,使得满足:
(1)$0 \leq \alpha_{i}\leq C,1 \leq i \leq n$
(2)$\sum_{i=1}^{n}\alpha_{i}y^{(i)}=0$
求解的策略是每次选出两个$\alpha$进行更新。比如选取的是$\alpha_{1},\alpha_{2}$。由于$\sum_{i=1}^{n}\alpha_{i}y^{(i)}=0$,所以$\alpha_{1}y^{(1)}+\alpha_{2}y^{(2)}=-\sum_{i=3}^{n}\alpha_{i}y^{(i)}$。等号右侧是一个常数,设为$\xi$。当$y^{(1)}$和$y^{(2)}$异号时,有$\alpha_{1}-\alpha_{2}=\xi$或者$\alpha_{2}-\alpha_{1}=\xi$。同时它们还要满足$0\leq \alpha \leq C$。
我们设$\alpha_{2}$的合法区间为[L,R],那么此时有$L=max(0,\alpha_{2}-\alpha_{1}),R=min(C,C+\alpha_{2}-\alpha_{1})$。同理当$y^{(1)}$和$y^{(2)}$同号时有$L=max(0,\alpha_{2}+\alpha_{1}-C),R=min(C,\alpha_{2}+\alpha_{1})$。
首先定义$u=w^{T}x+b$
将$\alpha_{1},\alpha_{2}$带入$W(\alpha)$中得到:
$W(\alpha)=\frac{1}{2}(k_{11}\alpha_{1}^{2}+k_{22}\alpha_{2}^{2})+sk_{12}\alpha_{1}\alpha_{2}+y^{(1)}\alpha_{1}v_{1}+y^{(2)}\alpha_{2}v_{2}-\alpha_{1}-\alpha_{2}+P$
其中:
(1)$s=y^{(1)}y^{(2)}$
(2)$v_{1}=\sum_{i=3}^{n}y^{(i)}\alpha_{i}k_{1i}=u_{1}-b-y^{(1)}\alpha_{1}^{old}k_{11}-y^{(2)}\alpha_{2}^{old}k_{12}$
(3)$v_{2}=\sum_{i=3}^{n}y^{(i)}\alpha_{i}k_{2i}=u_{2}-b-y^{(1)}\alpha_{1}^{old}k_{12}-y^{(2)}\alpha_{2}^{old}k_{22}$
由于$y^{(1)}\alpha_{1}+y^{(2)}\alpha_{2}=y^{(1)}\alpha_{1}^{old}+y^{(2)}\alpha_{2}^{old}=\xi$
两边同时乘以$y^{(1)}$,得到$\alpha_{1}+s\alpha_{2}=\alpha_{1}^{old}+s\alpha_{2}^{old}=y^{(1)}\xi=T$
所以$\alpha_{1}=T-s\alpha_{2}$,将其带入$W(\alpha)$,得到$W(\alpha)=\frac{1}{2}(k_{11}(T-s\alpha_{2})^{2}+k_{22}\alpha_{2}^{2})+sk_{12}(T-s\alpha_{2})\alpha_{2}+y^{(1)}(T-s\alpha_{2})v_{1}+y^{(2)}\alpha_{2}v_{2}-(T-s\alpha_{2})-\alpha_{2}+P$
其实这是一个关于$\alpha_{2}$的二次函数,在一阶导数等于0的地方取得最小值,一阶导数为:$\frac{\partial W}{\partial \alpha_{2}}=-sk_{11}(T-s\alpha_{2})+k_{22}\alpha_{2}+sk_{12}(T-s\alpha_{2})-k_{12}\alpha_{2}-y^{(2)}v_{1}+y^{(2)}v_{2}+s-1=0$
移项得:$\alpha_{2}(k_{11}+k_{22}-2k_{12})=s(k_{11}-k_{12})T+y^{(2)}(v_{1}-v_{2})+1-s$
将$v_{1},v_{2}$带入得:$\alpha_{2}(k_{11}+k_{22}-2k_{12})=\alpha_{2}^{old}(k_{11}+k_{22}-2k_{12})+y^{(2)}(u_{1}-u_{2}+y^{(2)}-y^{(1)})$
令:
(1)$\eta =k_{11}+k_{22}-2k_{12}$
(2)$E_{1}=u_{1}-y^{(1)}$
(3)$E_{2}=u_{2}-y^{(2)}$
那么有:
$\alpha_{2}^{new}=\alpha_{2}^{old}+\frac{y^{(2)}(E_{1}-E_{2})}{\eta }$
这里就求出了新的$\alpha_{2}$。需要注意的是如果$\alpha_{2}$不在上面求出的[L,R]区间,要做一下裁剪。
由$y^{(1)}\alpha_{1}+y^{(2)}\alpha_{2}=y^{(1)}\alpha_{1}^{old}+y^{(2)}\alpha_{2}^{old}$可得:
$\alpha_{1}^{new}=\alpha_{1}^{old}+y^{(1)}y^{(2)}(\alpha_{2}^{old}-\alpha_{2}^{new})$
最后更新b
$b=\left\{\begin{matrix} b_{1} & 0<\alpha_{1}<C\\
b_{2} & 0<\alpha_{2}<C\\
\frac{1}{2}(b_{1}+b_{2}) & other
\end{matrix}\right.$
其中
$b_{1}=b-E_{1}-y^{(1)}(\alpha_{1}^{new}-\alpha_{1}^{old})k_{11}-y^{(2)}(\alpha_{2}^{new}-\alpha_{2}^{old})k_{12}$
$b_{2}=b-E_{2}-y^{(1)}(\alpha_{1}^{new}-\alpha_{1}^{old})k_{12}-y^{(2)}(\alpha_{2}^{new}-\alpha_{2}^{old})k_{22}$
这样更新b会迫使输入$x_{1}$时输出$y^{(1)}$,输入$x_{2}$时输出$y^{(2)}$
from numpy import *
import operator
from time import sleep
import numpy as np;
from svmplatt import *;
import matplotlib.pyplot as plt
class PlattSVM(object):
def __init__(self):
self.X = []
self.labelMat = []
self.C = 0.0
self.tol = 0.0
self.b = 0.0
self.kValue=0.0
self.maxIter=10000
self.svIndx=[]
self.sptVects=[]
self.SVlabel=[]
def loadDataSet(self,fileName):
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split(‘\t‘)
self.X.append([float(lineArr[0]), float(lineArr[1])])
self.labelMat.append(float(lineArr[2]))
self.initparam()
def kernels(self,dataMat,A):
m,n=shape(dataMat)
K=mat(zeros((m,1)))
for j in range(m):
delta=dataMat[j,:]-A
K[j]=delta*delta.T
K=exp(K/-1*self.kValue**2)
return K
def initparam(self):
self.X = mat(self.X)
self.labelMat = mat(self.labelMat).T
self.m = shape(self.X)[0]
self.lambdas = mat(zeros((self.m,1)))
self.eCache = mat(zeros((self.m,2)))
self.K = mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i] = self.kernels(self.X,self.X[i,:])
def randJ(self,i):
j=i
while(j==i):
j = int(random.uniform(0,self.m))
return j
def clipLambda(self,aj,H,L):
if aj > H: aj = H
if L > aj: aj = L
return aj
def calcEk(self,k):
return float(multiply(self.lambdas,self.labelMat).T*self.K[:,k] + self.b) - float(self.labelMat[k])
def chooseJ(self,i,Ei):
maxK = -1; maxDeltaE = 0; Ej = 0
self.eCache[i] = [1,Ei]
validEcacheList = nonzero(self.eCache[:,0].A)[0]
if (len(validEcacheList)) > 1:
for k in validEcacheList:
if k == i: continue
Ek = self.calcEk(k)
deltaE = abs(Ei - Ek)
if (deltaE > maxDeltaE):
maxK = k; maxDeltaE = deltaE; Ej = Ek
return maxK, Ej
else:
j = self.randJ(i)
Ej = self.calcEk(j)
return j, Ej
def innerLoop(self,i):
Ei = self.calcEk(i)
if ((self.labelMat[i]*Ei < -self.tol) and (self.lambdas[i] < self.C)) or ((self.labelMat[i]*Ei > self.tol) and (self.lambdas[i] > 0)):
j,Ej = self.chooseJ(i, Ei)
lambdaIold = self.lambdas[i].copy(); lambdaJold = self.lambdas[j].copy();
if (self.labelMat[i] != self.labelMat[j]):
L = max(0, self.lambdas[j] - self.lambdas[i])
H = min(self.C, self.C + self.lambdas[j] - self.lambdas[i])
else:
L = max(0, self.lambdas[j] + self.lambdas[i] - self.C)
H = min(self.C, self.lambdas[j] + self.lambdas[i])
if L==H: return 0
eta = 2.0 * self.K[i,j] - self.K[i,i] - self.K[j,j]
if eta >= 0: return 0
self.lambdas[j] -= self.labelMat[j]*(Ei - Ej)/eta
self.lambdas[j] = self.clipLambda(self.lambdas[j],H,L)
self.eCache[j] = [1,self.calcEk(j)]
if (abs(self.lambdas[j] - lambdaJold) < 0.00001): return 0
self.lambdas[i] += self.labelMat[j]*self.labelMat[i]*(lambdaJold - self.lambdas[j])
self.eCache[i] = [1,self.calcEk(i)]
b1 = self.b - Ei- self.labelMat[i]*(self.lambdas[i]-lambdaIold)*self.K[i,i] - self.labelMat[j]*(self.lambdas[j]-lambdaJold)*self.K[i,j]
b2 = self.b - Ej- self.labelMat[i]*(self.lambdas[i]-lambdaIold)*self.K[i,j] - self.labelMat[j]*(self.lambdas[j]-lambdaJold)*self.K[j,j]
if (0 < self.lambdas[i]) and (self.C > self.lambdas[i]): self.b = b1
elif (0 < self.lambdas[j]) and (self.C > self.lambdas[j]): self.b = b2
else: self.b = (b1 + b2)/2.0;
return 1
else: return 0
def train(self): #full Platt SMO
step = 0
entireflag = True; lambdaPairsChanged = 0
while (step < self.maxIter) and ((lambdaPairsChanged > 0) or (entireflag)):
lambdaPairsChanged = 0
if entireflag:
for i in range(self.m):
lambdaPairsChanged += self.innerLoop(i)
step += 1
else:
nonBoundIs = nonzero((self.lambdas.A > 0) * (self.lambdas.A < self.C))[0] for i in nonBoundIs: lambdaPairsChanged += self.innerLoop(i) step += 1 if entireflag: entireflag = False elif (lambdaPairsChanged == 0): entireflag = True self.svIndx = nonzero(self.lambdas.A>0)[0]
self.sptVects = self.X[self.svIndx]
self.SVlabel = self.labelMat[self.svIndx]
def scatterplot(self,plt):
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(shape(self.X)[0]):
if self.lambdas[i] != 0:
ax.scatter(self.X[i,0],self.X[i,1],c=‘green‘,marker=‘s‘,s=50)
elif self.labelMat[i] == 1:
ax.scatter(self.X[i,0],self.X[i,1],c=‘blue‘,marker=‘o‘)
elif self.labelMat[i] == -1:
ax.scatter(self.X[i,0],self.X[i,1],c=‘red‘,marker=‘o‘)
svm = PlattSVM()
svm.C=70
svm.tol=0.001
svm.maxIter=2000
svm.kValue= 3.0
svm.loadDataSet(‘nolinear.txt‘)
svm.train()
print(svm.svIndx)
print(shape(svm.sptVects)[0])
print("b:",svm.b)
svm.scatterplot(plt)
plt.show()
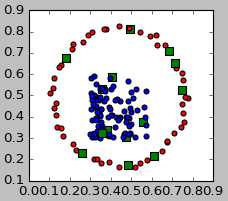
实验结果
标签:png under cli turn lambda 最小值 abs tor amp
原文地址:http://www.cnblogs.com/jianglangcaijin/p/6374064.html