标签:pre div 输入 include 题解 i++ csharp using void
[BZOJ2820]YY的GCD
试题描述
输入
输出
输入示例
2 10 10 100 100
输出示例
30 2791
数据规模及约定
T = 10000
N, M <= 10000000
题解
枚举公约素数 p,那么有
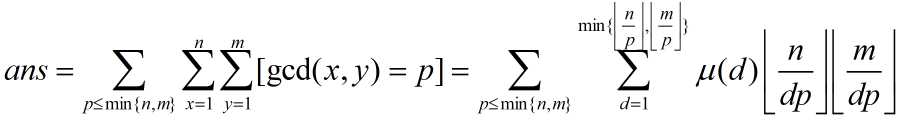
令 T = dp,并交换一下枚举顺序,得到
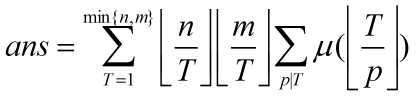
于是我们只需要预处理出
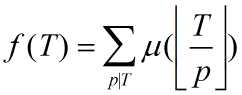
的前缀和,就可以 O(sqrt(n)) 回答每次询问了。
我们暴力枚举每个质数 p,然后更新 p 的倍数位置上的值,得到 f(T)(复杂度为 O(n / ln(n) * log(n))),然后 O(n) 求前缀和即可。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 10000010
#define LL long long
int prime[maxn], cp, mu[maxn], f[maxn], sf[maxn];
bool vis[maxn];
void init() {
mu[1] = 1;
for(int i = 2; i < maxn; i++) {
if(!vis[i]) prime[++cp] = i, mu[i] = -1;
for(int j = 1; i * prime[j] < maxn && j <= cp; j++) {
vis[i*prime[j]] = 1;
if(i % prime[j] == 0){ mu[i*prime[j]] = 0; break; }
mu[i*prime[j]] = -mu[i];
}
}
for(int i = 1; i <= cp; i++)
for(int j = 1; prime[i] * j < maxn; j++) f[j*prime[i]] += mu[j];
for(int i = 1; i < maxn; i++) sf[i] = sf[i-1] + f[i];
return ;
}
int main() {
init();
int T = read();
while(T--) {
int n = read(), m = read();
if(n > m) swap(n, m);
LL ans = 0;
for(int i = 1, lst; i <= n; i = lst + 1) {
lst = min(n / (n / i), m / (m / i));
ans += (LL)(n / i) * (m / i) * (sf[lst] - sf[i-1]);
}
printf("%lld\n", ans);
}
return 0;
}
标签:pre div 输入 include 题解 i++ csharp using void
原文地址:http://www.cnblogs.com/xiao-ju-ruo-xjr/p/7109372.html