标签:[1] running anaconda otl 线性代数 block evel pen 理解

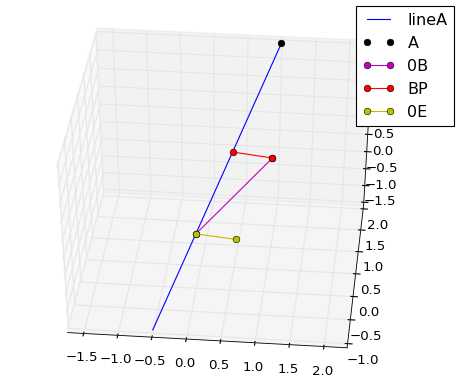
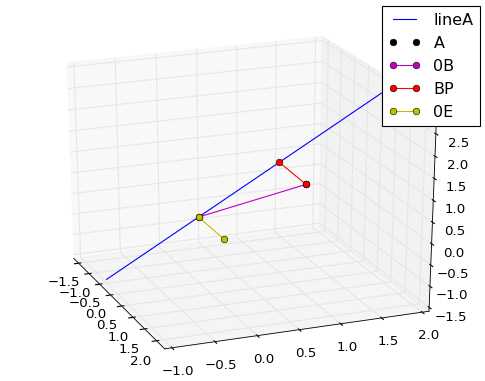
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D A=np.array([[1],[2],[3]]) B=np.array([[1],[1],[1]]) x=np.linspace(-0.5,1,10) x.shape=(1,10) xx=A.dot(x) C=A.T.dot(B) AA=np.linalg.inv(A.T.dot(A)) P=A.dot(AA).dot(C) E=B-P fig = plt.figure() ax = fig.add_subplot(111,projection=‘3d‘) ax.plot(xx[0,:],xx[1,:],xx[2,:],label="lineA") ax.plot(A[0],A[1],A[2],‘ko‘,label="A") ax.plot([0,B[0]],[0,B[1]],[0,B[2]],‘m-o‘,label="0B") ax.plot([B[0][0],P[0][0]],[B[1][0],P[1][0]],[B[2][0],P[2][0]],‘r-o‘,label="BP") ax.plot([0,E[0]],[0,E[1]],[0,E[2]],‘y-o‘,label="0E") ax.legend() ax.axis(‘equal‘) plt.show()
因为是三维图么,所以扭了一下多截了一张(笑):

import numpy as np
import matplotlib.pyplot as plt
import copy
# 产生一个方波(x,y)
x = np.linspace(-10,10,300)
y=[]
for i in np.cos(x):
if i>0:
y.append(0)
else:
y.append(2)
y=np.array(y)
def projection(A,b):
####
# return A*inv(AT*A)*AT*b
####
AA = A.T.dot(A)
w=np.linalg.inv(AA).dot(A.T).dot(b)
print(w)
return A.dot(w)
def fourier(x,y,N):
A = []
for i in x:
A.append(copy.deepcopy([]))
for j in range(N):
A[-1].append(np.sin((j + 1) * i))
A[-1].append(np.cos((j + 1) * i))
A[-1].append(1)
b = y.T
yw = projection(np.array(A),b)
return yw
# write Your code, Fourier function
plt.plot(x,y,color=‘g‘,label=‘origin‘)
plt.plot(x,fourier(x,y,3),color=‘r‘,label=‘3‘)
plt.plot(x,fourier(x,y,8),color=‘b‘,label=‘8‘)
plt.plot(x,fourier(x,y,23),color=‘k‘,label=‘23‘)
plt.legend()
plt.axis(‘equal‘)
plt.show()
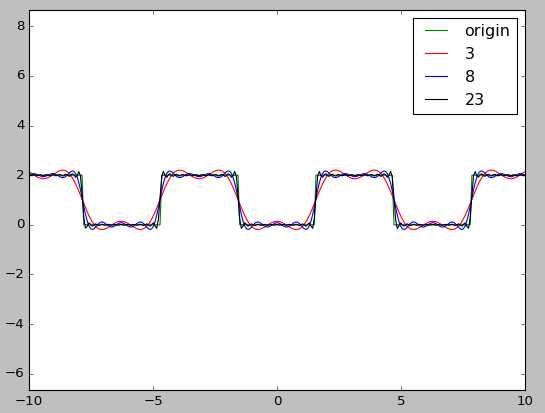
从输出图可以直观看出来项数越多拟合效果越好:

import numpy as np
import copy
import matplotlib.pyplot as plt
from matplotlib import animation
A=np.array([[3,1],[2,4]])/4.0
# write Your code
fig = plt.figure()
ax = fig.add_subplot(111)
line1, = ax.plot([],[],c=‘r‘)
line2, = ax.plot([],[],c=‘b‘)
ax.axis(‘equal‘)
ax.set_xlim(-2,2)
ax.set_ylim(-2,2)
ax.set_xticks(np.linspace(-2,2,5))
ax.set_yticks(np.linspace(-2,2,5))
ax.grid(True)
def data():
point_num = 100
x = np.cos(np.linspace(0,2 * np.pi,point_num))
y = np.sin(np.linspace(0,2 * np.pi,point_num))
rot_x,rot_y = copy.deepcopy([]),copy.deepcopy([])
int_x,int_y = copy.deepcopy([]),copy.deepcopy([])
for i in range(point_num):
rot_x.append(A.dot([x[i],y[i]])[0])
rot_y.append(A.dot([x[i],y[i]])[1])
int_x.append(x[i])
int_y.append(y[i])
yield (rot_x,rot_y,int_x,int_y)
def update(data):
line1.set_xdata(data[0])
line1.set_ydata(data[1])
line2.set_xdata(data[2])
line2.set_ydata(data[3])
return line1,line2
def init():
line1.set_data([],[])
line2.set_data([],[])
return line1,line2
ani = animation.FuncAnimation(fig,update,data,init_func=init,interval=100,repeat=False)
plt.show()
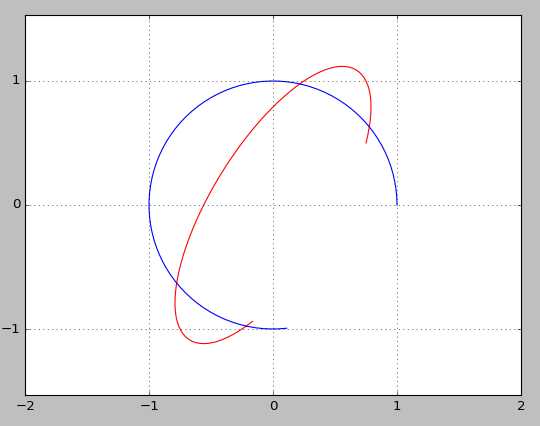
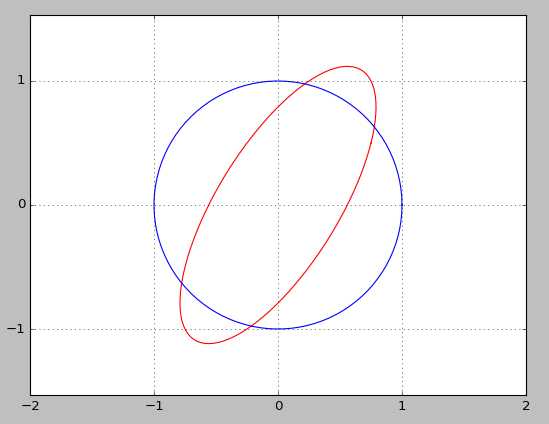
这是个动画,所以我截了两张图来表示,可以看到同一变换矩阵对不同方向的单位向量放缩长度并不相同,是个椭圆形:

import numpy as np
import matplotlib.pyplot as plt
import time
def time_cost(f):
def _f(*arg, **kwarg):
start = time.clock()
a=f(*arg,**kwarg)
end = time.clock()
print(f.__name__,"run cost time is ",end-start)
return a
return _f
@time_cost
def fib_opt_seq(seq):
return [fib_opt(i) for i in seq]
def fib_opt(n):
a,b,i=0,1,0
while i<n:
a,b=b,a+b
i+=1
else:
#print(b)
return b
import random
#seq = [random.randint(800,1000) for i in xrange(1000)]
seq = range(1000)
a=fib_opt_seq(seq)
# write Your code fib_eig_seq function
A = np.array([[1,1],[1,0]])
eigval,eigvect = np.linalg.eig(A)
S_inv = np.linalg.inv(eigvect)
@time_cost
def fib_eig_seq(seq):
return [fib_eig(i) for i in seq]
def fib_eig(n):
af = (np.diag(eigval)**(n+1)).dot(S_inv)
#print((eigvect.dot(af)).dot(np.array([[1],[0]]))[1])
return (eigvect.dot(af)).dot(np.array([[1],[0]]))[1]
b=fib_eig_seq(seq)
Python 3.5.2 |Anaconda 4.2.0 (64-bit)| (default, Jul 5 2016, 11:41:13) [MSC v.1900 64 bit (AMD64)]
Type "copyright", "credits" or "license" for more information.
IPython 5.1.0 -- An enhanced Interactive Python.
? -> Introduction and overview of IPython‘s features.
%quickref -> Quick reference.
help -> Python‘s own help system.
object? -> Details about ‘object‘, use ‘object??‘ for extra details.
PyDev console: using IPython 5.1.0fib_opt_seq run cost time is 0.08637829184750435
fib_eig_seq run cost time is 0.01634134003747284
上面对比了传统的递归方式生成斐波那契数列方式,一般来说随着数量的上升,使用矩阵速度更快。

import numpy as np
A = np.array([[ 0.8 , 0.1],
[ 0.2 , 0.9]])
N_year = 1000
x=np.array([3200,
4000])
def hw_3_5(a,x,n):
eigval, eigvact = np.linalg.eig(a)
res = (eigvact.dot((np.diag(eigval)**n).dot(np.linalg.inv(eigvact)).dot(x.T)))
print(res)
return res
hw_3_5(A,x,N_year)
IPython 5.1.0 -- An enhanced Interactive Python.
? -> Introduction and overview of IPython‘s features.
%quickref -> Quick reference.
help -> Python‘s own help system.
object? -> Details about ‘object‘, use ‘object??‘ for extra details.
PyDev console: using IPython 5.1.0
Running C:/Projects/python3_5/homework/hw_3-5_demo.py
[ 2400. 4800.]
虽然求解都类似,但是这是个收敛的差分方程,把100年换成1000年结果还是2400和4800。

再写程序的时候发现作业资料给的数据载入包并不能用(也许是python版本的问题),对debug不是很感兴趣,所以索性使用了tensorflow中提供的Mnist数据集调用方法了。
思路有一点偏差,我看了答案,其原意是把N幅数据组成N*(28*28)的二维矩阵,对这个矩阵进行降维,然后在绘图时还原整个矩阵,再在矩阵中进行子图分割;我理解成把每幅小图独自降维保存了,不过除了使我的程序麻烦了一点之外没什么其他影响:
import os
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
print(os.getcwd())
os.environ[‘TF_CPP_MIN_LOG_LEVEL‘] = ‘3‘
batch_size = 10
mnist = input_data.read_data_sets(‘../../Mnist_data/‘, one_hot=True)
batch_xs,batch_ys = mnist.train.next_batch(batch_size)
print(batch_xs.shape)
# write Your code
def pca(data,k=0.5):
# data 原始的图片
# k是保留特征值的百分比
# return 返回降维后重建的图片
res = np.empty_like(data).reshape(batch_size, 28, 28)
rec = np.empty_like(res)
data = data.reshape(batch_size, 28, 28)
for i in range(batch_size):
cov = np.cov(data[i])
eigVal, eigVact = np.linalg.eig(cov)
print(cov.shape, eigVal.shape, eigVact.shape)
for j in range(len(eigVal) - 1):
# print(sum(eigVal[:j]),sum(eigVal[:]),sum(eigVal[:j])/sum(eigVal[:]))
if sum(eigVal[:j])/sum(eigVal[:]) > k:
print(‘提取前面‘,j, ‘个特征‘)
break
# res[i] = eigVact[:,:j].T.dot(data[i].T)# np.dot(eigVact[:j],data[i].T)
a = eigVact#[:,:j]
b = data[i]
print(a.shape,b.shape)
res[i] = np.dot(b, a)
rec[i] = np.dot(res[i],a.T)
f,a = plt.subplots(2,batch_size,figsize=(10,2))
for i in range(batch_size):
a[0][i].imshow(data[i],‘gray‘)
a[0][i].set_xticks([])
a[0][i].set_yticks([])
a[1][i].imshow(rec[i].reshape(28,28),‘gray‘)
a[1][i].set_xticks([])
a[1][i].set_yticks([])
# N = 20
recon_data = pca(batch_xs)
# show_pic(data[:N,:],recon_data[:N,:])
保留占比50%的特征值后压缩(上行是原图,下行是压缩后的图片):

保留占比90%的特征值后压缩(上行是原图,下行是压缩后的图片):

 直观来看90%对50%似乎提升不大,不过查看90%和50%保留的特征个数就卡以发现,其实两者的特征数目相差不大,基本上都在5个以下(总数应该是28个左右),也就是说PCA压缩是有道理的——实际上图片的大量信息被保存在极少的几个特征上了。
直观来看90%对50%似乎提升不大,不过查看90%和50%保留的特征个数就卡以发现,其实两者的特征数目相差不大,基本上都在5个以下(总数应该是28个左右),也就是说PCA压缩是有道理的——实际上图片的大量信息被保存在极少的几个特征上了。
标签:[1] running anaconda otl 线性代数 block evel pen 理解
原文地址:http://www.cnblogs.com/hellcat/p/7141421.html