标签：技术 量化 ges logs 算法 微积分 导数 alt idt
我们可以将成本函数的两个条件情形压缩为一个情形：
注意到当y=1，那么
=0也就是说没有效果。
当y=0，那么
=0。
我们可以完全写出我们的全部成本函数如下：
矢量化实现：
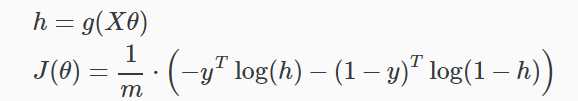
梯度下降
请记住，梯度下降的一般形式是：
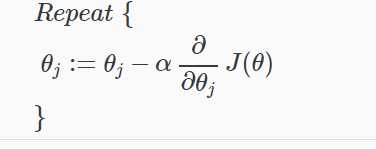
利用微积分可以求出导数的部分：
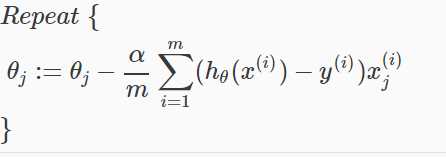
注意，这个算法与我们在线性回归中使用的算法是一样的。我们仍然必须同时更新θ中的所有值
矢量化实现：
标签：技术 量化 ges logs 算法 微积分 导数 alt idt
原文地址：http://www.cnblogs.com/zhengzhe/p/7225724.html
