标签:范围 iostream letter 线段树 neu 高度 white std 树状
这节课难度超级大啊,基本上都是省选+NOI的题。
例1:
Time Limit: 10 Sec Memory Limit: 64 MB Submit: 1868 Solved: 1075 [Submit][Status][Discuss]
除了在3个格子中都放满炮的的情况外,其它的都可以.
100%的数据中N,M不超过100 50%的数据中,N,M至少有一个数不超过8 30%的数据中,N,M均不超过6
那么怎么样才能通过全部分呢?状压dp比较耗时的原因是枚举每一行的状态用时太多,我们每次都要考虑每一列放或不放,要考虑2^m次,但是这道题只要求计数啊,所以我们完全不必记录每一行到底怎么放,我们只需要考虑有几行怎么放就可以了,也就是说,我们不必考虑每一行具体的怎么放,我们只需要考虑每一行中有多少列不放,放一个,放两个即可。
那么设f[i][j][k]为前i行中有j列放1个,有k列放2个的方案数,可以发现每一行最多只能放两个,那么这些炮可以不放,放在只放了一个的列里,放在没有放的列里,并考虑一下放几个,状态转移方程就出来了,不过这个方程实在是太复杂,可以看代码理解:
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <queue> using namespace std; const int mod = 9999973; int n, m,ans; long long f[110][110][110]; int C(int x) { return x * (x - 1) / 2; } int main() { scanf("%d%d", &n, &m); f[0][0][0] = 1; for (int i = 1; i <= n; i++) { for (int j = 0; j <= m; j++) { for (int k = 0; k <= m; k++) { f[i][j][k] = (f[i][j][k] + f[i - 1][j][k]) % mod; //不放 if (j >= 1) f[i][j][k] = (f[i][j][k] + f[i - 1][j - 1][k] * (m - j + 1 - k) % mod) % mod; //在没有的列上放一个 if (k >= 1) f[i][j][k] = (f[i][j][k] + f[i - 1][j + 1][k - 1] * (j + 1) % mod) % mod; //在只有一个的列上放一个 if (j >= 2) f[i][j][k] = (f[i][j][k] + f[i - 1][j - 2][k] * C(m - j + 2 - k) % mod) % mod; //在没有的列上放二个 if (k >= 2) f[i][j][k] = (f[i][j][k] + f[i - 1][j + 2][k - 2] * C(j + 2) % mod) % mod; //在只有一个的列上放二个 if (k >= 1) f[i][j][k] = (f[i][j][k] + f[i-1][j][k - 1] * j * (m - j - k + 1) % mod ) % mod; //在有一个和没有的列上放二个 } } } for (int i = 0; i <= m; i++) for (int j = 0; j <= m; j++) ans = (ans + f[n][i][j]) % mod; printf("%d\n", ans % mod); //while (1); return 0; }
总结:有时候状态记录的不要太精细,特别是求方案数的,我们只需要记录怎么放的行数和列数就能做出来就完全不需要记录到底是哪一行怎么放。
例2:
分析:这个原题的数据范围是非常非常小的,只不过这里出的有点丧心病狂.这道题有点像背包,我们可以设f[i][j][k]表示前i首歌中用了y张唱片并且当前唱片长度用了k的最多放的歌曲的数目,转移就很好办了,如果ai > k,那么只能不放或者试试放在上一个唱片里。如果ai <= k,那么可以不放或者放,状态转移长这样: 时间复杂度O(nmt),由于包含了t,完美爆掉.
时间复杂度O(nmt),由于包含了t,完美爆掉.
那么我们想,能不能不要记录这个k,也就是只要前两维,这样就可以保证复杂度里没有t,但是如果不要第三维,我们怎么知道当前唱片用了多少长度呢?我们完全可以开一个二元组,记录答案和当前的k,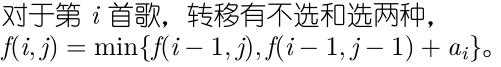 ,这里的加法是唱片数和k同时相加,这样我们就不需要枚举k了,成功解决,复杂度O(nm).
,这里的加法是唱片数和k同时相加,这样我们就不需要枚举k了,成功解决,复杂度O(nm).
总结:我们完全可以把设计的状态中的某一维放进答案里记录,这样可以精简状态.不过前提是这一维能通过其它的维度推出来.这个做法主要是应用于状态设计中某一维过大,用来减少复杂度.
例3:
方伯伯在自己的农田边散步,他突然发现田里的一排玉米非常的不美。
这排玉米一共有N株,它们的高度参差不齐。
方伯伯认为单调不下降序列很美,所以他决定先把一些玉米拔高,再把破坏美感的玉米拔除掉,使得剩下的玉米的高度构成一个单调不下降序列。
方伯伯可以选择一个区间,把这个区间的玉米全部拔高1单位高度,他可以进行最多K次这样的操作。拔玉米则可以随意选择一个集合的玉米拔掉。
问能最多剩多少株玉米,来构成一排美丽的玉米。
第1行包含2个整数n,K,分别表示这排玉米的数目以及最多可进行多少次操作。
第2行包含n个整数,第i个数表示这排玉米,从左到右第i株玉米的高度ai。
输出1个整数,最多剩下的玉米数。
1 < N < 10000,1 < K ≤ 500,1 ≤ ai ≤5000
分析:这道题就是求一个LIS,只不过多了一个拔高的限制,那么在原有的LISdp方程中加一个维度就好了,用f(i,j) 表示以第 i 株玉米结尾它被拔高了 j 次的最长序列长度。
f(i,j) = max{f(p,q) + 1}(0 ≤ p < i,0 ≤ q ≤ j,a [p] + q ≤a[i] + j)
现在来讲一讲为什么有第二个限制,可以发现每次操作的右端点都必须是n,为什么呢?因为如果不是n,那么它就不会对右边有贡献,只会对左边有贡献,是n的话不会影响对左边的贡献,而p<i,所以一定有第二个限制。
不过这个算法复杂度是O(n^2*k^2)的,会超时,我们该怎么优化呢?
可以发现这就是维护一个二维前缀最大值,对于前缀的操作可以用前缀和,也可以用树状数组,不过这个不满足区间加减,所以我们用二维树状数组来维护就可以了。不过在操作的时候要倒序操作,以免状态重复转移.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <queue> using namespace std; int n, k,a[10010],c[10010][510],maxn,ans; void add(int x, int y, int v) { for (int i = x; i <= maxn; i += i & -i) for (int j = y; j <= k + 1; j += j & -j) c[i][j] = max(c[i][j], v); } int sum(int x, int y) { int res = 0; for (int i = x; i; i -= i & -i) for (int j = y; j; j -= j & -j) res = max(res, c[i][j]); return res; } int main() { scanf("%d%d", &n, &k); for (int i = 1; i <= n; i++) { scanf("%d", &a[i]); maxn = max(maxn, a[i]); } maxn += k; //因为可能会被增加k次,所以上限+k for (int i = 1; i <= n; i++) for (int j = k; j >= 0; j--) { int t = sum(a[i] + j, j + 1) + 1; //至于为什么要j+1,因为我们调用不能出现0,否则会死循环 add(a[i] + j, j + 1, t); ans = max(t, ans); } printf("%d\n", ans); return 0; }
总结:一些dp可以利用数据结构来加速优化,例如遇到区间可以考虑线段树,前缀和,树状数组......
不过还可以考虑另外一种优化:
f(i,j) = max{f(p,q) + 1}(0 ≤ p < i,0 ≤ q ≤ j,a [p] + q ≤a [i] + j)。
f(i,j ? 1) = max{f(p,q) + 1}(0 ≤ p < i,0 ≤ q < j, a [p] + q < a [i] + j)。
可以发现f[i][j]从f[i][j-1]转移而来限制条件只是多了一个q=j或a[p] + q = a[i] + j,那么我们维护多个一维树状数组,就能够通过查询前缀最大值来求解.
总结:对于有限制条件的,我们可以通过其相邻状态的限制条件的不同来转移,可能会有意想不到的效果,不过似乎这种优化很少见...
标签:范围 iostream letter 线段树 neu 高度 white std 树状
原文地址:http://www.cnblogs.com/zbtrs/p/7351930.html