标签:启发式 密码 读取数据 更新 baidu 概述 class 位置 二分
一.svm概述
svm是一种二分类模型,学习策略是通过间隔最大化来实现分类的目的,最终转化为了凸二次规划求解,即:
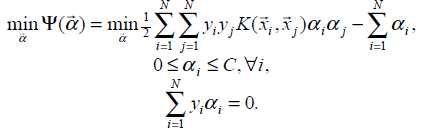
的确我们可以单纯的通过求解凸二次规划问题来获得答案,但是当训练样本量很大时,这些算法就会变的低效,从上面的公式就可以直观看出,有多少样例就有多少乘子,如何高效求解拉格朗日乘子成为了关键——smo。
浏览了很多博文总结一下具体的求解过程(smo):
1.寻找违背KKT条件的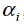 ,即:
,即:
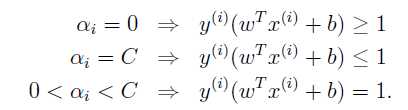
其中:
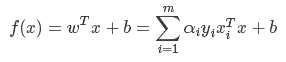
2.寻找第二个乘子,通过:max|E1-E2|
3.求解约束前的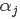 ,公式为:
,公式为:
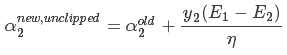 其中,
其中,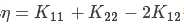 ,Ei=f(xi)-yi
,Ei=f(xi)-yi
4.对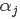 进行约束:
进行约束:
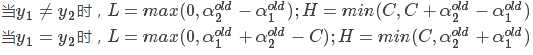
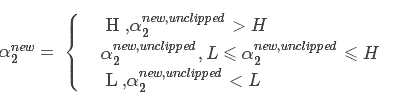
5.通过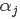 求解
求解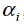 :
:
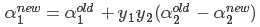
6.对b的更新
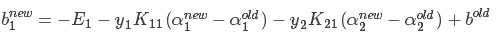
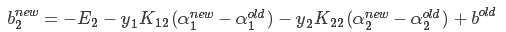
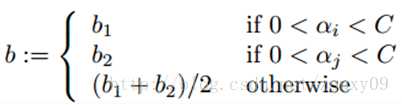
7.启发式迭代具体方法:后续补充
二.python实现
#利用svm求解逻辑回归,然后画图(详细版)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#读取数据
traindata=pd.read_csv("E:\\caffe\\study\\3_data.csv")
traindata=traindata.iloc[0:100,:]
#准备函数
def ui(No,traindata,alpha,b):#求ui
a=0
for i in range(len(traindata)):
a=a+alpha[i]*traindata.iloc[i,2]*(traindata.iloc[i,0]*traindata.iloc[No,0]+traindata.iloc[i,1]*traindata.iloc[No,0])
a=a+b
return a
def Ei(No,traindata,alpha,b):#求Ei=ui-yi
a=ui(No,traindata,alpha,b)-traindata.iloc[No,2]
return a
def alpha2(i,traindata,alpha,b):#找第二个alpha2在alpha向量中的位置,通过max|Ei-Ej|
ei=Ei(i,traindata,alpha,b)
a=0
c=0
for j in range(len(traindata)):
ej=Ei(j,traindata,alpha,b)
bi=abs(ei-ej)
if bi>a:
a=bi
c=j
return c
def eta(traindata,i,j):#求分母eta
a=traindata.iloc[i,0]**2+traindata.iloc[i,1]**2+traindata.iloc[j,0]**2+traindata.iloc[j,1]**2-2*(traindata.iloc[i,0]*traindata.iloc[j,0]+traindata.iloc[i,1]*traindata.iloc[j,1])
return a
def alpha2new(traindata, i,j,alpha,b):#求alpha2new,这里直接做约束
a=alpha[j]+traindata.iloc[j,2]*(Ei(i,traindata,alpha,b)-Ei(j,traindata,alpha,b))/eta(traindata,i,j)
if traindata.iloc[i,2]==traindata.iloc[j,2]:
L=0
H=alpha[i]+alpha[j]
if a>H:
return H
elif a<L:
return L
else:
return a
else:
L=np.array([0,alpha[j]-alpha[i]]).max()
if a<L:
return L
else:
return a
def alpha1new(traindata, i,j,alpha,b):#把alpha2new带进去求alpha1new
a=alpha[i]+traindata.iloc[i,2]*traindata.iloc[j,2]*(alpha[j]-alpha2new(traindata, i,j,alpha,b))
return a
def bnew(traindata, i,j,alpha,b):#更新b
ei=Ei(i,traindata,alpha,b)
ej=Ei(j,traindata,alpha,b)
yi=traindata.iloc[i,2]
yj=traindata.iloc[j,2]
alphai=alpha1new(traindata, i, j, alpha, b)
alphaj=alpha2new(traindata, i,j,alpha,b)
b1=b-ei-yi*(alphai-alpha[i])*(traindata.iloc[i,0]**2+traindata.iloc[i,1]**2)-yj*(alphaj-alpha[j])*(traindata.iloc[i,0]*traindata.iloc[j,0]+traindata.iloc[i,1]*traindata.iloc[j,1])
b2=b-ej-yi*(alphai-alpha[i])*(traindata.iloc[i,0]*traindata.iloc[j,0]+traindata.iloc[i,1]*traindata.iloc[j,1])-yj*(alphaj-alpha[j])*(traindata.iloc[j,0]**2+traindata.iloc[j,1]**2)
if alphai>0:
return b1
elif alphaj>0:
return b2
else:
return (b1+b2)/2
#上面的所有函数只需要加载一下即可,重点在下面的实际运行
alpha = np.zeros(len(traindata)) # 初始化alpha向量,零向量,长度为数据的长度
alphav = alpha.copy()#alphav相当于经过一次更新后的alpha向量,目的在于下面运行的时候会和更新前的alpha做比较
b = 0 # 初始化b为0
for i in range(len(alpha)): # 对所有违反kkt的alpha做更新,最后输出alpha为更新后的alpha,中间的b也是更新好的
if (alpha[i]==0 and traindata.iloc[i,2]*ui(i,traindata,alpha,b)>=1)+(alpha[i]>0 and traindata.iloc[i,2]*ui(i,traindata,alpha,b)<=1)==0:
j = alpha2(i, traindata, alpha, b)
t = alpha2new(traindata, i, j, alpha, b)
if t >= 0:
alphav[j] = t
alphav[i] = alpha1new(traindata, i, j, alpha, b)
if alphav[i]!=alpha[i]:
b = bnew(traindata, i, j, alpha, b)
alpha = alphav
#下面是用来临时检验alpha和b的结果是否正确,方法是计算出w,初始化一组x,将w,b带入计算y,看y的结果是否合理,可以和原始数据作图对比
w=np.zeros(2)#初始化w
for i in range(len(alpha)):
w=w+alpha[i]*traindata.iloc[i,2]*np.array(traindata.iloc[i,:2])
w=list(w)
x=[1,10]#初始化x
y=[((-1)*b-w[0]*plot_x[0])/w[1],(b-w[0]*plot_x[1])/w[1]]#计算y
附原始数据:链接:http://pan.baidu.com/s/1miT3Dzi 密码:cipe
标签:启发式 密码 读取数据 更新 baidu 概述 class 位置 二分
原文地址:http://www.cnblogs.com/danning13/p/7468518.html