标签:random nbsp 过程 git 比较 ati str 基础 再计算
git地址: https://github.com/JEAN330/nangua
| psp | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planing | 计划 | 10 | 10 |
| ? Estimate | ? 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 600 | 900 |
| ? Analysis | ? 需求分析(包括学习新技术) | 60 | 120 |
| ? Design Spec | ? 生成设计文档 | 20 | 20 |
| ? Design Review | ? 设计复审 (和同事审核设计文档) | 10 | 10 |
| ? Coding Standard | ? 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| ? Design | ? 具体设计 | 30 | 45 |
| ? Coding | ? 具体编码 | 350 | 500 |
| ? Coding Review | ? 代码复审 | 60 | 100 |
| ? Test | ? 测试(自我测试,修改代码,提交修改) | 60 | 85 |
| Reporting | 报告 | 130 | 190 |
| ? Test Report | ? 测试报告 | 100 | 150 |
| ? Size Measurement | ? 计算工作量 | 10 | 10 |
| ? Postmortem & Process Improvement Plan | ? 事后总结, 并提出过程改进计划 | 20 | 30 |
| 合计 | 740 | 1100 |
在第一次看到这道题时,我就觉得这道题挺复杂的,果然,有一个附加功能我还没有实现。先不考虑括号的功能,这道题对于我来说的难点有以下几点:
1、如何实现真分数与整数或真分数与真分数的计算
2、如何随机生成一个合理的表达式
3、如何将表达式计算出来
4、如何将用户输入的结果与正确答案进行比较
这些问题的解决方法如下:
1、分数以分子、分母的形式保存在二维数组中,整数以分子、1的形式保存在二维数组中,即将所有的数都以分数的形式保存,并用分数的计算方法计算。
2、随机生成m个分数与n个整数,随机生成m+n-1个运算符,数的排列顺序随机排序,并将数和符号依次排列
3、将表达式转换为逆波兰表达式再计算,虽然之前学过,但是已经忘得差不多了,所以还是需要重新学习
4、将用户输入的结果和正确答案以字符串的形式进行比较
1、真分数生成
public static int[] fraction() { //定义一个真分数
int x=(int)(Math.random()*10)+1; //随机生成10以内的不为0的分子分母
int y=(int)(Math.random()*10)+1;
if(x<=y){
return gcd(x,y);
}
else{
return gcd(y,x);
}
}
2、分数化简
public static int[] gcd(int x,int y){ //辗转相除得到最简分数
int temp,x1=x,y1=y;
if(x>=y) //假分数化简
{
while(x!=y){
temp=y;
if((x-y)<=temp){ //比较减数与被减数的大小,将大的值赋予x,小的值赋予y
y=x-y;
x=temp;
}
else{
x=x-y;
y=temp;
}
}
}
else //真分数化简
{
while(x!=y){
temp=x;
if((y-x)<=temp){
x=y-x;
y=temp;
}
else{
y=y-x;
x=temp;
}
}
}
int[] array={x1/x,y1/y};
return array;
}
3、随机生成表达式
public static int[] display(int n,int m,int[] a,int[][] b,int[] op){
int i,j,k,l;
int[] order=new int[20]; //为整数和真分数排序
for(i=0,j=0,k=0,l=0;k<m+n;) //随机排列整数和真分数
{
int x=(int)(Math.random()*2);
if(x==0&&i<n)
{
order[k]=0;
System.out.print(a[i]);
if(k<m+n-1)
{
switch(op[l])
{
case 0:System.out.print("+");break;
case 1:System.out.print("-");break;
case 2:System.out.print("*");break;
case 3:System.out.print("÷");break;
}
l++;
}
k++;
i++;
}
if(x==1&&j<m){
order[k]=1;
System.out.print(b[j][0]+"/"+b[j][1]);
if(k!=m+n-1)
{
switch(op[l])
{
case 0:System.out.print("+");break;
case 1:System.out.print("-");break;
case 2:System.out.print("*");break;
case 3:System.out.print("÷");break;
}
l++;
}
j++;
k++;
}
}
System.out.print("=");
return order;
}
4、转换为逆波兰表达式
public static int[] res(int[] a,int b[][],int[] op,int[] order,int n,int m){ //将中缀表达式转换为后缀表达式
stack<Integer> stack = new arraystack<Integer>();
int i=0,j=0,o,k,l;
int[] arr=new int[2];
int[][] c=new int[30][2];
stack.push(op[0]);
if(order[0]==0) //将整数以整数/1的形式存入数组,便于之后的计算
{
c[0][0]=a[i];
c[0][1]=1;
i++;
}
else{
c[0][0]=b[0][0];
c[0][1]=b[0][1];
j++;
}
for(k=1,l=1,o=1;k<n+m;k++){ //将中缀表达式按照逆波兰表达的顺序存入二维数组
if(order[k]==0){
c[o][0]=a[i++];
c[o][1]=1;
o++;
}
else{
c[o][0]=b[j][0];
c[o++][1]=b[j++][1];
}
if(l<(m+n-1)){
while(!stack.isEmpty()&&precedence(stack.peek(),op[l])>=0){
switch(stack.pop()){
case 0:c[o][0]=0;c[o++][1]=0;break;
case 1:c[o][0]=0;c[o++][1]=1;break;
case 2:c[o][0]=0;c[o++][1]=2;break;
case 3:c[o][0]=0;c[o++][1]=3;break;
}
}
stack.push(op[l++]);
}
}
if(!stack.isEmpty()){
int length=stack.length();
for(i=0;i<length;i++){
switch(stack.pop()){
case 0:c[o][0]=0;c[o++][1]=0;break;
case 1:c[o][0]=0;c[o++][1]=1;break;
case 2:c[o][0]=0;c[o++][1]=2;break;
case 3:c[o][0]=0;c[o++][1]=3;break;
}
}
}
arr=calculate(c,n,m);
return arr;
}
5、计算
public static int[] calculate(int[][] c,int n,int m){
int i,w,x,y,z;
int[] arr=new int[2];
stack<Integer> stack = new arraystack<Integer>();
for(i=0;i<2*m+2*n-1;i++){
if(c[i][0]==0){
z=stack.pop();y=stack.pop();x=stack.pop();w=stack.pop();
switch(c[i][1]){
case 0:arr=cal(w,x,y,z,0);stack.push(arr[0]);stack.push(arr[1]);break;
case 1:arr=cal(w,x,y,z,1);stack.push(arr[0]);stack.push(arr[1]);break;
case 2:arr=cal(w,x,y,z,2);stack.push(arr[0]);stack.push(arr[1]);break;
case 3:arr=cal(w,x,y,z,3);stack.push(arr[0]);stack.push(arr[1]);break;
}
}
else{
stack.push(c[i][0]);
stack.push(c[i][1]);
}
}
arr[1]=stack.pop();
arr[0]=stack.pop();
return arr;
}
通过输入参数3,可以自动生成3个算式

测试不同的方法,所得结果如下:
其中main()的测试中,默认用户输入值为0,且随机生成的算式个数为1000。
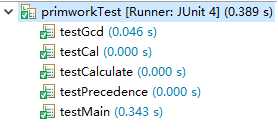
本次实验对我来说算是一个小小的考验,所完成的项目还有很多瑕疵,比如括号的功能没有实现,随机生成的数总是设置为正数,避免除数和分母为0的情况。并且只有在输入最简分数时才能判定为正确,未化简的情况以及带分数的情况都判定为错。而且从测试结果来看,当需要生成足够多的算式时,运行速度过慢,所以这次实验还有很多需要优化的地方,由于时间原因,只能仓促完成,但是之后的时间里我还是会继续完善这个项目,包括实现括号,提高项目性能等。这次实验我看到了我很多的缺点,基础知识薄弱,动手能力差,希望能在接下来的学习中继续提升自己。
标签:random nbsp 过程 git 比较 ati str 基础 再计算
原文地址:http://www.cnblogs.com/nanguaerzhi/p/7603330.html