标签:style blog http 使用 ar strong 2014 art 问题
之前我们在求Logistic回归时,用的是梯度上升算法,也就是要使得似然函数最大化,利用梯度上升算法,不断的迭代。这节课引出牛顿方法,它的作用和梯度上升算法的一样的,不同的是牛顿方法所需的迭代次数更少,收敛速度更快。
红色曲线是利用牛顿法迭代求解,绿色曲线是利用梯度下降法求解。
牛顿法:wiki
牛顿法(Newton‘s method)又称为牛顿-拉弗森方法(Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。方法使用函数
的泰勒级数的前面几项来寻找方程
的根。
首先,选择一个接近函数 零点的
零点的 ,计算相应的
,计算相应的 和切线斜率
和切线斜率 (这里
(这里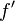 表示函数
表示函数 的导数)。然后我们计算穿过点
的导数)。然后我们计算穿过点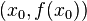 并且斜率为
并且斜率为 的直线和
的直线和 轴的交点的
轴的交点的 坐标,也就是求如下方程的解:
坐标,也就是求如下方程的解:

我们将新求得的点的 坐标命名为
坐标命名为 ,通常
,通常 会比
会比 更接近方程
更接近方程 的解。因此我们现在可以利用
的解。因此我们现在可以利用 开始下一轮迭代。迭代公式可化简为如下所示:
开始下一轮迭代。迭代公式可化简为如下所示:
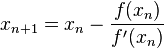
已经证明,如果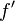 是连续的,并且待求的零点
是连续的,并且待求的零点 是孤立的,那么在零点
是孤立的,那么在零点 周围存在一个区域,只要初始值
周围存在一个区域,只要初始值 位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果
位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果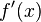 不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
from:http://blog.csdn.net/luoleicn/article/details/6527049
在上面讨论的是2维情况,高维情况的牛顿迭代公式是:
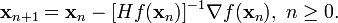
其中H是hessian矩阵,定义为:
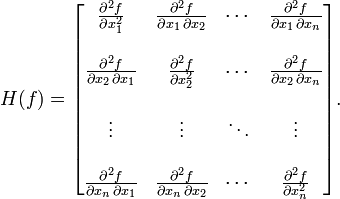
高维情况依然可以用牛顿迭代求解,但是问题是Hessian矩阵引入的复杂性,使得牛顿迭代求解的难度大大增加,但是已经有了解决这个问题的办法就是Quasi-Newton methond,不再直接计算hessian矩阵,而是每一步的时候使用梯度向量更新hessian矩阵的近似。
【cs229-Lecture4】Newton’s method
标签:style blog http 使用 ar strong 2014 art 问题
原文地址:http://www.cnblogs.com/XBWer/p/3964312.html