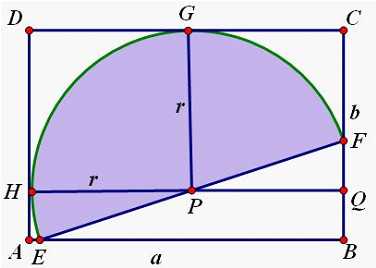
图 1
如图1,设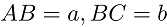 ,本解法只讨论当长宽比小于2,即
,本解法只讨论当长宽比小于2,即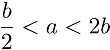 时的情况,因为其它情况极易得到解法.
时的情况,因为其它情况极易得到解法.
记最大半圆圆心为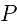 ,直径两个端点
,直径两个端点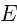 在线段
在线段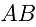 上,
上,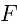 在线段
在线段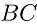 上,可以证明半圆与
上,可以证明半圆与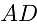 和
和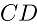 相切,设切点分别为
相切,设切点分别为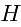 和
和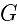 .过点
.过点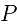 作
作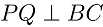 ,垂足为
,垂足为 ,设半圆半径为
,设半圆半径为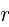 ,显然
,显然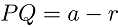 ,
,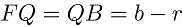 ,在
,在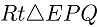 中应用勾股定理得
中应用勾股定理得
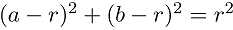 ,
,
化简得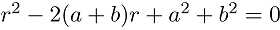 ,解出
,解出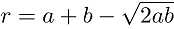 ,显然
,显然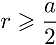
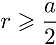 且
且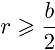 ,这就表明在这种情况下,最
,这就表明在这种情况下,最 大半圆的半径不是边长的一半.
大半圆的半径不是边长的一半.
标签:logs es2017 情况下 font 勾股定理 justify 半径 image enter

图 1
如图1,设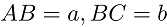 ,本解法只讨论当长宽比小于2,即
,本解法只讨论当长宽比小于2,即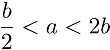 时的情况,因为其它情况极易得到解法.
时的情况,因为其它情况极易得到解法.
记最大半圆圆心为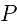 ,直径两个端点
,直径两个端点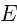 在线段
在线段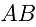 上,
上,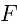 在线段
在线段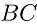 上,可以证明半圆与
上,可以证明半圆与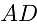 和
和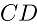 相切,设切点分别为
相切,设切点分别为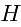 和
和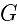 .过点
.过点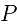 作
作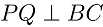 ,垂足为
,垂足为 ,设半圆半径为
,设半圆半径为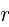 ,显然
,显然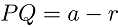 ,
,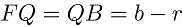 ,在
,在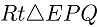 中应用勾股定理得
中应用勾股定理得
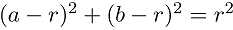 ,
,
化简得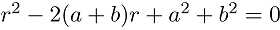 ,解出
,解出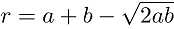 ,显然
,显然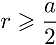
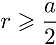 且
且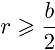 ,这就表明在这种情况下,最
,这就表明在这种情况下,最 大半圆的半径不是边长的一半.
大半圆的半径不是边长的一半.
标签:logs es2017 情况下 font 勾股定理 justify 半径 image enter
原文地址:http://www.cnblogs.com/shukiang/p/8045766.html