题目描述
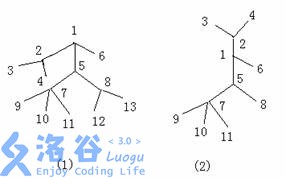
对于一棵树,我们可以将某条链和与该链相连的边抽出来,看上去就象成一个毛毛虫,点数越多,毛毛虫就越大。例如下图左边的树(图 1 )抽出一部分就变成了右边的一个毛毛虫了(图 2 )。
输入输出格式
输入格式:
在文本文件 worm.in 中第一行两个整数 N , M ,分别表示树中结点个数和树的边数。
接下来 M 行,每行两个整数 a, b 表示点 a 和点 b 有边连接( a, b ≤ N )。你可以假定没有一对相同的 (a, b) 会出现一次以上。
输出格式:
在文本文件 worm.out 中写入一个整数 , 表示最大的毛毛虫的大小。
输入输出样例
输出样例#1:
11
说明
40% 的数据, N ≤ 50000
100% 的数据, N ≤ 300000
解题思路:树形DP
f[i]表示以i为根的子树的最长长度。
link[i]表示与i相连的点的个数
那么对于某个节点i,他对答案的贡献为:
由i扩展出去的最长链长度+由i扩展出去的次长链长度+与i相连的点的个数(注意更新时节点的重复)
#include<iostream>
#include<cstdio>
#include<algorithm>
#define DB double
#include<cmath>
#define pi 3.1415926535898
using namespace std;
inline int read()
{
int x=0,w=1;char ch=getchar();
while(!isdigit(ch)){if(ch==‘-‘) w=-1;ch=getchar();}
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-‘0‘,ch=getchar();
return x*w;
}
const int N=300009;
struct node{
int u,v,ne;
}e[N*2];
int n,h[N],tot;
void add(int u,int v)
{
tot++;e[tot]=(node){u,v,h[u]};h[u]=tot;
}
int m,link[N],f[N],ans;
void dfs(int x,int fa)
{
int l1=-1,l2=-1;
for(int i=h[x];i;i=e[i].ne)
{
int rr=e[i].v;
if(rr==fa) continue;
dfs(rr,x);
if(f[rr]>l2)
{
if(f[rr]>l1) l2=l1,l1=f[rr];
else l2=f[rr];
}
f[x]=max(f[x],f[rr]+link[x]-1);
}
ans=max(ans,l1+l2+link[x]-1);
}
int main()
{
n=read();m=read();
for(int i=1;i<=m;++i)
{
int x,y;x=read();y=read();
add(x,y);add(y,x);
link[x]++;link[y]++;
}
for(int i=1;i<=n;++i) f[i]=1;
dfs(1,0);
printf("%d",ans);
return 0;
}
勿忘初心!
