
没有三点共线
这题的思想来源于JOI2011-2012春季训练合宿Day2T2,原题是个大毒瘤题,这题作为原题要用到的的一个结论而存在
点有两种颜色,先考虑对所有点做凸包,假如凸包上的颜色段大于$2$段,那么无解

因为连线一定在凸包内部,所以上图中红色和蓝色不可能不相交而连接起来
为了做这题,首先我们描述一个过程:$solve(A,B,C)$,其中$B,C$颜色相同且已经直接或间接地被连起来,$A$是另一种颜色,这个过程可以把$\triangle ABC$内的所有点按对应颜色连起来且连线不相交
solve($A$,$B$,$C$){
if($\exists P$ in $\triangle ABC$ and $P.color$==$A.color$){
link($A$,$P$);
solve($B$,$A$,$P$);
solve($C$,$A$,$P$);
solve($P$,$B$,$C$);
}else{
link all $P$ in $\triangle ABC$ with $B$ or $C$
}
}
代码应该挺容易懂的,如果找到和$A$同色的点就可以递归做,否则把所有三角形内的点用某种方式与$B,C$连接起来,我用的方法是把所有点极角排序,然后把每个点和左下角的点连起来
要处理两种情况
①凸包上所有点同色
把凸包上连一圈,然后再内部随便找一个不同颜色的点$P$,以它为中心绕着调用$solve(P,hull_i),hull_{i+1}$
②凸包上有两段颜色
把凸包上相同颜色的连起来,然后如图所示
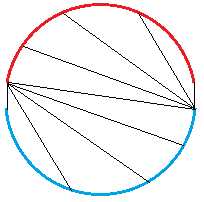
就是找到每段颜色的第一个点和另一边的每一条边组成的三角形调用$solve$就可以了
因为没有三点共线,所以这样做一定可以得出答案
东舰共荣还行==
#include<stdio.h>
#include<algorithm>
using namespace std;
#define ll long long
#define inf 2147483647
struct point{
int x,y,bl,id;
double ang;
void get(){
if(x==0)
ang=(y==0)?-inf:inf;
else
ang=y/(double)(x);
}
point(int a=0,int b=0){x=a;y=b;}
}p[3010],h[3010],t[3010];
int N,n,m,stk[3010];
bool cmp1(point a,point b){return a.ang<b.ang;}
bool cmp2(point a,point b){return a.id<b.id;}
int nex(int x){
if(x<N)return x+1;
return 1;
}
point operator-(point a,point b){
return point(a.x-b.x,a.y-b.y);
}
ll cross(point a,point b){
return a.x*(ll)b.y-a.y*(ll)b.x;
}
int conv(){
sort(p+1,p+n+m+1,cmp1);
int i,top;
top=2;
stk[1]=1;
stk[2]=2;
for(i=3;i<=n+m;i++){
while(top>1&&cross(p[stk[top]]-p[stk[top-1]],p[i]-p[stk[top]])<0)top--;
top++;
stk[top]=i;
}
for(i=1;i<=top;i++)h[i]=p[stk[i]];
sort(p+1,p+n+m+1,cmp2);
return top;
}
struct edge{
int x,y;
edge(int a=0,int b=0){x=a;y=b;}
}e[3010];
int tot;
void add(int x,int y){
tot++;
e[tot]=edge(x,y);
}
bool intri(point a,point b,point c,point d){
if(cross(b-a,c-b)<0)swap(b,c);
return cross(d-b,a-d)>0&&cross(d-c,b-d)>0&&cross(d-a,c-d)>0;
}
void gao(int a,int b,int c){
int i,e,mx,my;
for(i=1;i<=n+m;i++){
if(p[i].bl==p[a].bl&&intri(p[a],p[b],p[c],p[i])){
add(a,i);
gao(b,a,i);
gao(c,a,i);
gao(i,b,c);
return;
}
}
e=1;
t[1]=p[b];
for(i=1;i<=n+m;i++){
if(intri(p[a],p[b],p[c],p[i])){
e++;
t[e]=p[i];
}
}
mx=inf;
for(i=1;i<=e;i++){
if(t[i].x<mx||(t[i].x==mx&&t[i].y<my)){
mx=t[i].x;
my=t[i].y;
}
}
for(i=1;i<=e;i++){
t[i].x-=mx;
t[i].y-=my;
t[i].get();
}
sort(t+1,t+e+1,cmp1);
for(i=2;i<=e;i++)add(t[1].id,t[i].id);
}
int main(){
int i,mx,my,ct;
scanf("%d%d",&n,&m);
mx=inf;
for(i=1;i<=n+m;i++){
scanf("%d%d",&p[i].x,&p[i].y);
if(p[i].x<mx||(p[i].x==mx&&p[i].y<my)){
mx=p[i].x;
my=p[i].y;
}
p[i].id=i;
if(i>n)p[i].bl=1;
}
for(i=1;i<=n+m;i++){
p[i].x-=mx;
p[i].y-=my;
p[i].get();
}
N=conv();
ct=0;
for(i=1;i<=N;i++){
if(h[i].bl!=h[nex(i)].bl)ct++;
}
if(ct>2){
puts("touhou-kancolle war can not be avoided!");
return 0;
}
if(ct==0){
for(i=1;i<N;i++)add(h[i].id,h[i+1].id);
for(i=1;i<=n+m;i++){
if(p[i].bl!=h[1].bl){
mx=i;
break;
}
}
for(i=1;i<=N;i++)gao(mx,h[i].id,h[nex(i)].id);
}else{
for(i=1;h[i].bl==h[nex(i)].bl;i=nex(i));
for(i=nex(i);h[i].bl==h[nex(i)].bl;i=nex(i))add(h[i].id,h[nex(i)].id);
for(i=nex(i);h[i].bl==h[nex(i)].bl;i=nex(i))add(h[i].id,h[nex(i)].id);
mx=i;
for(i=nex(i);h[i].bl==h[nex(i)].bl;i=nex(i))gao(h[mx].id,h[i].id,h[nex(i)].id);
mx=i;
for(i=nex(i);h[i].bl==h[nex(i)].bl;i=nex(i))gao(h[mx].id,h[i].id,h[nex(i)].id);
}
for(i=1;i<=tot;i++){
if(p[e[i].x].bl==0)printf("%d %d\n",e[i].x,e[i].y);
}
for(i=1;i<=tot;i++){
if(p[e[i].x].bl==1)printf("%d %d\n",e[i].x-n,e[i].y-n);
}
}
