标签:highlight 成功 name car stdin ima png sdi return
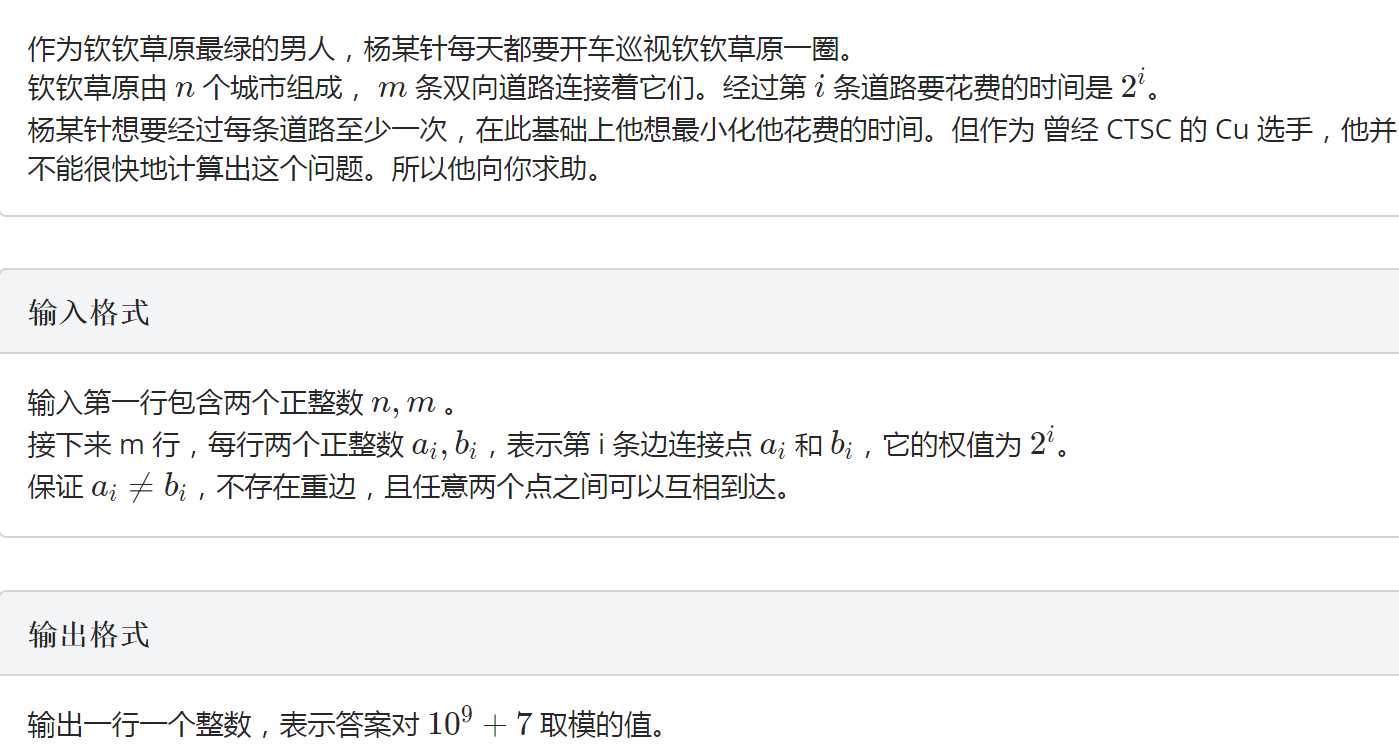
可以发现每条边只能选一次或者两次,并且最后每个点的度数(∑邻接边选的次数和)都是偶数(代表有欧拉回路)。
然后根据题意列一个 n 行 m+1 列的01矩阵,每一行代表一个异或方程组(每个点的度数是偶数),每一列(除了最后一列)代表一个变量(每条边是不是选2次),最后一列0/1代表这个点目前的度数是偶数还是奇数。
最后我们要求的就是方程所有解中逆字典序最小的解。
乍一看肯定是毫无思路,但是做了 [HAOI2018] 反色游戏 之后,就感觉这两个东西还是有点点共性的。
我们高斯消元的过程肯定是 i = 1 to m ,找到a[j][i]不为0的所有j(如果没有这样的j就忽略掉),把第二个j开始的所有行都异或最小的j那一行。
但是对于这种特殊的矩阵,我们可以发现异或的过程就相当于把两个点合并,或者说就是并查集合并的过程:合并成功的话那这个变量(代表原图中的一条边)就不是自由元;否则就是自由元。。。。
我们肯定是想让权值大的边是自由元,这样就可以不选了,肯定更优。
所以我们就跑一遍最小生成树,找出不是自由元的边,然后现在就只有一组解了(n个方程n-1个变量,保证有解,因为任意图的度数和肯定是偶数),dfs扫一遍就可以了。。。。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<ctime>
#define ll long long
using namespace std;
const int maxn=500005,ha=1e9+7;
inline int read(){
int x=0; char ch=getchar();
for(;!isdigit(ch);ch=getchar());
for(;isdigit(ch);ch=getchar()) x=x*10+ch-‘0‘;
return x;
}
inline void ADD(int &x,int y){ x+=y; if(x>=ha) x-=ha;}
int n,m,d[maxn],ans,p[maxn],hd[maxn];
int to[maxn*2],ne[maxn*2],val[maxn*2],num;
inline void addline(int x,int y,int z){ to[++num]=y,ne[num]=hd[x],hd[x]=num,val[num]=z;}
int getf(int x){ return p[x]==x?x:(p[x]=getf(p[x]));}
void dfs(int x,int fa){
for(int i=hd[x];i;i=ne[i]) if(to[i]!=fa){
dfs(to[i],x);
if(d[to[i]]) d[x]^=1,ADD(ans,val[i]);
}
}
int main(){
// freopen("carcar.in","r",stdin);
// freopen("carcar.out","w",stdout);
scanf("%d%d",&n,&m);
int u,v;
for(int i=1;i<=n;i++) p[i]=i;
for(int i=1,fa,fb,now=2;i<=m;ADD(now,now),i++){
ADD(ans,now);
u=read(),v=read(),d[v]^=1,d[u]^=1;
fa=getf(u),fb=getf(v);
if(fa!=fb){
p[fa]=fb;
addline(u,v,now);
addline(v,u,now);
}
}
dfs(1,0);
printf("%d\n",ans);
return 0;
}
标签:highlight 成功 name car stdin ima png sdi return
原文地址:https://www.cnblogs.com/JYYHH/p/9159682.html