标签:time lex strong 统计学习 for 连续 ati 全连接 旅行商
典型的深度学习(Deep Learning)模型就是很深层的神经网络模型,因此可以说深度学习就是神经网络的再发展。神经网络最早追溯到1950s提出的感知机,可以算是神经网络发展的第一次高潮;但在1969年,Marvin Minsky和Seymour Papert指出单层的神经网络无法解决非线性问题,使得神经网络的研究陷入的“冰河期”;1983年John Hopfield利用神经网络获得旅行商这个NP问题的当时最优解,引起轰动。Rumelhart等人重新发明BP,使BP算法迅速走红。在1990s,随着统计学习和SVM的兴起,神经网络梯度消失等问题,使得神经网络再次陷入沉寂。NIPS会议甚至一度不接受神经网络相关的论文;2009,随着GPU技术的出现,使得模型的训练不在那么耗时。2011年,神经网络在语音辨识取得了较大的成功。2012年,AlexNet模型在Image Net上获得第一名,神经网络在“深度学习”的名义下,又迎来发展期。
神经元是神经网络中的最基本的单元,其结构如图1-1所示,具体计算过程如(1)
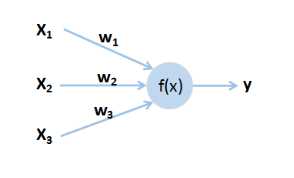
图1-1 神经元

其中,x是神经元的输入,w是x对应的权重,f(x)是激活函数,y是神经元输出,b为偏置。
神经元跟神经元之间的连接方式有很多种,不同的连接方式就构成了不同的模型结构。全连接前馈神经网络结构如图1-2所示。全连接的意思就是对于当前神经元,神经元跟前一层所有的神经元都进行连接,而且不进行跨层连接,同一层的神经元间不进行连接。
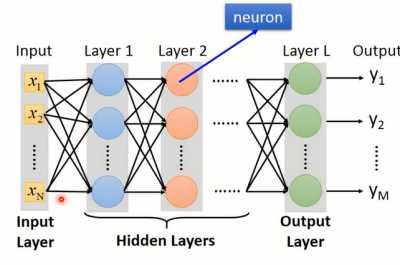
图1-2 全连接神经网络
其中,第一层输入的X={x1,x2,...xN}为输入层(Input Layer),最后一层Layer L为输出层(Output Layer),其余的称作隐藏层(Hidden Layer)。在训练模型之前,我们会初始化模型参数,也就是模型中每个神经元的w和b。在给定输入的X={x1,x2,...xN}后,神经网络的每个神经元都按照(1)进行计算,就得到了Y={y1,y2,yM}。这个计算过程称为前向传播。
在给定神经网络结构和初始化参数后(如图1-3所示),就需要进行前向传播计算。假定激活函数为sigmoid,sigmoid函数形式为(2)
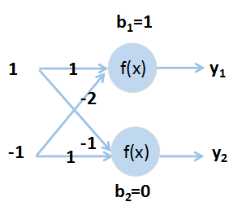
图1-3 前向传播计算

y1,y2的具体计算过程如下

使用(3)的计算过程,为了对整个前向传播进行简介表示,会采用矩阵操作的形式进行表示,具体计算如(4)

因此,对于多层的神经网络,整个前向传播就是多进行(4)这样的矩阵操作。此外,在进行矩阵运算的时候,可以采用GPU进行加速计算。
Hornik在1989年证明了一个包含足够多隐层的前馈神经网络能够以任意精度逼近任意复杂的连续函数。因此,神经网络可可以看做是任意函数的逼近器。但是,隐藏层的层数以及每一个层神经元的数量如何设计却还没有解决方法。在传统的机器学习方法中,通常需要进行特征转换,找到一组较好的特征。但在深度学习中,就并不需要找一组特别好的特征。如在进行影像辨识,可以直接将像素作为输入,然后进行训练。但是,深度学习也创造了另一个问题,就是模型应该如何设计!因此,如果你能够很容易提取特征,往往可能并不需要DL;但在一些特征不容易去提取,使用DL可以获得较好的结果。如,DL在NLP领域并没有取得像语音辨识一样的巨大进步。
如果以分类为例的话,那么最终的输出层往往会使用softmax来代替。而损失函数采用的则是交叉熵(Cross Entropy),整个结构如图1-4所示
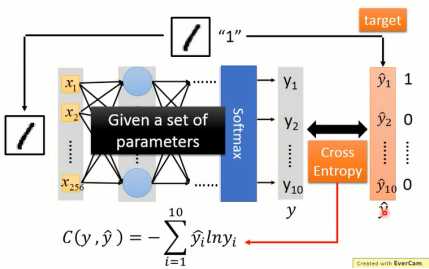
图1-4 神经网络评估函数
在确定损失函数后,就需要最小化损失函数值。而采用的方法也就是梯度下降,但是在计算百万级别的参数时,需要一种有效计算梯度的方法,这种方法就是反向传播(简称BP)。
[2]《机器学习》-周志华
标签:time lex strong 统计学习 for 连续 ati 全连接 旅行商
原文地址:https://www.cnblogs.com/MrPan/p/9495215.html