标签:如何 比赛 names http font bubuko 注意 family hat
终于知道为什么比赛的时候B题没人做了……
+传送门+(这是beta版的)
· 【描述】
数轴的正半轴上(>0,且垃圾位置相同)有n个垃圾,分别位于 x1,x2,...,xn 。有一个机器人在原点,每次可以移动一步。原点还有一个垃圾桶,机器人要把垃圾捡到垃圾桶里。机器人可以同时拿多个垃圾,当它拾起一个垃圾或者把它携带的所有垃圾丢到垃圾桶里时,需要消耗X点能量。且当机器人拿起k个垃圾时,每移动一个单位就需要消耗(1+k)2点能量。求出机器人把所有垃圾捡回垃圾桶所需要的最小能量。注意:机器人只能把垃圾丢进垃圾桶里,不能放在数轴的其他位置
· 【输入】
第一行输入n;第二行输入 n 个整数表示垃圾的位置,从左到右依次输入。
· 【输出】
机器人把所有垃圾捡到垃圾桶里的最小花费。
表面上其实看不出来这是一道结论题……
最重要的一个结论应该是只要找到一个"AA","BB" 相间的环就满足问题。可以用反证法:
①若环内连续A或B的个数小于1,则无法构成"AA"或者"BB";
②若环内连续A或B的个数超过2(>),则必然存在一个串,结尾为"ABBA"或"BAAB"无法构成;
so that? 其实已经得证了……
如何找满足条件的环?我们可以想象环是长这个样子的:
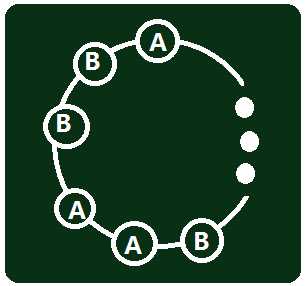
然后我们就会发现……除了用点集表示一个环,也可以用边集。
我们可以令连接"AA"或"BB"的边为0,连接"AB"的边为1(QwQ)。所以环就是10101010101……所以对于环上一个点,它在环上的两条边一定是一条1、一条0。
简单地,用DFS,从一个点出发,先走一条"1"边,再走一条"0"边,交替进行(或者先"0"边,然后"1"边)。非常的麻烦,并不想这么做。于是运用拆点的思想,将一个点u拆一个虚点u‘。原图有多条边以点u开始,令原图中边的结束点为v,当u,v标志相同时则我们将u连接v‘,v连接u‘,否则将u‘连到v,v‘连到u(单向)。
举个例子:
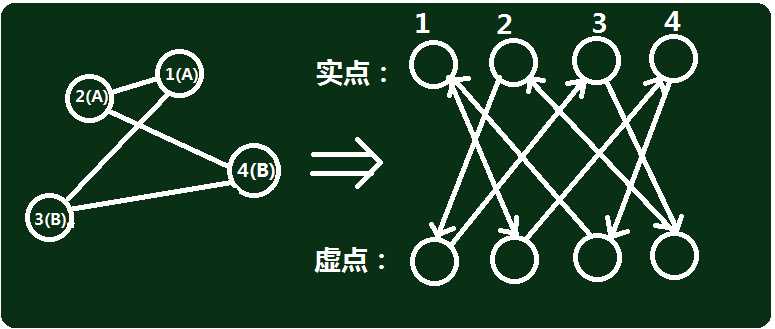
(有点乱不要在意TAT)
解释一下建图过程:拿点1来说
由于1->2是连接相同标志点的边("0"边),则建立 1->2‘ 和 2->1‘;由于 1->3 是连接不同标志点的边("1"边),则建立 1‘->3 和 3‘->1 。其他都是这样建的。二分图吗?right!
环 1->2->4->3->1 就是一个合法环,那么在新建的图上是怎样表现的? 1->2‘->4->3‘->1 ,二分图上找一个环?就是这样。用二分图,我们可以直接回避连续经过"1"边或"0"边,因为从实点出发到虚点,就会经过"0"边,而从虚点到实点就会经过"1"边,二分图上实点虚点交替经过。只要在二分图上找到一个环即可。
/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=int(2e5);
vector<int> lnk[2*N+5];
int n,m;
char fla[N+5];
int tag[2*N+5];
void DFS(int u){
tag[u]=1;
for(int i=0;i<lnk[u].size();i++){
int v=lnk[u][i];
if(tag[v]==0)
DFS(v);
if(tag[v]==1){
printf("Yes\n");
exit(0);
}
}
tag[u]=-1;
}
int main(){
scanf("%d%d%s",&n,&m,fla+1);
for(int i=0;i<m;i++){
int u,v;scanf("%d%d",&u,&v);
if(fla[u]==fla[v]){
lnk[u].push_back(v+n);
lnk[v].push_back(u+n);
}
else{
lnk[u+n].push_back(v);
lnk[v+n].push_back(u);
}
}
for(int i=1;i<=n;i++)
if(tag[i]==0)
DFS(i);
printf("No\n");
return 0;
}
- Lucky_Glass
【杂题总汇】AGC027 B - Garbage Collector
标签:如何 比赛 names http font bubuko 注意 family hat
原文地址:https://www.cnblogs.com/LuckyGlass-blog/p/9674230.html