标签:des style http color io os ar java for
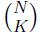 different plans.
different plans.4 1 2 10 1
14 36 30 8
题解及代码:
拿到题目的时候一直在想有什么组合的方法,或者是DP之类的可以由两个数推导到三个数等等,想了好一会也没什么思路。
之后想到异或的性质,因为最后的答案是要相加的,所以异或之后的每一位想要有值的话,那么我们必须保证进行异或的数字在当前位上的1个个数必须是奇数,想到这里,思路就有了。我们只需要求出每个数二进制表示形势下每一位1和0的个数,那么然后在求组合数就可以了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const long long mod=1e6+3;
long long C[1010][1010];
long long l[70],r[70];
long long num[70];
long long sum=0;
void init()
{
C[0][0]=1;
C[1][0]=C[1][1]=1;C[1][2]=0;
for(int i=2;i<=1000;i++)
{
C[i][0]=1;
for(int j=1;j<=i;j++)
C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
C[i][i+1]=0;
}
num[0]=1;num[1]=2;
for(int i=2;i<=62;i++)
{
num[i]=(num[i-1]*2)%mod;
}
}
int main()
{
init();
int n,color,k;
while(scanf("%d",&n)!=EOF)
{
sum=0;
memset(l,0,sizeof(l));
for(int i=1;i<=n;i++)
{
scanf("%d",&color);
sum+=color;
sum%=mod;
k=0;
while(color)
{
l[k++]+=(color&1);
color/=2;
}
}
printf("%I64d",sum);
for(int i=0;i<=62;i++)
{
r[i]=n-l[i];
}
for(int i=2;i<=n;i++)
{
sum=0;
for(int j=0;j<=62;j++)
{
if(l[j])
for(k=1;k<=i&&k<=l[j];k+=2)
{
//printf("%d %d %d,%d %d %d,%d \n",l[j],k,C[l[j]][k],r[j],n-k,C[r[j]][n-k],num[j]);
sum+=(C[l[j]][k]*C[r[j]][i-k]%mod*num[j])%mod;
sum%=mod;
}
}
printf(" %I64d",sum);
}
puts("");
}
return 0;
}
标签:des style http color io os ar java for
原文地址:http://blog.csdn.net/knight_kaka/article/details/39935149