码迷，mamicode.com
首页 > 编程语言 > 详细

test20181107 猴子排序

时间：2018-11-07 18:41:33      阅读：175      评论：0      收藏：0      [点我收藏+]

标签：cstring   names   name   十分   mod   space   stdout   git   pow   

题意

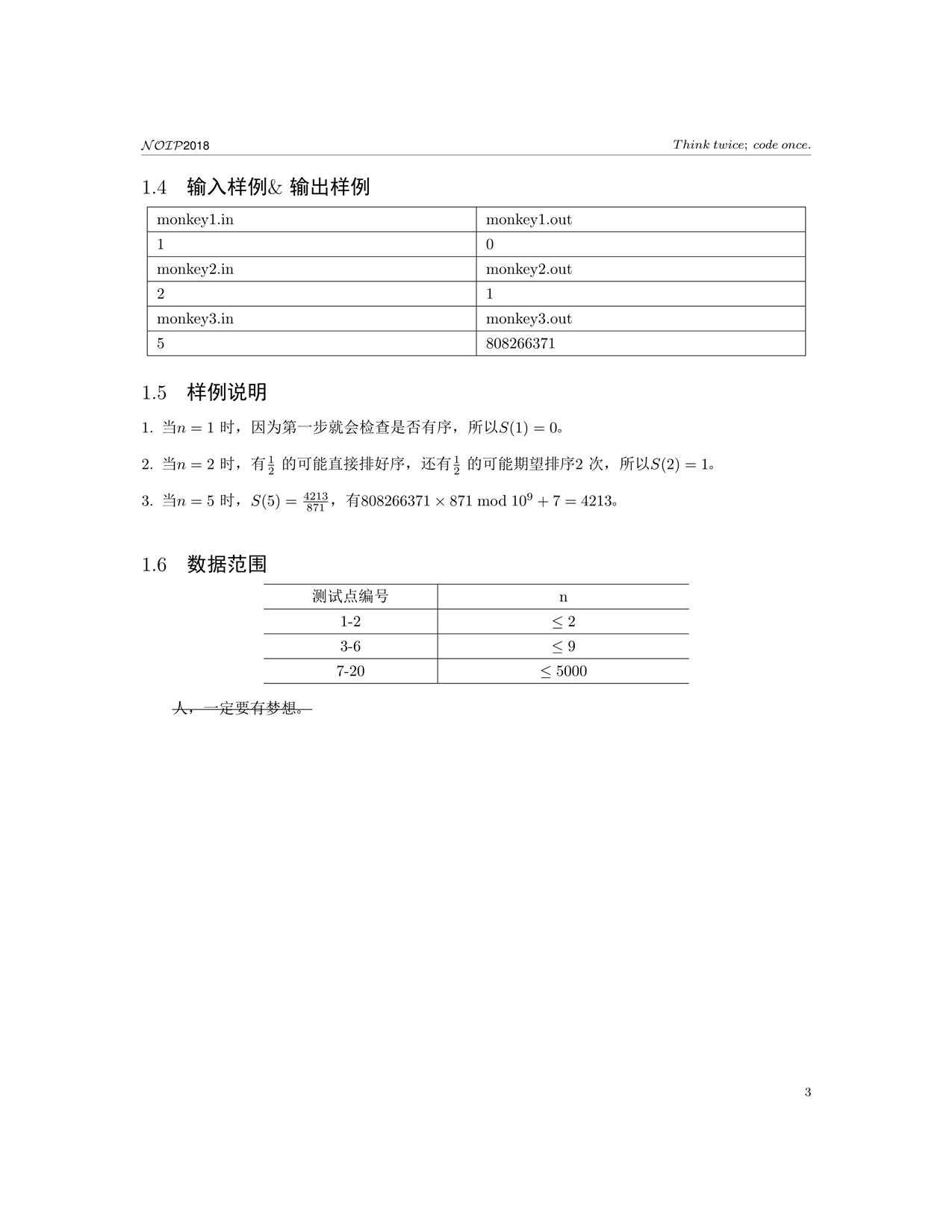
技术分享图片
技术分享图片

分析

考场做法

用\(s(n,i)\)表示长度为\(n\)的排列中出现\(i\)段连续块的方案数。

用隔板法枚举每块有哪些元素，减去由\(s(n,1) \sim s(n,i-1)\)中继续插板得到的多加的，得到
\[ s(n,i)=\binom{n-1}{i-1}-\sum_{j=1}^{i-1}\binom{n-1-(j-1)}{i-1-(j-1)}s(n,j) \]

然后设\(f(n)\)表示排列恰好分为\(n\)段连续块时所期望的步骤数，列出方程
\[ f(n)=\frac{\sum_{i=1}^{n}s(n,i)(f(i)+1)}{n!} \\frac{n!-s(n,n)}{n!}f(n)=\frac{\sum_{i=1}^{n-1}s(n,i)(f(i)+1)}{n!} \f(n)=\frac{\sum_{i=1}^{n-1}s(n,i)(f(i)+1)}{n!-s(n,n)} \]

最后统计答案
\[ ans=\frac{\sum_{i=1}^{n}s(i)f(i)}{n!} \]

这个算法的瓶颈在于每次算\(s(n,1) \sim s(n,n)\)的复杂度是\(O(n^2)\)的。这样整个算法的时间复杂度\(O(n^3)\)

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<set>
#include<map>
#include<queue>
#include<vector>
//#include<algorithm>
#include<string>
#define co const
#define il inline
#define rg register
template<class T>T read(T&x)
{
    T data=0;
    int w=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-')
            w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        data=data*10+ch-'0';
        ch=getchar();
    }
    return x=data*w;
}
using namespace std;
typedef long long ll;

co int MAXN=5e3+7,mod=1e9+7;
int fac[MAXN],ifac[MAXN];

int add(int x,int y)
{
    x+=y;
    return x>=mod?x-mod:x;
}

int sub(int x,int y)
{
    x-=y;
    return x<0?x+mod:x;
}

int mul(int x,int y)
{
    return (ll)x*y%mod;
}

int qpow(int x,int k)
{
    int res=1;
    while(k)
    {
        if(k&1)
            res=mul(res,x);
        x=mul(x,x),k>>=1;
    }
    return res;
}

int div(int x,int y)
{
    return mul(x,qpow(y,mod-2));
}

int binom(int n,int m)
{
    return mul(fac[n],mul(ifac[m],ifac[n-m]));
}

int f[MAXN],s[MAXN];

int main()
{
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
    int n;
    read(n);
    fac[0]=fac[1]=ifac[0]=ifac[1]=1;
    for(int i=2;i<MAXN;++i)
    {
        fac[i]=mul(i,fac[i-1]);
        ifac[i]=mul(mod-mod/i,ifac[mod%i]);
    }
    for(int i=2;i<MAXN;++i)
    {
        ifac[i]=mul(ifac[i],ifac[i-1]);
    }
    f[1]=0;
    for(int i=2;i<=n;++i)
    {
//      cerr<<"pro "<<i<<endl;
        for(int j=1;j<=i;++j)
        {
            s[j]=mul(binom(i-1,j-1),fac[j]);
            for(int k=1;k<j;++k)
                s[j]=sub(s[j],mul(binom(i-k,j-k),s[k]));
//          cerr<<j<<" s="<<s[j]<<endl;
        }
        for(int j=1;j<i;++j)
            f[i]=add(f[i],mul(s[j],add(f[j],1)));
        f[i]=add(f[i],s[i]);
        f[i]=div(f[i],sub(fac[i],s[i]));
    }
    int ans=0;
    for(int i=1;i<=n;++i)
        ans=add(ans,mul(s[i],f[i]));
    ans=mul(ans,ifac[n]);
    printf("%d\n",ans);
    return 0;
}

然后发现可以利用中间结果打表，耗时最多5000s，而我打完代码还剩三四十分钟的样子，不可能每个点跑到1s，所以就打了个表。

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<set>
#include<map>
#include<queue>
#include<vector>
//#include<algorithm>
#include<string>
#define co const
#define il inline
#define rg register
template<class T>T read(T&x)
{
    T data=0;
    int w=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-')
            w=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        data=data*10+ch-'0';
        ch=getchar();
    }
    return x=data*w;
}
using namespace std;
typedef long long ll;

co int MAXN=5e3+7,mod=1e9+7;
int fac[MAXN],ifac[MAXN];

il int add(rg int x,rg int y)
{
    x+=y;
    return x>=mod?x-mod:x;
}

il int sub(rg int x,rg int y)
{
    x-=y;
    return x<0?x+mod:x;
}

il int mul(rg int x,rg int y)
{
    return (ll)x*y%mod;
}

il int qpow(rg int x,rg int k)
{
    rg int res=1;
    while(k)
    {
        if(k&1)
            res=mul(res,x);
        x=mul(x,x),k>>=1;
    }
    return res;
}

il int div(rg int x,rg int y)
{
    return mul(x,qpow(y,mod-2));
}

il int binom(rg int n,rg int m)
{
    return mul(fac[n],mul(ifac[m],ifac[n-m]));
}

int f[MAXN],s[MAXN];

int main()
{
    freopen("t1chart.in","r",stdin);
    freopen("t1chart.out","w",stdout);
    int n;
    read(n);
    fac[0]=fac[1]=ifac[0]=ifac[1]=1;
    for(rg int i=2;i<MAXN;++i)
    {
        fac[i]=mul(i,fac[i-1]);
        ifac[i]=mul(mod-mod/i,ifac[mod%i]);
    }
    for(rg int i=2;i<MAXN;++i)
    {
        ifac[i]=mul(ifac[i],ifac[i-1]);
    }
    f[1]=0;
    printf("0,\n");
    for(rg int i=2;i<=n;++i)
    {
        cerr<<"pro "<<i<<endl;
        for(rg int j=1;j<=i;++j)
        {
            s[j]=mul(binom(i-1,j-1),fac[j]);
            for(rg int k=1;k<j;++k)
                s[j]=sub(s[j],mul(binom(i-k,j-k),s[k]));
//          cerr<<j<<" s="<<s[j]<<endl;
        }
        for(rg int j=1;j<i;++j)
            f[i]=add(f[i],mul(s[j],add(f[j],1)));
        f[i]=add(f[i],s[i]);
        f[i]=div(f[i],sub(fac[i],s[i]));
        rg int ans=0;
        for(rg int j=1;j<=i;++j)
            ans=add(ans,mul(s[j],f[j]));
        ans=mul(ans,ifac[i]);
        printf("%d,\n",ans);
    }
    return 0;
}

最后的代码就59KB的样子，可以接受，于是时间复杂度成功降为\(O(1)\)

标解

技术分享图片
技术分享图片

std有三份代码

第一份

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define FOR(i, l, r) for(int i = (l); i <= (r); i++)
#define REP(i, l, r) for(int i = (l); i != (r); i++)
#define DFR(i, l, r) for(int i = (l); i >= (r); i--)
#define DRP(i, l, r) for(int i = (l); i != (r); i--)

using namespace std;

#define DEBUG(arg...) fprintf(stderr, arg)

namespace FI {
    const int SIZE = 1 << 18 | 1;
    char buf[SIZE], *front, *back;

    void NextChar(char &c) {
        if(front == back) back = (front = buf) + fread(buf, 1, SIZE, stdin);
        c = (front == back) ? (char)EOF : *front++;
    }

    template<typename T> void NextNum(T & x) {
        char c; int f = 1;
        for(NextChar(c); c > '9' || c < '0'; NextChar(c)) if(c == '-') f = -1;
        for(x = 0; c >= '0' && c <= '9'; NextChar(c)) x = (x << 3) + (x << 1) + c - '0';
        x *= f;
    }
}

typedef long long LL;

const int maxn = 5000 + 47;
const int mod = 1e9 + 7;

int n, inv[maxn];
int f[maxn][maxn], g[maxn];

int fpow(int a, int b) {
    int res = 1;
    while(b) {
        if(b & 1) res = 1LL * res * a % mod;
        a = 1LL * a * a % mod;
        b >>= 1;
    }
    return res;
}

int main() {
    freopen("monkey.in", "r", stdin);
    freopen("monkey.out", "w", stdout);

    scanf("%d", &n);

    inv[1] = 1;
    for(int i = 2; i <= n; i++) inv[i] = 1LL * (mod - mod / i) * inv[mod % i] % mod;

    f[1][1] = 1;
    for(int i = 2; i <= n; i++)
        for(int j = 1; j <= i; j++)
            f[i][j] = (1LL * f[i - 1][j] * inv[i] % mod + 1LL * f[i - 1][j - 1] * (j - 1) % mod * inv[i] + (j >= 3 ? 1LL * f[i - 1][j - 2] * (i - j + 1) % mod * inv[i] : 0)) % mod;
    
    g[1] = 1;
    for(int i = 2; i <= n; i++) {
        g[i] = 1;
        for(int j = 2; j < i; j++)
            g[i] = (g[i] + 1LL * g[j] * f[i][j] % mod) % mod;
        g[i] = 1LL * g[i] * fpow(1 - f[i][i] + mod, mod - 2) % mod;
    }

    printf("%d\n", (g[n] - 1 + mod) % mod);
}

第二份

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define FOR(i, l, r) for(int i = (l); i <= (r); i++)
#define REP(i, l, r) for(int i = (l); i != (r); i++)
#define DFR(i, l, r) for(int i = (l); i >= (r); i--)
#define DRP(i, l, r) for(int i = (l); i != (r); i--)

using namespace std;

#define DEBUG(arg...) fprintf(stderr, arg)

namespace FI {
    const int SIZE = 1 << 18 | 1;
    char buf[SIZE], *front, *back;

    void NextChar(char &c) {
        if(front == back) back = (front = buf) + fread(buf, 1, SIZE, stdin);
        c = (front == back) ? (char)EOF : *front++;
    }

    template<typename T> void NextNum(T & x) {
        char c; int f = 1;
        for(NextChar(c); c > '9' || c < '0'; NextChar(c)) if(c == '-') f = -1;
        for(x = 0; c >= '0' && c <= '9'; NextChar(c)) x = (x << 3) + (x << 1) + c - '0';
        x *= f;
    }
}

typedef long long LL;

const int maxn = 5000 + 47;
const int mod = 1e9 + 7;

int n, inv[maxn];
int f[maxn][maxn], g[maxn];

int fpow(int a, int b) {
    int res = 1;
    while(b) {
        if(b & 1) res = 1LL * res * a % mod;
        a = 1LL * a * a % mod;
        b >>= 1;
    }
    return res;
}

int main() {
    freopen("monkey.in", "r", stdin);
    freopen("monkey.out", "w", stdout);

    scanf("%d", &n);

    inv[1] = 1;
    for(int i = 2; i <= n; i++) inv[i] = 1LL * (mod - mod / i) * inv[mod % i] % mod;

    f[1][1] = 1;
    for(int i = 2; i <= n; i++)
        for(int j = 1; j <= i; j++)
            f[i][j] = (1LL * f[i - 1][j] * inv[i] % mod + 1LL * f[i - 1][j - 1] * (j - 1) % mod * inv[i] + (j >= 3 ? 1LL * f[i - 1][j - 2] * (i - j + 1) % mod * inv[i] : 0)) % mod;
    
    g[1] = 0;
    for(int i = 2; i <= n; i++) {
        for(int j = 2; j < i; j++)
            g[i] = (g[i] + 1LL * (g[j] + 1) * f[i][j] % mod) % mod;
        g[i] = (g[i] + f[i][i]) % mod;
        g[i] = 1LL * g[i] * fpow(1 - f[i][i] + mod, mod - 2) % mod;
    }

    printf("%d\n", (g[n] + mod) % mod);
}

第三份

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define FOR(i, l, r) for(int i = (l); i <= (r); i++)
#define REP(i, l, r) for(int i = (l); i != (r); i++)
#define DFR(i, l, r) for(int i = (l); i >= (r); i--)
#define DRP(i, l, r) for(int i = (l); i != (r); i--)

using namespace std;

#define DEBUG(arg...) fprintf(stderr, arg)

namespace FI {
    const int SIZE = 1 << 18 | 1;
    char buf[SIZE], *front, *back;

    void NextChar(char &c) {
        if(front == back) back = (front = buf) + fread(buf, 1, SIZE, stdin);
        c = (front == back) ? (char)EOF : *front++;
    }

    template<typename T> void NextNum(T & x) {
        char c; int f = 1;
        for(NextChar(c); c > '9' || c < '0'; NextChar(c)) if(c == '-') f = -1;
        for(x = 0; c >= '0' && c <= '9'; NextChar(c)) x = (x << 3) + (x << 1) + c - '0';
        x *= f;
    }
}

typedef long long LL;

const int maxn = 5000 + 47;
const int mod = 1e9 + 7;

int n;
int f[maxn], g[maxn];
int h[maxn], s[maxn];
int l[maxn][maxn];

int fpow(int a, int b) {
    int res = 1;
    while(b) {
        if(b & 1) res = 1LL * res * a % mod;
        a = 1LL * a * a % mod;
        b >>= 1;
    }
    return res;
}

int C(int a, int b) {
    return (int)(1LL * f[a] * g[b] % mod * g[a - b] % mod);
}

int main() {
    freopen("monkey.in", "r", stdin);
    freopen("monkey.out", "w", stdout);

    scanf("%d", &n);

    f[1] = 1;
    for(int i = 2; i <= n; i++) f[i] = 1LL * f[i - 1] * i % mod;
    g[n] = fpow(f[n], mod - 2);
    for(int i = n - 1; i >= 0; i--) g[i] = 1LL * g[i + 1] * (i + 1) % mod;

    for(int i = 2; i <= n; i++) {
        for(int j = 0; j < i; j++) {
            h[i] = (h[i] + 1LL * C(i - 1, j) * f[i - j] % mod * ((j & 1) ? -1 : 1) % mod + mod) % mod;
        }
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            l[i][j] = 1LL * C(i - 1, j - 1) * h[j] % mod * g[i] % mod;
        }
    }
    s[1] = 0;
    for(int i = 2; i <= n; i++) {
        for(int j = 2; j < i; j++) s[i] = (s[i] + 1LL * (s[j] + 1) * l[i][j] % mod) % mod;
        s[i] = (s[i] + l[i][i]) % mod;
        s[i] = 1LL * s[i] * fpow(1 - l[i][i] + mod, mod - 2) % mod;
    }
    printf("%d\n", s[n]);
}

test20181107 猴子排序

标签：cstring   names   name   十分   mod   space   stdout   git   pow   

原文地址：https://www.cnblogs.com/autoint/p/9924532.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！