标签:无向图 using 卡尔 cout 包含 code find 集合 col
首先来看看什么是最小生成树。
在一个无向连通图中,如果存在一个连通子图包含原图中所有的结点和部分边,且这个子图不存在回路(不成环),那么我们称这个子图为原图的一棵生成树。在带权图中,所有的生成树中边权的和最小的那棵(或几棵)被称为最小生成树。
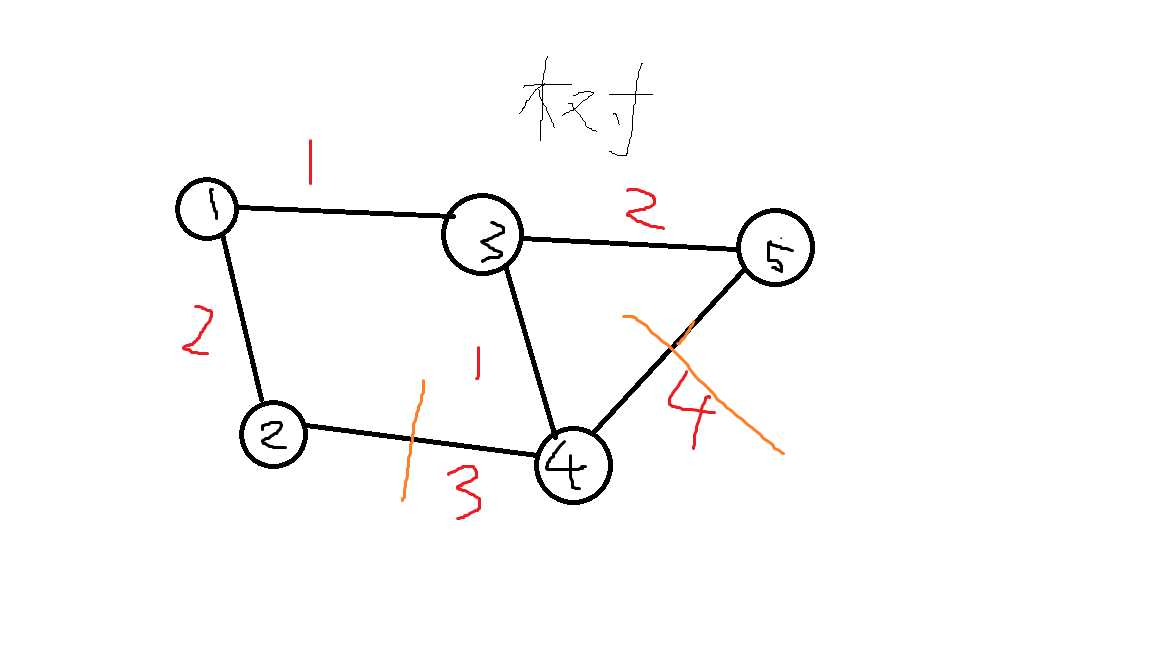
注:图为无向图,红字表示边的权值,橙线表示不取的边。
最终:最小生成树=1→2的权值+1→3的权值+3→4的权值+3→5的权值=2+1+1+2=6
克鲁斯卡尔是求最小生成树的算法之一,多用于稠密图。
进行以下步骤,直到取的边数等于点数减一。
(1)初始时所有结点属于孤立的集合。
(2)按照边权递增顺序遍历所有的边,若遍历到的边两个顶点仍分属不同的集合(该边即为联通这两个集合的边中权值最小的那条)则确定该边为最小生成树上的一条边,并将这两个顶点分属的集合合并。
(3)遍历完所有边后,原图上所有结点属于同一个集合则被选取的边和原图中所有结点构成最小生成树;否则原图不连通,最小生成树不存在。
上代码
#include<bits/stdc++.h>
using namespace std;
int n,parent[105]={-1};
struct edge //表示一条有向边
{
int b /*起点*/,e/*终点*/,v/*权值*/;
}a[5005];
void Initialize() //初始化,令每一个点的祖宗都为它自己。
{
for(int i=0;i<n;i++) parent[i]=i;
}
int findfather(int x) //寻找一个点的祖宗
{
if(x==parent[x]) return x;
else return parent[x]=findfather(parent[x]);
}
void Union(int x,int y) //并查集,把一个点的祖宗变成另一个点的祖宗。也就是将两个集合合并。
{
parent[findfather(x)]=findfather(y);
}
bool isfather(int x,int y) //判断两个点是否处于同一集合
{
return findfather(x)==findfather(y);
}
bool cmp(edge x,edge y)
{
return x.v<y.v;
}
int main()
{
int k=0;
cin>>n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
int cost;
cin>>cost;
if(i<j)
{
a[k].b=i;
a[k].e=j;
a[k].v=cost;
++k;
}
}
}
sort(a,a+k,cmp); //把所有边按从大到小排序
Initialize();
int cnt=0;
int i=0;
int sum=0;
while(cnt!=n-1)
{
edge tmp=a[i++];
if(!isfather(tmp.b,tmp.e)) //如果两点不处于同一集合,则加上这条边
{
sum+=tmp.v;
cnt++;
Union(tmp.b,tmp.e); //将两个集合合并
}
}
cout<<sum;
return 0;
}
/*
输入样例
3
0 1 2
1 0 1
2 1 0
输出样例
2
*/
标签:无向图 using 卡尔 cout 包含 code find 集合 col
原文地址:https://www.cnblogs.com/zxjhaha/p/11192947.html