TopCoder12584 SemiPerfectPower

标签：技术   就是   现在   continue   while   iperf   枚举   两种   vector   

首先我们可以把答案差分,那么我们只需要求出\(1\)~\(x\)范围内的满足条件的数即可.

题目要求的应该是这个东西的个数:

\(l \leq a*b^c \leq r(1 \le a < b)?\)的个数

我们首先对于问题仔细分析一波,发现\(c>3\)显然不需要考虑.

1. \(c>3\)且\(c\)是偶数.

显然\(a*b^{2k}=a*({b^k})^2\),显然如果\(a<b\)那么\(a<b^k(k>1)\)

1. \(c>3\)且\(c\)是奇数.

显然\(a*b^{2k+1}=(a*b)*({b^k})^2\),显然如果\(a<b\)那么\(a<b^{k-1}(k>1)\)

所以现在我们成功把题目转换成了两种情况:\(c=2\)|\(c=3\)

单独计算\(c=2\)和\(c=3\)都十分的简单,但是极其有可能有这样子的情况:

\(a*x^2=b*y^3\)

这个时候我们就需要排除这种情况.

不妨先把\(a*x^2\)算出来,那么只需要计算满足\(b*y^3\)且\(a \ge x\)

\(a*x^2\)显然只需要枚举\(i \in [1,\sqrt[3]{x}]\)然后就是\(\sqrt{x/i}-i\),因为要排除掉\(a \ge x\)的情况.

现在问题就在于如何统计\(b*y^3 \leq x\)且\(a*x^2(a \ge x)\)

我们推一波式子:

下面是手写稿,主要是不想写\(LaTeX\)了.

/*
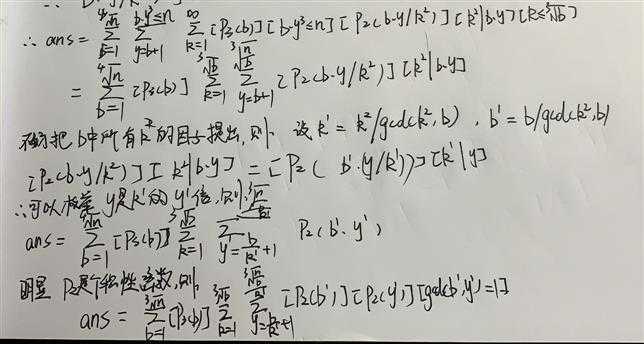
  mail: mleautomaton@foxmail.com
  author: MLEAutoMaton
  This Code is made by MLEAutoMaton
*/
#include<bits/stdc++.h>
using namespace std;
const int M=430890,N=16820;
class SemiPerfectPower{
public:
    vector<int>son[M],sum[N];
    int mu[M],thr_out[M];
    int pfg(long long x){
        int l=0,r=3e8,ret=0;
        while(l<=r){
            int mid=(l+r)>>1;
            if(1ll*mid*mid<=x){ret=mid;l=mid+1;}
            else r=mid-1;
        }
        return ret;
    }
    int lfg(long long x){
        int l=0,r=M,ret=0;
        while(l<=r){
            int mid=(l+r)>>1;
            if(1ll*mid*mid*mid<=x){ret=mid;l=mid+1;}
            else r=mid-1;
        }
        return ret;
    }
    long long solve(long long x){
        long long ans=0;
        for(int i=1;1ll*i*i*i<=x;i++)if(mu[i])ans+=pfg(x/i)-i;
        for(int i=1;1ll*i*i*i*i<=x;i++)
            if(!thr_out[i])
                for(int j=1;j*j*j<=i;j++){
                    int d=__gcd(j*j,i);
                    if(!mu[i/d])continue;
                    int k=j*j/d,l=i/k,r=lfg(x/i)/k;
                    for(int u:son[i/d])ans+=mu[u]*(sum[u][r/u]-sum[u][l/u]);
                }
        return ans;                            
    }
    long long count(long long l,long long r){
        mu[1]=1;
        for(int i=1;i<M;i++)if(mu[i])for(int j=i<<1;j<M;j+=i)mu[j]-=mu[i];
        for(int i=1;i<M;i++)if(mu[i])for(int j=i;j<M;j+=i)if(mu[j])son[j].push_back(i);
        for(int i=2;i*i*i<M;i++)for(int j=i*i*i;j<M;j+=i*i*i)thr_out[j]=1; 
        for(int i=1;i<N;i++){
            sum[i].resize(M/i+1);
            sum[i][0]=0;
            for(int j=1;j<M/i+1;j++)
                sum[i][j]=sum[i][j-1]+(mu[i*j]!=0);
        }
        return solve(r)-solve(l-1);
    }
};

TopCoder12584 SemiPerfectPower

标签：技术   就是   现在   continue   while   iperf   枚举   两种   vector   

原文地址：https://www.cnblogs.com/mle-world/p/11210704.html