标签:strong 一条直线 代码 NPU scanf sam using 直线 情况
给出一座山,如图。
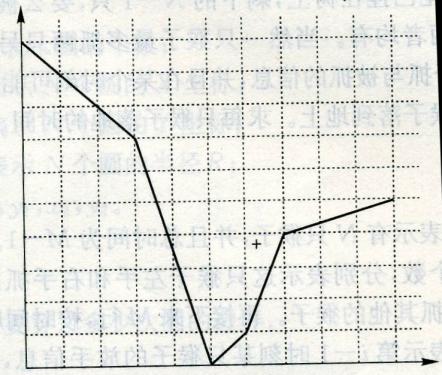
现在要在山上的某个部位装一盏灯,使得这座山的任何一个部位都能够被看到。
给出最小的y坐标,如图的+号处就是y坐标最小的安装灯的地方。
第一行一个数N,表示这座山由N个点构成;
接下来N行从左到右给出了这座山的构造情况,每行两个数Xi、Yi,表示一个折点,保证Xi>Xi-1
仅输出一行,为最小的y坐标,当你的答案与标准答案相差不超过0.01时,则被认为是正确的。
6 0 0 10 0 11 1 15 1 16 0 25 0
3.00
数据规模:
30%的数据,1≤N≤50;
100%的数据,1≤N≤5000;0≤Xi,Yi≤100000,保证答案不超过1000000.
如果我们把相邻的两个点连接起来,看作一条条直线,那么我们可以发现我们要求的就是找到一个点,使它在每一条的直线的上方或在直线上,并且要求y坐标越小越好。
首先第一步当然是这n-1条直线的表达式给求出来(见初二上册数学课本)
然后我们会发现,对于我们枚举的每一个高度,对于每一条直线都有一个满足要求的区间,那么我们怎么判断这个高度是否可行?显然,若这些区间有交集的话,那么就是有解了,否则就是不行。
枚举高度我们可以通过二分来实现,剩下就是解一下不等式问题就可以了。
代码
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=5010;
int n;
double l,r,mid;
double ll,rr,ans;
struct no {
int x,y;
} a[N];
struct nod {
double k,b;
} b[N];
bool check(double x) {
ll=-2e9,rr=2e9;
for(int i=1; i<n; i++) {
if(b[i].k<0)
ll=max(ll,(x-b[i].b)/b[i].k);
if(b[i].k>0)
rr=min(rr,(x-b[i].b)/b[i].k);
if (b[i].k==0&&b[i].b>x)
return 0;
}
return ll<=rr;
}
int main () {
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%d%d",&a[i].x,&a[i].y);
for(int i=1; i<n; i++) {
b[i].k=1.0*(a[i].y-a[i+1].y)/(a[i].x-a[i+1].x);
b[i].b=1.0*a[i].y-b[i].k*a[i].x;
}
l=0,r=1000000;
ans=-1;
while(r-l>=0.001) {
mid=(l+r)/2;
if(check(mid)) {
ans=mid;
r=mid;
} else
l=mid;
}
printf("%.2lf\n",ans);
return 0;
}
标签:strong 一条直线 代码 NPU scanf sam using 直线 情况
原文地址:https://www.cnblogs.com/mysh/p/11581807.html