标签：hdu

http://acm.hdu.edu.cn/showproblem.php?pid=5073

Galaxy

Good news for us: to release the financial pressure, the government started selling galaxies and we can buy them from now on! The first one who bought a galaxy was Tianming Yun and he gave it to Xin Cheng as a present.


To be fashionable, DRD also bought himself a galaxy. He named it Rho Galaxy. There are n stars in Rho Galaxy, and they have the same weight, namely one unit weight, and a negligible volume. They initially lie in a line rotating around their center of mass.

Everything runs well except one thing. DRD thinks that the galaxy rotates too slow. As we know, to increase the angular speed with the same angular momentum, we have to decrease the moment of inertia.

The moment of inertia I of a set of n stars can be calculated with the formula


where w_i is the weight of star i, d_i is the distance form star i to the mass of center.

As DRD’s friend, ATM, who bought M78 Galaxy, wants to help him. ATM creates some black holes and white holes so that he can transport stars in a negligible time. After transportation, the n stars will also rotate around their new center of mass. Due to financial pressure, ATM can only transport at most k stars. Since volumes of the stars are negligible, two or more stars can be transported to the same position.

Now, you are supposed to calculate the minimum moment of inertia after transportation.

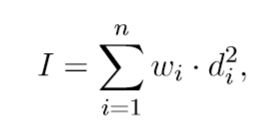
2
3 2
-1 0 1
4 2
-2 -1 1 2

0
0.5

题意：数轴上n个点，可以任意移动k个点，要使得移动后的数的方差最小，问最小的值是多少。

分析：首先可以想到要移动的点肯定是两端的某些点，也就是剩下的点是连续的，而且移动后的位置肯定是剩下的点平均位置的地方。这样其实我们就枚举连续的n-k个数的起点，求这些数的方差即可。

如果是n^2去求肯定会超时，这里注意到(xi-x‘)^2=xi^2+x‘^2-2*x*x‘(x‘是平均数)，我们就维护一个连续n-k个数的平方和以及和,到下一个点时类似滑动窗口一加一减就可以算出此时的平方和以及和。那么最后的方差就等于sum(x^2)+(sum(x)/m)^2*m-2*sum(x)*sum(x)/m

化简下就是sum(x^2)-sum(x)*sum(x)/m。注意特判n-k为0的情况。

/**
 * @author neko01
 */
//#pragma comment(linker, "/STACK:102400000,102400000")
#include <cstdio>
#include <cstring>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
#include <cmath>
#include <set>
#include <map>
using namespace std;
typedef long long LL;
#define min3(a,b,c) min(a,min(b,c))
#define max3(a,b,c) max(a,max(b,c))
#define pb push_back
#define mp(a,b) make_pair(a,b)
#define clr(a) memset(a,0,sizeof a)
#define clr1(a) memset(a,-1,sizeof a)
#define dbg(a) printf("%d\n",a)
typedef pair<int,int> pp;
const double eps=1e-9;
const double pi=acos(-1.0);
const int INF=0x3f3f3f3f;
const LL inf=(((LL)1)<<61)+5;
const int N=50005;
double a[N];
int main()
{
    int n,k,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++)
        {
            scanf("%lf",&a[i]);
        }
        sort(a+1,a+1+n);
        int m=n-k;
        if(m==0)
        {
            puts("0");
            continue;
        }
        double ans,ave,s1=0,s2=0;
        for(int i=1;i<=m;i++)
        {
            s2+=a[i];
            s1+=a[i]*a[i];
        }
        ans=s1-s2*s2/m;
        for(int i=1;i<=k;i++)
        {
            s1=s1-a[i]*a[i]+a[i+m]*a[i+m];
            s2=s2-a[i]+a[i+m];
            ans=min(ans,s1-s2*s2/m);
        }
        printf("%.9f\n",ans);
    }
    return 0;
}

hdu5073 2014鞍山现场赛D题

标签：hdu

原文地址：http://blog.csdn.net/neko01/article/details/40518877