标签:bsp class mic 转化 ret 存储 位置 坑点 介绍



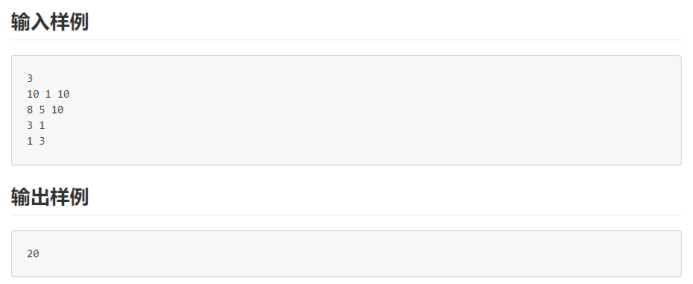
最基础的流水线调度问题,甚至没有开始和结束的值
知识点:动态规划,流水线调度
实现方法即得出状态转移方程后完善即可,设a[][i]存储着第一二条线上各家的时间花费,t[][i]存储着i处进行线路切换的花费,f[][i]存储着各线在i处的最小花费。
则对每一个f[][i]应有如下的转移方程:
f[0][1] = a[0][1];
f[1][1] = a[1][1];
f[0][i] = min(f[0][i-1]+a[0][i],f[1][i-1]+t[1][i-1]+a[0][i]);
f[1][i] = min(f[1][i-1]+a[1][i],f[0][i-1]+t[0][i-1]+a[1][i]);
前两个为初始定义,后两个为具体的转换。
min函数中前一个值表示直接在当前这条线的前一个结点前进的花费,后一个表示从另一条线的前一个结点先转移过来后再前进的花费。此时只有两条线因此只有这两种情况,所以比较后便可得出到达该线该位置的最小花费。
多条线的情况可参考:题解:说好的ALS呢?(后续添加链接)
最后比较到达n处(最后一个家)哪条线的时间花费最小即可。
坑点:
注意多次输入后数组的初始化,以及状态转移方程的正确转化即可
完整代码:
//流水线调度基本问题
#include<iostream>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
int n;
int fend;
int i;
while(cin >> n)
{
int a[2][n+1],t[2][n];
//两条线上每一家花费的时间
for(i = 1;i<=n;i++)
cin >> a[0][i];
for(i = 1;i<=n;i++)
cin >> a[1][i];
//两条线不同位置转移的时间花费
for(i = 1;i<n;i++)
cin >> t[0][i];
for(i = 1;i<n;i++)
cin >> t[1][i];
//存储两条线不同位置的最小时间
int f[2][n+1];
//初始化防止错误
f[0][1] = a[0][1];
f[1][1] = a[1][1];
for(i = 2;i<=n;i++)
{
//具体状态转移方程介绍见实现解释
if(f[0][i-1]+a[0][i]<f[1][i-1]+t[1][i-1]+a[0][i])
f[0][i] = f[0][i-1]+a[0][i];
else
f[0][i] = f[1][i-1]+t[1][i-1]+a[0][i];
if(f[1][i-1]+a[1][i]<f[0][i-1]+t[0][i-1]+a[1][i])
f[1][i] = f[1][i-1]+a[1][i];
else
f[1][i] = f[0][i-1]+t[0][i-1]+a[1][i];
}
//计算两条线分别的最后时间花费得最小值
if(f[0][n]<f[1][n])
fend = f[0][n];
else
fend = f[1][n];
cout << fend << ‘\n‘;
}
return 0;
}
标签:bsp class mic 转化 ret 存储 位置 坑点 介绍
原文地址:https://www.cnblogs.com/doUlikewyx/p/11700784.html