标签:src 维护 div red 一个 ase 旋转 key 目的
一颗红黑树是满足下面红黑性质的二叉搜索树
①每个结点或是红的,或是黑的。
②根结点是黑的
③每个叶结点(NIL)是黑的
④如果一个结点是红色的,则它的两个子结点是黑色的。
⑤对每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
插入时总是要考虑它的叔叔,删除时总要考虑它的兄弟。而且插入时维护的主要是颜色(性质4),而删除时维护的主要是黑色结点数量(性质5)
旋转

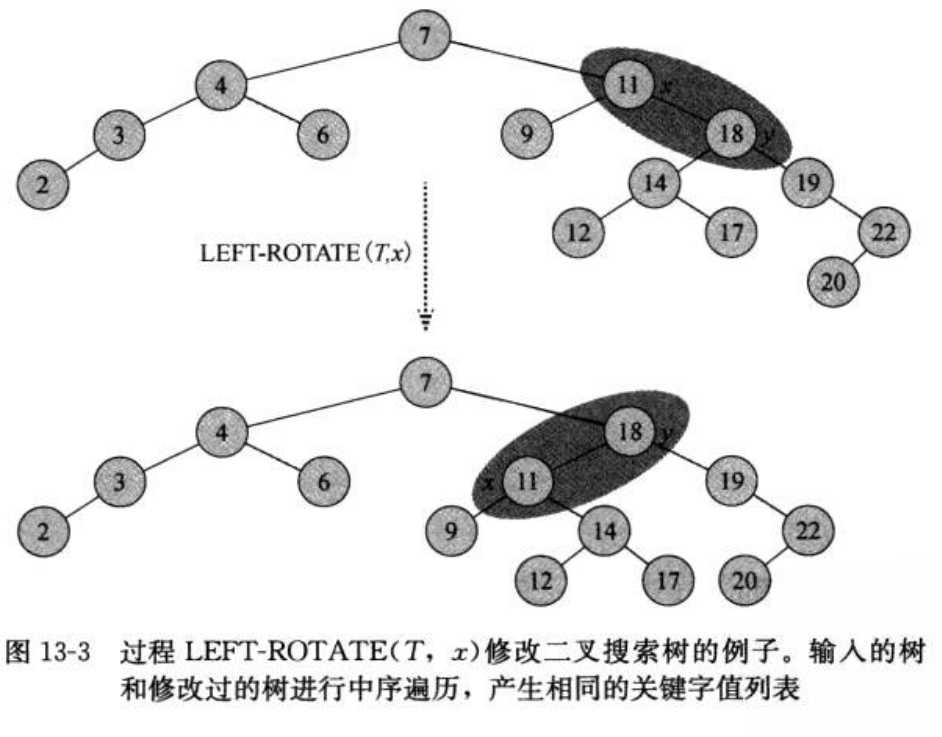
void left_rotate(ROOT &T, RBTREE x)
{
RBTREE y;
y = x->left;
x->right = y->left;
if (y->left != T->nil)
y->left->p = x;
y->p= x->p;
if (x->p == T->nil)
T->root = y;
else if (x->p->left == x)
x->p->left = y;
else x->p->right = y;
y->left = x;
x->p = y;
}
void right_rotate(ROOT &T,RBTREE y)
{
RBTREE x;
x = y->right;
y->left = x->right;
if (x->right == T->nil)
x->right->p = y;
x->p = y->p;
if (y->p == T->nil)
T->root = x;
else if (y->p->left = y)
y->p->left = x;
else
y->p->right = x;
x->right = y;
y->p = x;
}
插入
void rb_insert(ROOT &T, RBTREE z)
{
RBTREE x, y;
y = T->nil;
x = T->root;
while (x != T->nil)
{
y = x;
if (z->key < x->key)
x = x->left;
else
x = x->right;
}
z->p = y;
if (y == T->nil)
T->root = z;
else if (z->key < y->key)
y->left = z;
else
y->right = z;
z->left = T->nil;
z->right = T->nil;
z->color = RED;
rb_insert_fixup(T, z);
}
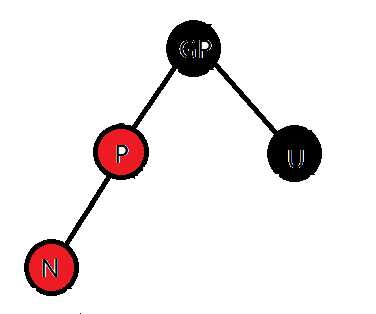
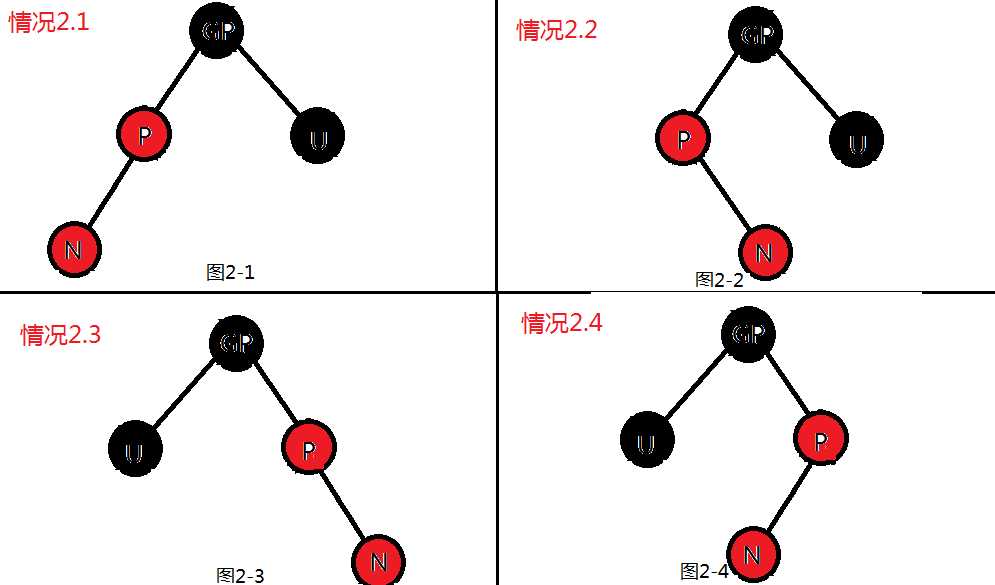
void rb_insert_fixup(ROOT &T, RBTREE z)
{
RBTREE y;
while (z->p->color == RED)
{
if (z->p == z->p->p->left)
{
y = z->p->p->right;
if (y->color == RED) //case1.1
{
z->p->color = BLACK;
z->p->p->color = RED;
y->color = BLACK;
z = z->p->p;
}
else if (z == z->p->right) //case2中的case2.2
{
z = z->p;
left_rotate(T, z);
}
z->p->color = BLACK; //case2.1
z->p->color = RED;
right_rotate(T, z->p->p);
}
else//(z->p == z->p->p->right)
{
y = z->p->p->left;
if (y->color == RED) //case1.2
{
z->p->color = BLACK;
z->p->p->color = RED;
y->color = BLACK;
z = z->p->p;
}
else if (z = z->p->left) //case2中的2.4
{
z = z->p;
right_rotate(T, z);
}
z->p->color = BLACK; //case2.3
z->p->color = RED;
left_rotate(T, z->p->p);
}
}
}
标签:src 维护 div red 一个 ase 旋转 key 目的
原文地址:https://www.cnblogs.com/KIROsola/p/12238618.html