标签:旋转 line 就是 信息 mit 欧氏距离 归一化 相互 central
一元高斯分布:
\[
N(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})
\]
对于D维向量\(\boldsymbol x\),多元高斯分布为:
\[
N(\boldsymbol{x}|\boldsymbol{\mu},\boldsymbol{\Sigma})=\frac{1}{(2\pi)^{\frac{D}{2}}|\boldsymbol\Sigma|^{\frac{1}{2}}}\exp(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}))
\]
其中,\(\Sigma\)为\(D \times D\)维协方差矩阵,\(|\Sigma|\)为其行列式,\(\boldsymbol \mu\)为D维的均值向量。
使熵取得最大值的分布为高斯分布,原因在这里:最大熵与正态分布。
并且根据拉普拉斯提出的中心极限定理(central limit theorem),对于某些温和的情况,一组随机变量之和的概率分布在项的数量增加时逐渐趋于高斯分布。比如说多个均匀分布相加,在其数量趋向正无穷时,和的分布趋向高斯分布。
高斯分布对于\(\boldsymbol{x}\)的依赖是通过下面的二次型:
\[
\triangle^2=(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})
\]
这个二次型出现在指数的位置上。\(\triangle\)为\(\boldsymbol{x},\boldsymbol{\mu}\)两者之间的马氏距离。当\(\Sigma\)是单位矩阵时,变成了欧式距离。
取\(\boldsymbol\Sigma\)为对称矩阵,使其特征值是正交的。(书上说取对称矩阵不失一般性,因为任何非对称项都会从指数中消失,这个我不太明白,可能与矩阵指数有关)
现在考虑协方差矩阵的特征值(令\(\boldsymbol A = \boldsymbol\Sigma\)):
\[
\boldsymbol A\boldsymbol{u}_i=\lambda_i\boldsymbol{u}_i
\]
对于不同的特征值\(\lambda_i\),\(\lambda_j\),其对应的特征向量必为正交的,即:
\[
\boldsymbol{u}_i^T\boldsymbol{u}_j=I_{ij}
\]
其中\(I_{ij}\)表示单位矩阵的一个元素。
由于\(\boldsymbol A\)为n阶正定矩阵,\(r(\boldsymbol A)=n\),对于n阶实对称矩阵,一定可以对角化,那么一定有n个线性无关的特征向量。那么可以对其进行特征分解。
设对角矩阵\(\boldsymbol\Lambda\),正交矩阵\(\boldsymbol U\)(进行了特征分解):
\[
\boldsymbol\Lambda =
\begin{pmatrix}
\lambda_1& &\&\lambda_2&\&&\lambda_D
\end{pmatrix},\ \ \boldsymbol U =
\begin{pmatrix}
\boldsymbol u_1,\boldsymbol u_2...\boldsymbol u_D
\end{pmatrix}
\]
则:
\[
\boldsymbol A=\boldsymbol U\boldsymbol \Lambda\boldsymbol U^T=\sum_i^D\lambda_i\boldsymbol u_i\boldsymbol u_i^T \nonumber \\boldsymbol A^{-1}=\sum_i^D\frac{1}{\lambda_i}\boldsymbol u_i\boldsymbol u_i^T \nonumber, \ \ (\boldsymbol u_i^T=\boldsymbol u_i^{-1})
\]
此时二次型变为:
\[
\triangle^2 =\sum_i^D \frac{\boldsymbol y_i^2}{\lambda_i}
\]
其中,\(y_i=\boldsymbol u_i^T(\boldsymbol{x}-\boldsymbol{\mu})\),可以理解\(y_i\)是正交向量\(\boldsymbol u_i\)关于原始坐标\(x_i\)坐标经过平移和旋转之后形成的新的坐标系。
定义\(\boldsymbol y = (y_1,...,y_D)^T\),就有:
\[
\boldsymbol y = \boldsymbol U^T(\boldsymbol{x}-\boldsymbol{\mu})
\]
\(\boldsymbol y = (y_1,...,y_D)^T\),\(y_1\)表示在该方向上的坐标。
\(\boldsymbol x = (x_1,...,x_D)^T\),\(x_1\)表示在该方向上的坐标。两者的不同在于\(y\)坐标系是\(x\)坐标系经过平移旋转后得到的。
\(\boldsymbol U = (\boldsymbol u_1, ... ,\boldsymbol u_D)\),\(\boldsymbol u_1=(u_{11}, ... ,u_{1D})^T\),表示特征向量组成的矩阵。
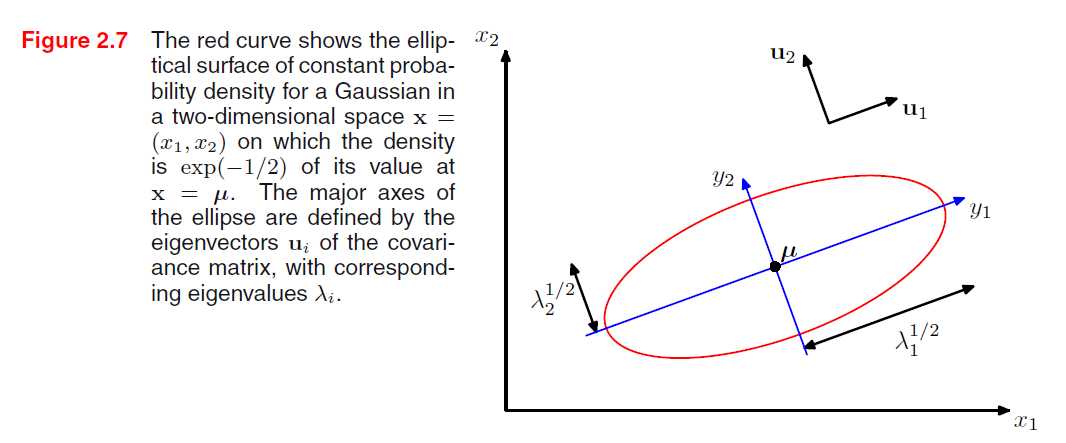
这个图是PRML书中的图2.7,关于其理解写在这里。表示在高斯密度为常数时的曲面,为椭球面。其中心为\(\boldsymbol \mu\),轴的方向为\(\boldsymbol u_1,\boldsymbol u_2\),放缩因子为\(\sqrt\lambda\)。
我们有必要限制协方差矩阵的所有特征值严格大于0,否则分布不能被正确的归一化。此时该矩阵成为正定矩阵(positive definite matrix)。
下面考虑在\(\boldsymbol y\)坐标系下的高斯分布的形式。我们有一个雅各比矩阵(Jacobian),其元素为:
\[
J_{ij}=\frac{\part x_i}{\part y_j}=U_{ij}
\]
如何得出的呢?根据上面公式:
\[
\begin{align}
\boldsymbol U^T(\boldsymbol{x}-\boldsymbol{\mu})\nonumber &= \boldsymbol y\\boldsymbol{x}-\boldsymbol{\mu} &= (\boldsymbol U^T)^{-1}\boldsymbol y\nonumber \\boldsymbol{x}-\boldsymbol{\mu} &= \boldsymbol U\boldsymbol y,\ \ 由于\boldsymbol U^T为正交矩阵\nonumber \x_1&= u_{11}y_1+u_{21}y_2+...+u_{D1}y_D
\end{align}
\]
可以看出\(\frac{\part x_1}{\part y_2}=u_{21}\),\(u_{21}\)表示特征向量\(\boldsymbol u_2\)的第一个值,在矩阵\(\boldsymbol U\)中为第一行第二列的元素,也就是\(U_{ij}=U_{12}\)。这就解释了雅各比矩阵的来源。再重复一遍,核心思想是矩阵\(\boldsymbol U\)是一个变换矩阵,包含着平移和选择的信息。
根据正交矩阵的性质,可以有:
\[
|\boldsymbol J|^2 = |\boldsymbol U|^2=|\boldsymbol U^T||\boldsymbol U|=|\boldsymbol U^T \boldsymbol U|=|\boldsymbol I|=1
\]
因此\(|\boldsymbol J|=1\),实际上由于这里只考虑其为正交矩阵,结果应为\(\pm 1\)。
之前的协方差矩阵的行列式可以写成:
\[
|\boldsymbol \Sigma|=\prod_{j=1}^D \lambda_j \nonumber \|\boldsymbol \Sigma|^{1/2}=\prod_{j=1}^D \lambda_j^{1/2} \nonumber
\]
回顾一下,在原坐标系\(\boldsymbol x\)下,高斯分布的形式为:
\[
p(\boldsymbol{x})=N(\boldsymbol{x}|\boldsymbol{\mu},\boldsymbol{\Sigma})=\frac{1}{(2\pi)^{\frac{D}{2}}|\boldsymbol\Sigma|^{\frac{1}{2}}}\exp(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu}))
\]
在经过上述推算后,在新坐标系\(\boldsymbol y\)下的高斯分布形式为:
\[
p(\boldsymbol{y})=p(\boldsymbol{x})|\boldsymbol{J}|=\prod_{j=1}^D\frac{1}{\sqrt{2\pi\lambda_j}}exp\left(-\frac{y_j^2}{2\lambda_j}\right)
\]
\(p(\boldsymbol{y})=p(\boldsymbol{x})|\boldsymbol{J}|\)之所以可以这么写,是因为雅各比矩阵就是特征矩阵,包含了平移和旋转的信息。
可以看到这其实就是D个独立一元高斯分布的乘积。就是说在特征向量定义的新的坐标系中,多元高斯分布可以理解为多个一维高斯分布的乘积。
其中:
\[
E(\boldsymbol{x})=\boldsymbol{\mu}\nonumber\Var(\boldsymbol{x})=\boldsymbol{\Sigma}
\]
高斯分布被广泛应用于概率密度模型,但是也有局限性。
协方差矩阵\(\boldsymbol{\Sigma}\)中有\(D(D+1)/2\)个参数,均值\(\boldsymbol{\mu}\)中也有\(D\)个参数。可以看到参数的增长速度是维度\(D\)的平方。
随着维度增加,矩阵的计算、求逆等等会变得无法计算。
有时候我们可以约束协方差矩阵为对角矩阵,即各个变量之间相互独立。这样却限制了其描述模型的能力。
高斯分布本质是单峰的,即只有一个最大值,这使得它不能近似多峰分布。
标签:旋转 line 就是 信息 mit 欧氏距离 归一化 相互 central
原文地址:https://www.cnblogs.com/LvBaiYang/p/12318152.html