标签:时间复杂度 求值 span 定义 个数 简单 中间 ref cout
其实这道题的关键就是在于预处理,其方法类似于 合唱队形
要想求出双子序列最大和,首先我们要会求出最大子段和
最大子段和的求值方法很简单
定义 \(f_i\) 为以第 \(i\) 个数结尾的最大子段和
#include <bits/stdc++.h>
using namespace std;
int f[1000010],a[1000010];
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
f[1]=a[1];
for(int i=2;i<=n;i++)f[i]=max(f[i-1]+a[i],a[i]);
int ans=f[1];
for(int i=2;i<=n;i++)ans=max(ans,f[i]);
cout<<ans;
return 0;
}那么我们现在可以去求双子序列最大和
怎么求,思路是
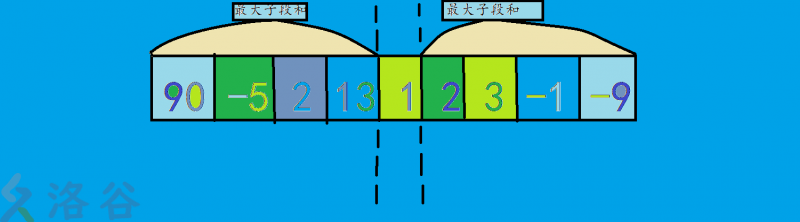
如果你去枚举中间的数,然后去算左边的最大子段,再算出右边的最大子段,加起来,用打擂法,求出最大值,你会 \(TLE\),毕竟\(n<=10^{6}\)
那怎么办?我们可以预处理
我们可以用 \(O(n)\) 的时间计算到前 \(1\) 个数的最大子段,
我们可以用 \(O(n)\) 的时间计算到后 \(i\) 个数的最大子段
像这样
cin>>n;
for(int i=1;i<=n;i++)cin>>x[i];
f[1]=x[1];
for(int i=2;i<=n;i++)f[i]=max(f[i-1]+x[i],x[i]);//算最大子段
for(int i=2;i<=n;i++)f[i]=max(f[i-1],f[i]);//更新成最大值
l[n]=x[n];
for(int i=n-1;i>=1;i--)l[i]=max(l[i+1]+x[i],x[i]);//算最大子段
for(int i=n-1;i>=1;i--)l[i]=max(l[i+1],l[i]);//更新成最大值这里 \(f_i\) 表示前 \(i\) 个数中的最大字段和
这里 \(l_i\) 表示后 \(i\) 个数中的最大字段和
然后,用 \(O(n)\) 的时间去枚举中间的数,打擂法求出双子序列最大和
上代码:
#include<bits/stdc++.h>
using namespace std;
long long x[1000010],f[1000010],l[1000010];
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++)cin>>x[i];
f[1]=x[1];
for(int i=2;i<=n;i++)f[i]=max(f[i-1]+x[i],x[i]);//算最大子段
for(int i=2;i<=n;i++)f[i]=max(f[i-1],f[i]);//算最大子段
l[n]=x[n];
for(int i=n-1;i>=1;i--)l[i]=max(l[i+1]+x[i],x[i]);//算最大子段
for(int i=n-1;i>=1;i--)l[i]=max(l[i+1],l[i]);//算最大子段
long long ans=f[1]+l[3];
for(int i=3;i<n;i++)ans=max(ans,f[i-1]+l[i+1]);//枚举中间数
cout<<ans;
return 0;
}这种预处理的方法可以优化我们的时间复杂度,避免重复计算,使我们的程序跑得更快!
标签:时间复杂度 求值 span 定义 个数 简单 中间 ref cout
原文地址:https://www.cnblogs.com/zhaohaikun/p/12326671.html