标签:follow 后序 bin 序列 figure 观察 技术 you fine
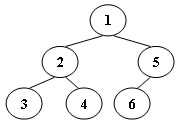
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop3 4 2 6 5 1通过观察Push和Pop的顺序可以发现,Push的顺序和先序遍历一样,Pop的顺序和中序遍历一样。因此可以先通过两个数组分别存储先序遍历序列和中序遍历序列,再通过这两个数组构建二叉树,最后再后序遍历即可。
#include <stdio.h>
#include <string.h>
#define MAXSIZE 30
struct StackNode {
int data;
struct StackNode *next;
};
typedef struct StackNode *Stack;
Stack createStack() {
Stack stack = (Stack) malloc(sizeof(struct StackNode));
stack->next = NULL;
return stack;
}
void push(Stack stack, int data) {
Stack node = createStack();
node->data = data;
node->next = stack->next;
stack->next = node;
}
int pop(Stack stack) {
if (!stack->next) return -1;
Stack top = stack->next;
int data = top->data;
stack->next = top->next;
free(top);
return data;
}
struct TreeNode {
int data;
struct TreeNode *left;
struct TreeNode *right;
};
typedef struct TreeNode *Tree;
int n, num = 0;
int preOrder[MAXSIZE], inOrder[MAXSIZE];
Tree createTree(int preL, int preR, int inL, int inR) {
if (preL > preR) return NULL;
Tree root = (Tree) malloc(sizeof(struct TreeNode));
root->data = preOrder[preL];
int rootIndex = inL;
for ( ; rootIndex <= inR; rootIndex++) {
if (preOrder[preL] == inOrder[rootIndex]) break;
}
int leftNums = rootIndex - inL;
root->left = createTree(preL + 1, preL + leftNums, inL, rootIndex - 1);
root->right = createTree(preL + leftNums + 1, preR, rootIndex + 1, inR);
return root;
}
void postOrder(Tree root) {
if (root == NULL) return;
postOrder(root->left);
postOrder(root->right);
printf("%d", root->data);
num++;
if (num < n) printf(" ");
}
int main() {
scanf("%d\n", &n);
Stack stack = createStack();
char input[5];
int data, preIndex = 0, inIndex = 0;
for (int i = 0; i < 2 * n; i++) {
scanf("%s", input);
if (strcmp(input, "Push") == 0) {
scanf("%d\n", &data);
push(stack, data);
preOrder[preIndex++] = data;
} else {
inOrder[inIndex++] = pop(stack);
}
}
Tree root = createTree(0, n - 1, 0, n - 1);
postOrder(root);
return 0;
}03-树3 Tree Traversals Again (25分)
标签:follow 后序 bin 序列 figure 观察 技术 you fine
原文地址:https://www.cnblogs.com/AndyHY-Notes/p/12540311.html