标签:vector 宽度 简单 多少 难度 地方 img 无法 bool
搬运老博文,因为最近又要用到网络流了。
网络流是一类图论算法,同时也多用于解决应用问题,是图论转化解决问题的代表性算法。
网络流(network-flows)是一种类比水流的解决问题方法,与线性规划密切相关。网络流的理论和应用在不断发展,出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。 ——百度百科
网络流图是一个有向图,不一定是有向无环图(DAG)。其中的点是网络流节点,边权是流量。大部分网络流有源点(S)和汇点(T)。如下:
如果把网络流图比作水管道系统,那么网络流节点就是一个水库,网络流边就是管道,网络流边的边权就是管道的宽度。源点就是某个输水的大江大河,汇点就是水最终流到的地方。
如果把网络流图比作电路图,那么源点汇点就分别是电源两头,网络流边就是导线,边权就是电流。
即源点到汇点的最大总流量。如果把网络流图比作水管道系统,那么就是求单位时间内源点到汇点能流多少水。概念较抽象,那么拿前面那张网络流图举例:
\(s\xRightarrow{flow=3} 1\)
\(s\xRightarrow{flow=1} 3\)
\(1\xRightarrow{flow=1} 2\)
\(3\xRightarrow{flow=2} 4\)
\(1\xRightarrow{flow=2} 4\)
\(2\xRightarrow{flow=2} t\)
\(4\xRightarrow{flow=2} t\)
结论:最大流为 \(3\)。
首先 \(s\) 处可以流出无限流量,但因为 \(s\) 到 \(1\) 的边流量只有 \(3\),所以 \(s\) 先向 \(1\) 流 \(3\) 的流量,现在 \(1\) 处有 \(3\) 的流量。因为是单位时间内的流量,所以 \(s\to1\) 的边就不能再用了。
同理,\(1\) 处的 \(3\) 份流量分到 \(2\) 和 \(4\) 处。\(1\to2\) 和 \(1\to4\) 的边不能再用。\(2\) 处有 \(1\) 流量,\(4\) 处有 \(2\) 流量。然后再通过边 \(2\to t\) 和 \(4\to t\) 向汇点 \(t\) 流 \(3\) 的流量。
然后再用 \(s\to3\),于是 \(3\) 处有了 \(1\) 的流量。然后再走 \(3\to 4\),因为 \(3\) 处只有 \(1\) 的流量,所以虽然 \(3\to4\) 能流 \(2\) 的流量,\(4\) 也只能得到 \(1\) 的流量。 然后再看 \(4\to t\) ,因为 \(4\to t\) 的边已经用完,所以即使 \(4\) 处有 \(1\) 的流量,\(t\) 也得不到一点流量。
所以最终最大流为 \(3\)。
不过现在先不讲最大流算法,过会儿你就知道为什么了。
定义
给定一个网络流图 \(G=(V,E)\),源点为 \(s\),汇点为 \(t\)。若一个边集 \(E‘?E\) 被删去后,\(s\) 和 \(t\) 不再联通,则称该边集为网络的割。边流量之和的最小的割称为网络的最小割。
再回到刚刚那个网络流图:
结论:最小割为 \(3\)。
先割断 \(1\to2\),再割断 \(4\to t\),\(s\) 和 \(t\) 不再联通。并且保证没有别的割法比这样更优。所以该网络流图的最小割为 \(3\) 。
蒟蒻的粗略证明:最大流必然有一些流满的边,如果把它们删掉,就是最小割了。如果删掉后还未成功割图,说明有些支流未流满,就不是最大流了。
通过上文我们已知一个网络流图的最小割等于它的最大流,所以求最大流的算法同样也是求最小割的算法。求最大流的算法很多,其中 \(Dinic\) 最为普遍使用。
\(Dinic\) 算法会对网络流图做一个分层。其实也就是做一次 \(Bfs\),把源点设为第 \(0\) 层,然后遍历源点的相邻节点,设为第 \(1\) 层,再遍历这些节点的相邻节点……直到汇点。
实现:
1.将源点的层次设为 \(0\),把源点设为已经访问,别的点设为未访问。
2.按照 \(Bfs\) 序遍历网络流图,为节点分层,遍历到终点结束。
3.在层次网络中,沿着相邻层 \(Dfs\) 搜索所有的增广路,并做相应的流量调整。
4.重复 \(1\sim 3\)。
算法较抽象,拿图举例(节点上的数为层次):
第一次建立层次网络,找到了蓝线表示的三条增广路,做流量调整。
第二次建立层次网络,上次流光的边这次不发挥作用,找到一条增广路。
第三次建立层次网络,汇点已经不能通过有用的边联通,算法终止。
如果你懂了,蒟蒻就放代码了。\(Dinic\) 最大流最小割算法:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
template<int V,int M>
class Dinic{
public:int E,g[V],to[M],nex[M],fw[M];
void clear(){memset(g,0,sizeof g),E=1;}
//E=1保证了互为反边的两条边可以通过^1互相得到
Dinic(){clear();}
//初始化
void add(int x,int y,int f){nex[++E]=g[x],to[E]=y,fw[E]=f,g[x]=E;}
//标准加边
void Add(int x,int y,int f){add(x,y,f),add(y,x,0);}
//加正边和反边,使得增广可以反悔
int dep[V],cur[V];bool vis[V];queue<int> q;
//dep表示层次,cur为单前弧优化,下面会讲。
//vis表示是否访问,queue维护bfs
bool bfs(int s,int t,int p){
for(int i=1;i<=p;i++) vis[i]=0,cur[i]=g[i];
q.push(s),vis[s]=1,dep[s]=0; //从源点开始bfs
while(q.size()){
int x=q.front();q.pop();
for(int i=g[x];i;i=nex[i])if(!vis[to[i]]&&fw[i])
q.push(to[i]),vis[to[i]]=1,dep[to[i]]=dep[x]+1;
//bfs过程中顺便给每个节点标上层次。
}
return vis[t]; //表示联通
}
int dfs(int x,int t,int F){
if(x==t||!F) return F;
int f,flow=0;
for(int&i=cur[x];i;i=nex[i]) //即i=g[x]
if(dep[to[i]]==dep[x]+1&&(f=dfs(to[i],t,min(F,fw[i])))>0) //沿着层次增广
{fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F) break;}
//边的流量调整
return flow; //一次增广的流量。
}
int dinic(int s,int t,int p){ //多次增广函数
int res=0,f;
while(bfs(s,t,p)) while((f=dfs(s,t,inf))) res+=f;
return res;
}
};
int n,m,s,t,p;
Dinic<10010,200010> net;
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t),p=n;
for(int i=1,x,y,f;i<=m;i++){
scanf("%d%d%d",&x,&y,&f);
net.Add(x,y,f);
}
printf("%d\n",net.dinic(s,t,p));
return 0;
}
以上代码读者可能有两个地方不懂:
1.反向反悔边
因为一条边的流量是通过以下代码调整的:
fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F) break;所以可以把反悔看成走反边,以得到最大流。
2.单前弧优化
for(int i=1;i<=p;i++) vis[i]=0,cur[i]=g[i];for(int&i=cur[x];i;i=nex[i])因为 \(Dinic\) 的增广是沿着加边顺序(严谨地说,是沿着加边反顺序)增广的,所以每一次增广时,前面几条边可能已经增广完了,这时,如果记录第一条没增广完的边,下一次增广从这条边开始,就方便、快很多。
\(EK\) 的全称叫 \(Edmonds-Karp\)。是一个与 \(Dinic\) 相比代码较短,跑得较慢的算法。
\(EK\) 就是简单地暴力搜索整个网络流图。在每次搜索增广路的时候,都采取 \(Bfs\) 的策略,将所有的从源点到汇点的路径都找出来,那么如果有增广路,就一定可以将它找出来。因此采用 \(Bfs\) 策略首先是正确的,代码:
#include<bits/stdc++.h>
using namespace std;
const int N=210;
const int inf=0x3f3f3f3f;
int n,m,s,t;
int fw[N][N],pre[N]; //残留网络,初始化为原图
bool vis[N];
queue<int> q;
bool bfs(int s,int t){//寻找一条从s到t的增广路,若找到返回true
memset(pre,0,sizeof pre);
memset(vis,0,sizeof vis);
while(q.size()) q.pop();
q.push(s),pre[s]=s,vis[s]=1;
while(q.size()){
int x=q.front();q.pop();
for(int i=1;i<=n;i++)
if(fw[x][i]>0&&!vis[i]){
pre[i]=x,vis[i]=1;
if(i==t) return 1;
q.push(i);
}
}
return 0;
}
int EdmondsKarp(int s,int t){
int flow=0,f;
while(bfs(s,t)){
f=inf;
for(int i=t;i!=s;i=pre[i])
f=min(f,fw[pre[i]][i]);
for(int i=t;i!=s;i=pre[i])
fw[pre[i]][i]-=f,fw[i][pre[i]]+=f;
flow+=f;
}
return flow;
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1,x,y,f;i<=m;i++){
scanf("%d%d%d",&x,&y,&f);
fw[x][y]+=f;
}
printf("%d\n",EdmondsKarp(s,t));
return 0;
}
\(EK\) 比较 \(Dinic\) 已经不抽象很多了,但为了方便理解,举以下图例:
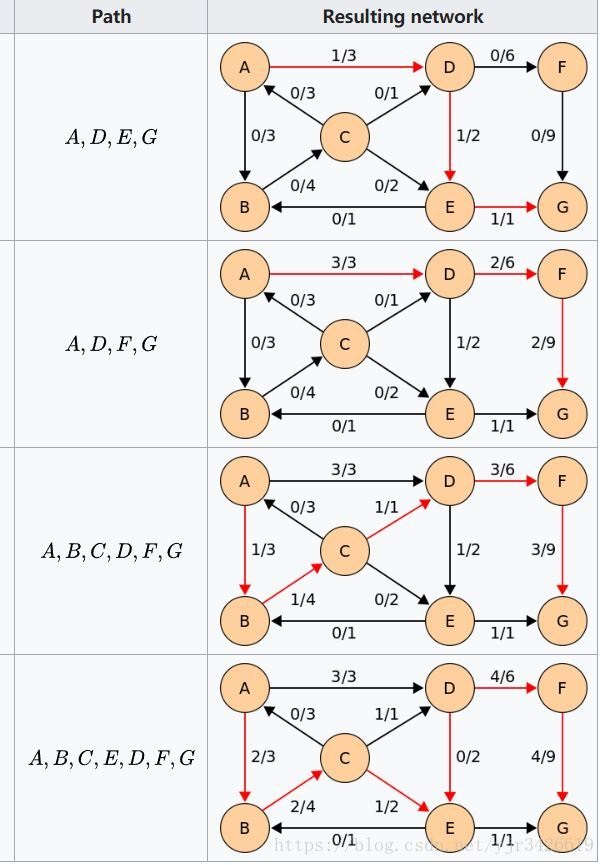
可以看出\(EK\)算法有很多多余的增广与遍历。《算法导论》中证明了在每次 \(Bfs\) 查找增广路之后,最短增广路的长度一定是非减的,也即对于每一个节点,它到源点的最短距离是非减的。 同时根据\(EK\)的增广过程,我们可以推导出在\(EK\)算法中所能找到的增广路的数量为 \(\Theta(VE)\)。由于 \(Bfs\) 找增广路的时间复杂度为 \(\Theta(E)\),而至多进行 \(\Theta(VE)\) 次查找,因此就可以得出\(EK\)算法的时间复杂度为 \(\Theta(VE^2)\)。
虽说 \(EK\) 算法是“时间换码量”,但当整个图是稀疏图的时候,使用\(EK\)算法不失为一种简便可行的方法,但是如果图的边数非常多,这个算法的性能也就显得不是那么优秀。
\(SAP\)算法是对\(Dinic\)算法一个小的优化。在\(Dinic\)算法中,每次增广都要进行一次\(Bfs\)来更新层次网络,这是一种浪费,因为有些点的层次实际上是不需要更新的。\(SAP\)算法就采取一边找增广路,一边更新层次网络的策略。代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
const int M=2e5+10;
const int inf=0x3f3f3f3f;
int n,m,s,t,fw[N][N]; //邻接矩阵
int dep[N],gap[N],pre[N]; //层次、gap优化、前驱
int SAP(int s,int t){
int flow=0,x=s,y,f;
gap[0]=n,pre[s]=s;
while(dep[s]<n){
for(y=1;y<=n;y++)
if(fw[x][y]&&dep[x]==dep[y]+1) break; //找增广边
if(y<=n){//找到了
pre[y]=x,x=y;
if(x==t){ //找到了一条增广路
f=inf;
for(int i=x;i!=s;i=pre[i])
f=min(f,fw[pre[i]][i]);
flow+=f;
for(int i=x;i!=s;i=pre[i])
fw[pre[i]][i]-=f,fw[i][pre[i]]+=f;
x=s; //同EK
}
} else {
f=inf;
for(int i=1;i<=n;i++)
if(fw[x][i]) f=min(f,dep[i]);
gap[dep[x]]--;
if(!gap[dep[x]]) break;
dep[x]=f+1,gap[dep[x]]++,x=pre[x]; //gap优化,使层次尽量小
}
}
return flow;
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1,x,y,f;i<=m;i++){
scanf("%d%d%d",&x,&y,&f);
fw[x][y]+=f;
}
printf("%d\n",SAP(s,t));
return 0;
}
在\(SAP\)算法中源点的层次是最高的。一定要有\(GAP\)优化,这个算法的时间复杂度优越性也得不到良好的表现。\(SAP\)算法的复杂度上界和\(Dinic\)一样也是 \(\Theta(V^2E)\)。
\(HLPP\)算法即最高标号预流推进算法。与前面三种算法不同的是,它并不采取找增广路的思想,而是不断地在可行流中找到那些仍旧有盈余的节点,将其盈余的流量推到周围可接纳流量的节点中。
对于一个最大流而言,除了源点和汇点以外所有的其他节点都应该满足流入的总流量等于流出的总流量,如果首先让源点的流量都尽可能都流到其相邻的节点中,这个时候相邻的节点就有了盈余,即它流入的流量比流出的流量多,所以要想办法将这些流量流出去。这种想法其实很自然,如果不知道最大流求解的任何一种算法,要手算最大流的时候,采取的策略肯定会是这样,将能流的先流出去,遇到容量不足的边就将流量减少,直到所有流量都流到了汇点。
但是这样做肯定会遇到一个问题,可能会有流量从一个节点流出去然后又流回到这个节点。如果这个节点是源点的话这么做是没问题的,因为有的时候通过某些节点是到达不了汇点的,这个时候要将流量流回到源点,但是其他情况就可能会造成循环流动,因此需要用到层次网络,只在相邻层次间流动。
#include <bits/stdc++.h>
using namespace std;
#define lng long long
#define fo(i,a,b,c) for(int i=a;i<=b;i+=c)
#define al(i,g,x) for(int i=g[x];i;i=e[i].nex)
const int V=2e3;
const int M=4e5;
const int inf=0x3f3f3f3f;
int n,m,s,t,p;
namespace graph{
class edge{
public:
int adj,nex,fw;
}e[M];
int g[V],top=1;
void add(int x,int y,int w){
e[++top]=edge{y,g[x],w},g[x]=top;
}
void Add(int x,int y,int w){
add(x,y,w),add(y,x,0);
}
}using namespace graph;
namespace HLPP{
int fl[V],dep[V],ct[V<<1]; //节点盈余、层次和gap优化
bool vis[V]; //访问
queue<int> Q;
class cmp{public:
bool operator()(int x,int y){return dep[x]<dep[y];}
};
priority_queue<int,vector<int>,cmp> q; //优先推进层次高的节点
bool bfs(){ //和Dinic差不多的bfs
fo(i,1,p,1) dep[i]=inf,vis[i]=0;
Q.push(t),dep[t]=0,vis[t]=1;
while(Q.size()){
int x=Q.front();Q.pop(),vis[x]=0;
al(i,g,x){ int to=e[i].adj;
if(e[i^1].fw&&dep[to]>dep[x]+1){
dep[to]=dep[x]+1;
if(!vis[to]) Q.push(to),vis[to]=1;
}
}
}
return dep[s]<inf;
}
void Push(int x){ //推x节点盈余的流
al(i,g,x){ int to=e[i].adj;
if(e[i].fw&&dep[to]+1==dep[x]){
int f=min(fl[x],e[i].fw);
e[i].fw-=f,e[i^1].fw+=f;
fl[x]-=f,fl[to]+=f;
if(!vis[to]&&to!=t&&to!=s)
q.push(to),vis[to]=1;
if(!fl[x]) break;
}
}
}
void Low(int x){ //gap优化,离散化层次
dep[x]=inf;
al(i,g,x){ int to=e[i].adj;
if(e[i].fw&&dep[x]>dep[to]+1)
dep[x]=dep[to]+1;
}
}
int hlpp(){
if(!bfs()) return 0;
dep[s]=p; //源点层次最高
fo(i,1,p,1)if(dep[i]<inf)
ct[dep[i]]++;
al(i,g,s){int to=e[i].adj,f; //先将源点推流
if((f=e[i].fw)>0){
e[i].fw-=f,e[i^1].fw+=f;
fl[s]-=f,fl[to]+=f;
if(to!=t&&to!=s&&!vis[to])
q.push(to),vis[to]=1;
}
}
while(q.size()){ //取层次大的节点预流推进
int x=q.top();q.pop(),vis[x]=0;
Push(x);
if(fl[x]){
if(!--ct[dep[x]]) //Gap优化
fo(to,1,p,1) if(to!=s&&to!=t
&&dep[to]>dep[x]&&dep[to]<=p)
dep[to]=p+1;
Low(x),ct[dep[x]]++;
q.push(x),vis[x]=1;
}
}
return fl[t];
}
}using namespace HLPP;
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t),p=n;
fo(i,1,m,1){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
Add(x,y,z);
}
printf("%d\n",hlpp());
return 0;
}
推进都是从高层次节点推到低层次节点中,源点的层次始终为节点总数。我们注意到预流推进算法的程序实现中有个优先队列,这使得程序会先取层次较高的节点推进。因为层次较低的节点是有可能接受到层次高节点流出的流量的,如果先推层次低的节点的流量,之后它有可能又接受到了高层次节点的流量,那么又要对其作推进处理。而如果每次都先将高层次节点取出,就可以将所有的高层次的节点的流量都先推入对应的低层次的节点中,在低层次的节点中先累积流量,最后再一起推进,提升效率。
特别的,\(HLPP\)算法的时间复杂度上限为 \(\Theta(V^2\sqrt E)\),所以有时\(HLPP\)过得了别的算法过不了的题。
如果某某 \(Tarjan\) 算法仅用于图上,那么这个算法的题就非常单调了。幸好后来有神仙发明了\(2-sat\)挽救了这个算法。
同理,如果网络流只能用来计算下水管道里的东西的话,那么它就不会风靡\(OI\)了。所以,蒟蒻在这里放几个经典例题,来跟大家具体讲解。
然后你有\(5\)分钟的读题时间和\(2\)分钟的惊讶时间。
你拿到这题后,会吃惊:这更像\(dp\)题一些!如果你学过二分图(匈牙利算法),你可能就会知道——这是两个连着的二分图。
你可以这么想,一组教辅就像一条 \(s\to\texttt{练习册}\to\texttt{书}\to\texttt{答案}\) 的路径。其中练习册和书得可能对应,书和答案也得可能对应。所以可以把书、练习册、答案先全扔地上,然后从源点向练习册连边,从答案向汇点连边,从练习册向可能对应的书连边,从书向可能对应的答案连边(流量都为\(1\),如下),就有 \(10\) 分了(???)。
你会再次惊讶:这么完美的图哪错了呢?其实你仔细看会发现:上面图的最大流为 \(2\),而你只能凑成 \(1\) 套教辅。
其中的玄机是:上面那本书被用了两次!可是你不能给点设流量啊,所以大技巧出场:拆点(如下)。
把每本书拆成两本,入边连一本,出边连一本,两本间流量为 \(1\),这样就相当于给点设了个流量,保证了一本书只用一遍。
整理一下:
\(s\xRightarrow{flow=1} \texttt{每本练习册}\)
\(\texttt{每本练答案}\xRightarrow{flow=1} t\)
对于每本书:
\(\texttt{该书左半本}\xRightarrow{flow=1} \texttt{该书右半本}\)
然后对于每个书和练习册的关系:
\(\texttt{该练习册}\xRightarrow{flow=1} \texttt{该书左半本}\)
然后对于每个书和答案的关系:
\(\texttt{该书右半本}\xRightarrow{flow=1}\texttt{该答案}\)
节点数\(=2N_1+N_2+N_3+2\le 40002\),边数\(=2(N_1+N_2+N_3+M_1+M_2)\le140000\)。代码:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
template<int V,int M>
class Dinic{
public:int E,g[V],to[M],nex[M],fw[M];
void clear(){memset(g,0,sizeof g),E=1;}
//E=1保证了互为反边的两条边可以通过^1互相得到
Dinic(){clear();}
//初始化
void add(int x,int y,int f){nex[++E]=g[x],to[E]=y,fw[E]=f,g[x]=E;}
//标准加边
void Add(int x,int y,int f){add(x,y,f),add(y,x,0);}
//加正边和反边,使得增广可以反悔
int dep[V],cur[V];bool vis[V];queue<int> q;
//dep表示层次,cur为单前弧优化,下面会讲。
//vis表示是否访问,queue维护bfs
bool bfs(int s,int t,int p){
for(int i=1;i<=p;i++) vis[i]=0,cur[i]=g[i];
q.push(s),vis[s]=1,dep[s]=0; //从源点开始bfs
while(q.size()){
int x=q.front();q.pop();
for(int i=g[x];i;i=nex[i])if(!vis[to[i]]&&fw[i])
q.push(to[i]),vis[to[i]]=1,dep[to[i]]=dep[x]+1;
//bfs过程中顺便给每个节点标上层次。
}
return vis[t]; //表示联通
}
int dfs(int x,int t,int F){
if(x==t||!F) return F;
int f,flow=0;
for(int&i=cur[x];i;i=nex[i]) //即i=g[x]
if(dep[to[i]]==dep[x]+1&&(f=dfs(to[i],t,min(F,fw[i])))>0) //沿着层次增广
{fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F) break;}
//边的流量调整
return flow; //一次增广的流量。
}
int dinic(int s,int t,int p){ //多次增广函数
int res=0,f;
while(bfs(s,t,p)) while((f=dfs(s,t,inf))) res+=f;
return res;
}
};
int n1,n2,n3,m1,m2,s,t,p;
Dinic<40010,140010> net;
int main(){
scanf("%d%d%d",&n1,&n2,&n3);
p=t=n1*2+n2+n3+2,s=t-1;
for(int i=1;i<=n2;i++)
net.Add(s,i+n1*2,1);
for(int i=1;i<=n3;i++)
net.Add(i+n1*2+n2,t,1);
for(int i=1;i<=n1;i++)
net.Add(i,i+n1,1);
scanf("%d",&m1);
for(int i=1,x,y;i<=m1;i++){
scanf("%d%d",&x,&y);
net.Add(y+n1*2,x,1);
}
scanf("%d",&m2);
for(int i=1,x,y;i<=m2;i++){
scanf("%d%d",&x,&y);
net.Add(x+n1,y+n1*2+n2,1);
}
printf("%d\n",net.dinic(s,t,p));
return 0;
}
总结:此题做法是拆点\(+\)最大流
你做完这道题后,想必对网络流的解题方法有了些了解,那么看下面这道例题:
然后你有\(5\)分钟的读题时间和\(2\)分钟的谔谔时间。
这题自己做估计能消耗一个下午,但这题是经典中的经典。假设你思考过了,我就开始讲题了:
我自己以前写的题解:题解 P3355 【骑士共存问题】
先将格图黑白间隔染色,由于一只骑士能攻击到的骑士在与自己异色的格中,有一种摆法是都摆白格子上或黑格子上。所以先将能放骑士的地方都放上,然后把扔掉最少骑士化为求最小割问题。
因为有矛盾的骑士只能放一个,所以先\(s\) 向每个白格点连流量为 \(1\) 的边,每个黑格点向 \(t\) 连流量为 \(1\) 的边,然后把一条互相攻击的关系变为网络流路径,流量为 \(\infty\),然后求最小割 。答案是总共能放的骑士数\(-\)网络流最小割。如下图:
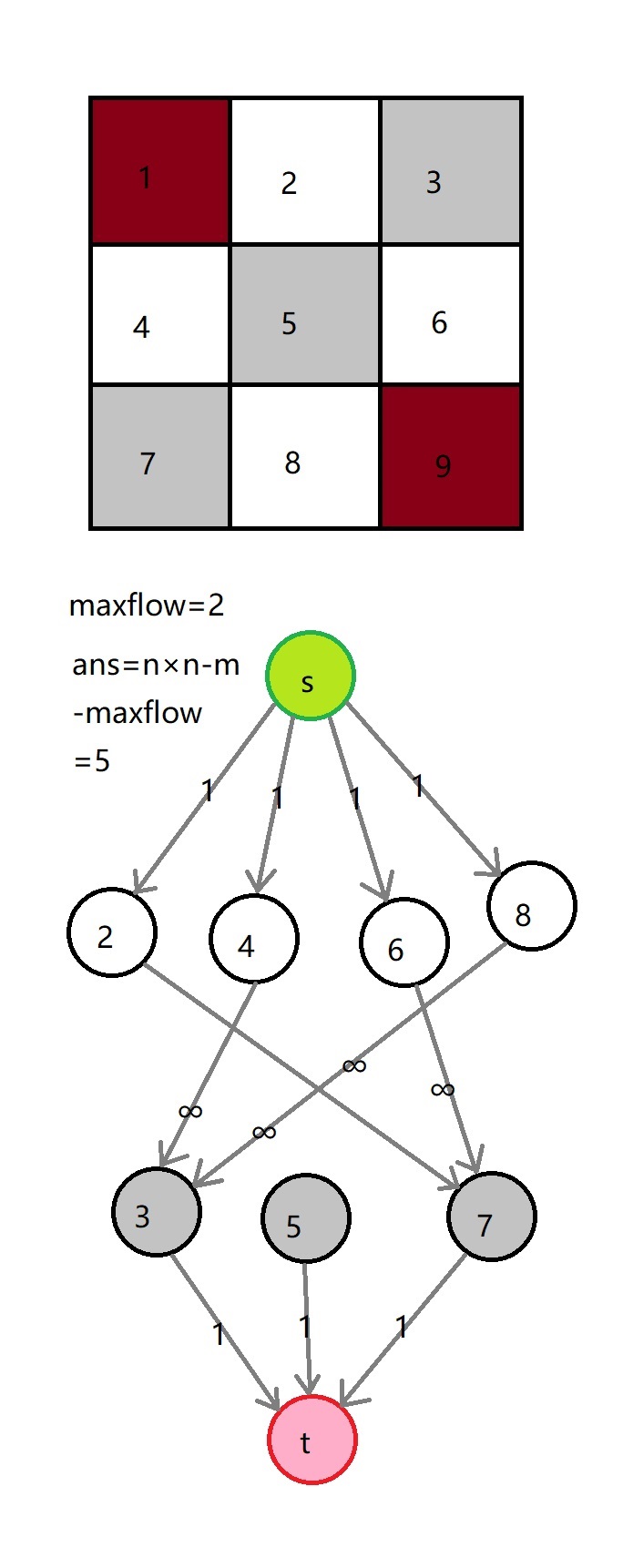
代码(以前写的,码风很蒻):
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+10; //n方大小
const int M=2e6+10; //10n方大小
const int inf=1e8+10;
int n,m,s,t,ans;
struct edge{
int adj,nex,fw;
}e[M];
int g[N],top=1;
void add(int x,int y,int z){
e[++top]=(edge){y,g[x],z};
g[x]=top;
}
//以下是最大流模板,每道题都一样
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool bfs(){
for(int i=1;i<=n;i++)
vis[i]=0,cur[i]=g[i];
Q.push(s),vis[s]=1,dep[s]=0;
while(Q.size()){
int x=Q.front(); Q.pop();
for(int i=g[x];i;i=e[i].nex){
int to=e[i].adj;
if(!vis[to]&&e[i].fw){
vis[to]=1;
dep[to]=dep[x]+1;
Q.push(to);
}
}
}
return vis[t];
}
int dfs(int x,int F){
if(!F||x==t)
return F;
int flow=0,f;
for(int i=cur[x];i;i=e[i].nex){
int to=e[i].adj; cur[x]=i;
if(dep[x]+1==dep[to]&&
(f=dfs(to,min(F,e[i].fw)))>0){
e[i].fw-=f;
e[i^1].fw+=f;
flow+=f,F-=f;
if(!F) break;
}
}
return flow;
}
int p(int x,int y){return (x-1)*n+y;} //给点编号
bool G[210][210]; //1表示障碍,0表示可放骑士
int tx[]={1,1,2,2,-1,-1,-2,-2};
int ty[]={-2,2,-1,1,-2,2,-1,1}; //攻击方向
int main(){
scanf("%d%d",&n,&m);
for(int i=1,x,y;i<=m;i++){
scanf("%d%d",&x,&y);
G[x][y]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(G[i][j]) continue;
if((i+j)&1){ //白格子
add(1,p(i,j)+1,1);
add(p(i,j)+1,1,0);
for(int k=0;k<8;k++){
int xt=tx[k]+i,yt=ty[k]+j;
if(xt<1||xt>n||yt<1||yt>n||G[xt][yt])
continue;
add(p(i,j)+1,p(xt,yt)+1,inf);
add(p(xt,yt)+1,p(i,j)+1,0);
}
} else add(p(i,j)+1,n*n+2,1), //黑格子
add(n*n+2,p(i,j)+1,0);
}
ans=n*n-m,s=1,n=t=n*n+2; //将ans初始化,将n变为网络流节点数
while(bfs()) ans-=dfs(s,inf); //网络流模板
printf("%d\n",ans);
return 0;
}
总结:做题要双向思考。这题中用到了要把求能放几个转化为最少扔几个,把最大流题转化为最小割。
最小割经典例题,简讲。
\(s\) 连每次拍照,流量为获益。每个下属连 \(t\),流量为交费。每次拍照连相关下属,流量为无穷。用最小割思想,要么牺牲收益,要么交费,答案为收益总和\(-\)网络流图最小割。
难度在于输出方案,需要掌握网络流的精髓。
只有你知道网络流每条边是什么意思,这题没有难点。蒟蒻就放一下输出方案部分的代码吧:
for(int i=1;i<=k;i++){
printf("%d:",i);
for(int j=g[i+tmp+1];j;j=e[j].nex){
int to=e[j].adj;
if(to>1&&to<=tmp+1&&e[j].fw)
printf(" %d",to-1);
}
puts("");
}
你现在有 \(5\) 分钟的看题时间和 \(2\) 分钟的谔谔时间。(我保证这题就是网络最大流题)[提示]
如果你实在做不出来,看了提示后可能恍然大悟。二分是个重要的思路,但这题怎么二分呢?首先这里的道路长度是不可以直接利用的,要 \(Floyd\) 求一下节点两两直接的最短路,然后二分时间,如果两个节点可以走到,连边(因为有初始结束状态,所以拆点),然后跑普通的最大流。
整理一下:
二分时间 \(midt\)。
\(s\) 向每个牛棚的一号点连流量为牛数的边
每个牛棚的二号点向 \(t\) 连流量为牛棚容量的边
对于每两个点 \(i,j\),如果 \(dis[i][j]\) 小于等于 \(midt\)(\(dis\) 是 \(Floyd\) 出来的最短路数组,\(dis[x][x]=0\)),就由 \(i\) 的一号点连向 \(j\) 的二号点,流量为 \(\infty\)。
如果最大流\(=\)总牛数,那么答案 \(\le midt\)。否则,答案 \(\ge midt\)。
蒟蒻的代码:
#include <bits/stdc++.h>
using namespace std;
#define lng long long
const int N=5e2;
const int M=1e5;
const lng R=1e12;
const lng inf=1e16;
int n,m,s,t;
lng res,ans,dis[N][N];
struct G{
struct edge{
int adj,nex;
lng fw;
}e[M];
int g[N],top;
G(){top=1;}
void add(int x,int y,lng z){
// printf("%d-%d %d\n",x,y,z);
e[++top]=(edge){y,g[x],z};
g[x]=top;
}
}O,D;
struct side{
int d; lng tim;
};
vector<side> es;
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool bfs(){
for(int i=1;i<=n;i++)
vis[i]=0,cur[i]=D.g[i];
Q.push(s),vis[s]=1,dep[s]=0;
while(Q.size()){
int x=Q.front(); Q.pop();
for(int i=D.g[x];i;i=D.e[i].nex){
int to=D.e[i].adj;
if(!vis[to]&&D.e[i].fw){
vis[to]=1;
dep[to]=dep[x]+1;
Q.push(to);
}
}
}
return vis[t];
}
lng dfs(int x,lng F){
if(!F||x==t)
return F;
lng flow=0,f;
for(int i=cur[x];i;i=D.e[i].nex){
int to=D.e[i].adj; cur[x]=i;
if(dep[x]+1==dep[to]&&
(f=dfs(to,min(F,D.e[i].fw)))>0){
D.e[i].fw-=f;
D.e[i^1].fw+=f;
flow+=f,F-=f;
if(!F) break;
}
}
return flow;
}
bool enough(lng T){
D=O,ans=0;
for(auto i:es)
if(i.tim>T)
D.e[i.d].fw=0;
while(bfs()) ans+=dfs(s,inf);
return ans>=res;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
lng x,y;
scanf("%lld%lld",&x,&y);
res+=x;
O.add(1,i+1,x);
O.add(i+1,1,0);
O.add(i+n+1,2*n+2,y);
O.add(2*n+2,i+n+1,0);
for(int j=1;j<=n;j++)
if(i!=j) dis[i][j]=inf;
}
for(int i=1,a,b;i<=m;i++){
lng c;
scanf("%d%d%lld",&a,&b,&c);
dis[a][b]=min(dis[a][b],c);
dis[b][a]=dis[a][b];
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=min(dis[i][j],
dis[i][k]+dis[k][j]);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
O.add(i+1,j+n+1,res);
es.push_back((side){O.top,dis[i][j]});
O.add(j+n+1,i+1,0);
}
}
s=1,n=t=2*n+2;
lng l=0,r=R+1;
while(l<r-1){
lng mid=(l+r)>>1;
if(enough(mid)) r=mid;
else l=mid;
}
if(r==R+1) puts("-1");
else printf("%lld\n",r);
return 0;
}
总结:想到了用二分就解决了题目的一半。
数据范围小得很,如果你觉得简单就谔谔吧。
这题是拆点的终极例题——时间拆点。因为太空船的运输是考时间组织的,所以把每个太空站(包括地月)拆成最大时间个点。同上题,二分时间来拆点。太空船就转化为不同太空站(包括地月)不同时间之间的边,同个太空站相邻时间之间连流量为 \(\infty\) 的边。
整理一下:
二分时间 \(midt\)
\(s\) 向地球的第 \(0\) 时间连流量为 \(k\) 的边。
每个太空站(包括地月)前一时间向后一时间连流量为 \(\infty\) 的边。
对于每个太空船的每一时刻,由它现在应该在的位置的该时间点节点向下一时间它应该在的位置的下一时间点节点连流量为太空船容量的边。
月球的第 \(midt\) 时间向 \(t\) 连流量为 \(k\) 的边。
如果最大流\(=k\),\(midt\) 减半;否则 \(midt\) 增半。
蒟蒻的代码:
//750s*15=10500
#include <bits/stdc++.h>
using namespace std;
const int V=10510;
const int M=6e4;
const int inf=1e8;
int n,m,k,s,t,p,fans,h[22],cnt[22],sp[22][16];
class Graph{
public:
int top,g[V],to[M],fw[M],nex[M];
void clear(){memset(g,0,sizeof g),fans=0,top=1;}
void add(int x,int y,int f){nex[++top]=g[x],to[top]=y,fw[top]=f,g[x]=top;}
void Add(int x,int y,int f){add(x,y,f),add(y,x,0);}
};
class Dinic:public Graph{
int dep[V],cur[V]; bool vis[V]; queue<int> q;
bool bfs(){
for(int i=1;i<=p;i++) vis[i]=0,cur[i]=g[i];
q.push(s),vis[s]=1,dep[s]=0;
while(q.size()){
int x=q.front();q.pop();
for(int i=g[x];i;i=nex[i])if(!vis[to[i]]&&fw[i])
q.push(to[i]),dep[to[i]]=dep[x]+1,vis[to[i]]=1;
}
return vis[t];
}
int dfs(int x,int F){
if(x==t||!F) return F;
int f,flow=0;
for(int&i=cur[x];i;i=nex[i])
if(dep[to[i]]==dep[x]+1&&(f=dfs(to[i],min(F,fw[i])))>0)
{fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F) break;}
return flow;
}
public:
void dinic(){while(bfs()) fans+=dfs(s,inf);}
}net;
bool check(int x){
p=t=(n+2)*(x+1)+2,s=t-1;
net.clear();
net.Add(s,(n+1-1)*(x+1)+1,k),net.Add((n+2-1)*(x+1)+x+1,t,k);
for(int i=1;i<=(n+2);i++)
for(int j=1;j<=x;j++)
net.Add((i-1)*(x+1)+j,(i-1)*(x+1)+j+1,inf);
for(int i=1;i<=m;i++){
for(int j=1;j<=x;j++){
int now=sp[i][(j-1)%cnt[i]+1],to=sp[i][(j+1-1)%cnt[i]+1];
// printf("%d->%d\n",now,to);
net.Add((now-1)*(x+1)+j,(to-1)*(x+1)+j+1,h[i]);
}
}
net.dinic();
return fans>=k;
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=m;i++){
scanf("%d%d",h+i,cnt+i);
for(int j=1;j<=cnt[i];j++){
scanf("%d",&sp[i][j]);
if(sp[i][j]==0) sp[i][j]=n+1;
if(sp[i][j]==-1) sp[i][j]=n+2;
}
}
int l=0,r=751;
while(l<r-1){
int mid=(l+r)>>1;
if(check(mid)) r=mid; else l=mid;
}
if(r==751) puts("0");
else printf("%d\n",r);
return 0;
}
总结:三维生物的思考不能被维度所限制。
讲完了网络最大流的解题,如果你去找个题库刷刷,你会发现网络最大流根本不能满足我们的解题需要。面对更为复杂的情况,需要这一篇的主角出场——网络费用流。
首先讲讲费用流图。这种网络流图每条边比普通的网络流图多一个限制,就是 \(cost\),表示这条边上每走过 \(1\) 流量就要付费 \(cost\)。 如下:
最小费用最大流(就是俗称的费用流),就是求在最大流的情况下的最小费用。如上图的最大流为 \(1\) ,当流量走 \(s\to1\to2\to t\) 时达到最小费用最大流,此时的费用为 \(3\)。
常见的算法是\(EK\)、\(Dinic\)和zkw费用流。有些时候我们需要的是最大费用最大流,只需要对代码稍作转化即可。
大部分同求最大流的\(EK\),算法框架长这样:
int bfs(){
//找到一条增广路
}
int EK(){
//对找到的增广路进行一系列处理
}
因为最大流的一条支流肯定是处处流量相等的,所以一条支流的费用就为 流量 \(f\times\)一路费用和。可以证明,如果把一条边的费用看作边的长度,不停找最短路增广最大流的费用是最小的。
实现: 把原来最大流\(EK\)的 \(Dfs\) 变成最短路算法(你可以写\(Dij+heap\)、\(Bell\)、\(Spfa\) 或 \(Spfa+SLF\)等),把原来的层次数组 \(dep[x]\) 表示 \(x\) 到源点的最短路(如果源点无法到达就为 \(\infty\))。判断源点和汇点是否连通,就看 \(dep[t]\) 是否小于 \(\infty\)。然后最短增广路的一路费用和就是 \(dep[t]\)。
\(EK\)费用流代码:
#include <bits/stdc++.h>
using namespace std;
const int N=5e3+10;
const int M=(5e4+10)*2;
const int inf=0x3f3f3f3f;
int n,m,s,t,p;
int E=1,g[N],nex[M],to[M],fw[M],co[M];
struct cf{int c,f;}ans;
void add(int x,int y,int f,int c){
nex[++E]=g[x],to[E]=y,fw[E]=f,co[E]=c,g[x]=E;
}
void Add(int x,int y,int f,int c){
add(x,y,f,c),add(y,x,0,-c);
//因为费用流反悔可以退钱,所以反悔边的费用为-c
}
int dep[N],pe[N],pv[N];
bool vis[N];
deque<int> q;
bool spfa(){
memset(dep,0x3f,sizeof dep);
memset(vis,0x00,sizeof vis);
q.push_back(s),vis[s]=1,dep[s]=0;
while(q.size()){
int x=q.front();q.pop_front(),vis[x]=0;
for(int i=g[x];i;i=nex[i])
if(fw[i]&&dep[to[i]]>dep[x]+co[i]){
dep[to[i]]=dep[x]+co[i];//最短路
pe[to[i]]=i,pv[to[i]]=x;
if(!vis[to[i]]){
vis[to[i]]=1;
if(q.size()&&dep[to[i]]<dep[q.front()])
q.push_front(to[i]);
else q.push_back(to[i]); //SLF优化
}
}
}
return dep[t]<inf; //判断是否找到增广路(s和t的联通)
}
cf mcmf(){ //EK模板
cf res=cf{0,0};int f;
while(spfa()){
f=inf;
for(int i=t;i!=s;i=pv[i])
f=min(f,fw[pe[i]]);
for(int i=t;i!=s;i=pv[i])
fw[pe[i]]-=f,fw[pe[i]^1]+=f;
res.c+=f*dep[t],res.f+=f;
}
return res;
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1,x,y,f,c;i<=m;i++){
scanf("%d%d%d%d",&x,&y,&f,&c);
Add(x,y,f,c);
}
ans=mcmf();
printf("%d %d\n",ans.f,ans.c);
return 0;
}
\(EK\)算法求费用流同样是时间换码量,适用于稀疏图。
同\(EK\)费用流,只是把该算法的最大流版本的\(Dfs\)变成最短路算法,然后把 \(dep[]\) 数组设为最大流数组。蒟蒻喜欢用\(Spfa+SLF\)最短路,因为又好写又快。
\(Dinic\) 费用流的代码:
#include <bits/stdc++.h>
using namespace std;
const int N=2e3+10;
const int M=2e6+10;
const int inf=1e8;
int d(){int x; scanf("%d",&x); return x;}
int n,m,p,s,t,a[N],fans,cans;
struct edge{
int adj,nex,fw,r;
}e[M];
int g[N],top=1;
void add(int x,int y,int z,int w){
e[++top]=(edge){y,g[x],z,w};
g[x]=top;
}
void Add(int x,int y,int z,int w){
// printf("%d-%d %d %d\n",x,y,z,w);
add(x,y,z,w),add(y,x,0,-w);
}
int dep[N],cur[N];
bool vis[N];
deque<int> Q;
bool spfa(){ //最短路
for(int i=1;i<=p;i++)
vis[i]=0,dep[i]=inf,cur[i]=g[i]; //单前弧优化
Q.push_back(s),vis[s]=1,dep[s]=0;
while(Q.size()){
int x=Q.front(); Q.pop_front();
vis[x]=0;
for(int i=g[x];i;i=e[i].nex){
int to=e[i].adj,d=e[i].r;
if(e[i].fw&&dep[to]>dep[x]+d){
dep[to]=dep[x]+d;
if(!vis[to]){
vis[to]=1;
if(Q.size()&&dep[to]<dep[Q.front()])
Q.push_front(to);
else Q.push_back(to); //SLF优化
}
}
}
}
return dep[t]<inf; //判断是否找到增广路(s和t的联通)
}
int dfs(int x,int F){//Dinic模板
if(!F||x==t)
return F;
int flow=0,f;
vis[x]=1;
for(int i=cur[x];i;i=e[i].nex){
int to=e[i].adj; cur[x]=i;
if(!vis[to]&&dep[x]+e[i].r==dep[to]&&
(f=dfs(to,min(F,e[i].fw)))>0){
e[i].fw-=f;
e[i^1].fw+=f;
flow+=f,F-=f;
if(!F){
vis[x]=0;
break;
}
}
}
return flow;
}
int main(){
n=d(),m=d(),p=t=2*n+2,s=t-1;
for(int i=1;i<=n;i++){
a[i]=d(); Add(i+n,t,1,0);
Add(s,i,1,0),Add(s,i+n,1,a[i]);
}
for(int i=1;i<=m;i++){
int x=d(),y=d(),z=d();
if(x>y) swap(x,y);
if(z<a[y]) Add(x,y+n,1,z);
}
while(spfa()){ //求费用流
int D=dfs(s,inf);
fans+=D,cans+=D*dep[t];
}
printf("%d\n",cans);
return 0;
}
普通\(Dinic\)费用流每一次增广都得\(Spfa\)一遍,浪费了时间。
因为发明者是神仙zkw,所以叫zkw费用流(就是zkw线段树那个zkw)。它是\(Dinic\)费用流的一个优化——倒着\(Spfa\),这样的话每次\(Dfs\)后并不会影响所有节点的层次(最短路),就可以一次\(Spfa\)后\(Dfs\)多次了。
zkw费用流的代码:
#include <bits/stdc++.h>
using namespace std;
const int V=1e6;
const int M=3e6;
const int inf=0x3f3f3f3f;
int n,m,s,t,p,fans,cans;
class Graph{
public:
int top,to[M<<1],fw[M<<1],ct[M<<1];
vector<int> g[V];
Graph(){top=1;}
void add(int x,int y,int f,int c){
g[x].push_back(++top);
to[top]=y,fw[top]=f,ct[top]=c;
}
void Add(int x,int y,int f,int c){
add(x,y,f,c),add(y,x,0,-c);
}
};
class zkwMCMF:public Graph{
public:
int dep[V]; bool vis[V];
deque<int> q;
bool spfa(){
for(int i=1;i<=p;i++) vis[i]=0,dep[i]=inf;
q.push_back(t),vis[t]=1,dep[t]=0; //倒着spfa
while(q.size()){
int x=q.front();q.pop_front(),vis[x]=0;
for(auto i:g[x])if(fw[i^1]&&dep[to[i]]>dep[x]-ct[i]){
dep[to[i]]=dep[x]-ct[i];
if(!vis[to[i]]){
vis[to[i]]=1;
if(q.size()&&dep[to[i]]<dep[q.front()])
q.push_front(to[i]);
else q.push_back(to[i]);
}
}
}
return dep[s]<inf;
}
int dfs(int x,int F){
vis[x]=1;
if(x==t||!F) return F;
int f,flow=0;
for(auto i:g[x])if(!vis[to[i]]&&fw[i]&&dep[x]-ct[i]
==dep[to[i]]&&(f=dfs(to[i],min(F,fw[i])))>0){
cans+=f*ct[i],fw[i]-=f,fw[i^1]+=f,flow+=f,F-=f;
if(!F) break;
}
return flow; //Dinic主体代码不变
}
void mcmf(){
while(spfa()){ //求费用流代码
vis[t]=1;
while(vis[t]){ //一次Spfa多次Dfs
for(int i=1;i<=p;i++) vis[i]=0;
fans+=dfs(s,inf);
}
}
}
}network;
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t),p=n;
for(int i=1,x,y,f,c;i<=m;i++){
scanf("%d%d%d%d",&x,&y,&f,&c);
network.Add(x,y,f,c);
}
network.mcmf();
printf("%d %d\n",fans,cans);
return 0;
}
优点:很快,比\(EK\)快 \(4\) 倍。
\(\texttt{EK:}\color{orange}\texttt{1.76s}\)
\(\texttt{zkw费用流:}\color{#44cc44}\texttt{520ms}\)
费用流的解题套路和最大流差不多,无非就是多加了个费用条件。因为费用流的算法时间复杂度很玄学,所以有些时候优化很重要。
普通的费用流题目,只需要按图索骥即可。
同最大流解题思路,源点表示发货商,汇点表示该公司的客户。每个月都可以买无穷产品,所以 \(s\) 向每个月节点连流量为 \(\infty\) 费用为 \(d_i\) 的边;每个月节点向 \(t\) 连流量为 \(U_i\) 的边(满足最大流就相当于满足客户),因为每个月还可以储存,所以每个月节点向下个月节点(如果有下个月节点)连流量为 \(S\) 费用为 \(m\) 的边。 跑个最小费用最大流,总费用就是最低成本。
整理一下:
\(Dinic\)费用流代码(以前写的,码风很蒻):
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
const int M=6e6+10;
const int inf=1e8+10;
int n,m,S,s,t,fans,cosans;
struct edge{
int adj,nex,fw,r;
}e[M];
int g[N],top=1;
void add(int x,int y,int z,int w){
e[++top]=(edge){y,g[x],z,w};
g[x]=top;
}
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool spfa(){
// puts("spfa()");
for(int i=1;i<=n;i++)
vis[i]=0,dep[i]=inf;
Q.push(s),vis[s]=1,dep[s]=0;
for(int i=1;i<=n;cur[i]=g[i],i++);
while(Q.size()){
int x=Q.front(); Q.pop();
vis[x]=0;
for(int i=g[x];i;i=e[i].nex){
int to=e[i].adj,d=e[i].r;
if(e[i].fw&&dep[to]>dep[x]+d){
dep[to]=dep[x]+d;
if(!vis[to]){
vis[to]=1;
Q.push(to);
}
}
}
}
return dep[t]!=inf;
}
int dfs(int x,int F){
// puts("dfs");
if(!F||x==t)
return F;
int flow=0,f;
vis[x]=1;
for(int i=cur[x];i;i=e[i].nex){
int to=e[i].adj; cur[x]=i;
if(!vis[to]&&dep[x]+e[i].r==dep[to]&&
(f=dfs(to,min(F,e[i].fw)))>0){
e[i].fw-=f;
e[i^1].fw+=f;
flow+=f,F-=f;
if(!F){
vis[x]=0;
break;
}
}
}
return flow;
}
int main(){
scanf("%d%d%d",&n,&m,&S);
for(int i=1,x;i<=n;i++){
scanf("%d",&x);
add(i+1,n+2,x,0);
add(n+2,i+1,0,0);
}
for(int i=1,x;i<=n;i++){
scanf("%d",&x);
add(1,i+1,inf,x);
add(i+1,1,0,-x);
}
for(int i=1;i<n;i++)
add(i+1,i+2,S,m),
add(i+2,i+1,0,-m);
s=1; n=t=n+2;
while(spfa()){
int d=dfs(s,inf);
fans+=d,cosans+=d*dep[t];
}
printf("%d\n",cosans);
return 0;
}
总结:普通费用流题按图索骥即可。
思维难度排名前 \(10\%\),蒟蒻以前写的题解:传送门
我把这题的思想叫做接力棒思想,因为我就是想到接力棒的时候突然知道怎么做的。这题你想一个流遍历所有点是不可能的,因为这道题正好否决了所以这样的方法。
正解就像在接力跑。想象有 \(n+1\) 个人接力跑 ,刚开始时都在 \(s\) 点上,分别对应 \(s\) 和 \(1\sim n\) 这 \(n+1\) 个节点,开始时接力棒在 \(s\) 那个人手上。
\(1\sim n\) 算操场里的点,开始时 \(s\) 对应的运动员开跑。在未经召唤的情况下从场外到场内节点 \(i\) 需要花费 \(a_i\),所以 \(s\) 运动员就花费某个 \(a_x\) 到场内节点 \(x\),然后到达节点后打卡,休息。
然后 \(x\) 节点对应的运动员受到 \(s\) 的召唤,免费瞬移到 \(x\) 节点,然后沿着道路花费相应的费用到另一个节点,并打卡,休息,召唤该节点对应的运动员。
然后反复这个过程,除了 \(s\) 节点对应的运动员,别的运动员也可以花费 \(a_i\) 的费用跑到场内,或免费受召唤瞬移,最终所有 \(1\sim n\) 节点被打卡一次后,接力赛结束。
然后按照被转化的问题,按图索骥一下建个图,最后的最大流最小费用就是答案。
整理一下:
注1:这个图表示样例 \(1\) 的连边方法。
注2:题目中说只能星际航行到引力大的星球。
注3:图中的边流量都为 \(1\)。
\(\color{#7d0}\texttt{AC}\) 代码:
#include <bits/stdc++.h>
using namespace std;
const int N=2e3+10;
const int M=2e6+10;
const int inf=1e8;
int d(){int x; scanf("%d",&x); return x;}
int n,m,p,s,t,a[N],fans,cans;
struct edge{
int adj,nex,fw,r;
}e[M];
int g[N],top=1;
void add(int x,int y,int z,int w){
e[++top]=(edge){y,g[x],z,w};
g[x]=top;
}
void Add(int x,int y,int z,int w){
// printf("%d-%d %d %d\n",x,y,z,w);
add(x,y,z,w),add(y,x,0,-w);
}
int dep[N],cur[N];
bool vis[N];
queue<int> Q;
bool spfa(){
for(int i=1;i<=p;i++)
vis[i]=0,dep[i]=inf,cur[i]=g[i];
Q.push(s),vis[s]=1,dep[s]=0;
while(Q.size()){
int x=Q.front(); Q.pop();
vis[x]=0;
for(int i=g[x];i;i=e[i].nex){
int to=e[i].adj,d=e[i].r;
if(e[i].fw&&dep[to]>dep[x]+d){
dep[to]=dep[x]+d;
if(!vis[to]){
vis[to]=1;
Q.push(to);
}
}
}
}
return dep[t]!=inf;
}
int dfs(int x,int F){
if(!F||x==t)
return F;
int flow=0,f;
vis[x]=1;
for(int i=cur[x];i;i=e[i].nex){
int to=e[i].adj; cur[x]=i;
if(!vis[to]&&dep[x]+e[i].r==dep[to]&&
(f=dfs(to,min(F,e[i].fw)))>0){
e[i].fw-=f;
e[i^1].fw+=f;
flow+=f,F-=f;
if(!F){
vis[x]=0;
break;
}
}
}
return flow;
}
int main(){
n=d(),m=d(),p=t=2*n+2,s=t-1;
for(int i=1,x;i<=n;i++){
a[i]=d(); Add(i+n,t,1,0);
Add(s,i,1,0),Add(s,i+n,1,a[i]);
}
for(int i=1;i<=m;i++){
int x=d(),y=d(),z=d();
if(x>y) swap(x,y);
if(z<a[y]) Add(x,y+n,1,z);
}
while(spfa()){
int D=dfs(s,inf);
fans+=D,cans+=D*dep[t];
}
printf("%d\n",cans);
return 0;
}
总结:网络流题一定、一定、一定要多思考。
本蒟蒻做过的最巧妙的费用流题目(没有之一),很谔谔。
源点连志愿者,志愿者连控制的天(区间),天连汇点是最典型的爆〇方式。这题的思想有点像有些比较抠的差分约束题的思想但又不是。
正解就像在闯关。每一天就是一关,开始时你有 \(\infty\) 个小人,到第 \(n+1\) 关时还有这么多小人,就赢了。 第 \(i\) 天只能免费通过 \(\infty-a_i\) (注:这里的 \(\infty\) 是有数值的,\(\infty\neq\infty-a_i\))个人,剩下的人需要乘坐不免费的时空穿越机。
每个志愿者就是一台能从 \(s_i\) 关跳到 \(t_i+1\) 关的时空穿越机,花费为 \(c_i\),只能乘坐一个小人。 但因为每种志愿者有无限个,所以可以看作能乘坐无穷小人,费用为 \(c_i/\)人。
求最后赢得所有 \(n+1\) 关最少的费用。然后按图索骥建个图,跑个最大流最小费用就是答案。
整理一下:
注:图为题目样例。
\(\color{#499}\texttt{AC}\) 代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
const int M=1e4+10;
const int P=2e4+10;
const int E=3e7+10;
const int inf=1e8;
int d(){int x;scanf("%d",&x);return x;}
int n,m,p,s,t,fans,cans;
struct edge{
int adj,nex,fw,r;
}e[E];
int g[P],top=1;
void add(int x,int y,int w,int r){
e[++top]=(edge){y,g[x],w,r};
g[x]=top;
}
void Add(int x,int y,int w,int r){
add(x,y,w,r),add(y,x,0,-r);
}
int dep[P],cur[P];
bool vis[P];
queue<int> q;
bool spfa(){
for(int i=1;i<=p;i++)
vis[i]=0,dep[i]=inf,cur[i]=g[i];
q.push(s),vis[s]=1,dep[s]=0;
while(q.size()){
int x=q.front();q.pop(),vis[x]=0;
for(int i=g[x];i;i=e[i].nex){
int to=e[i].adj,d=e[i].r;
if(e[i].fw&&dep[to]>dep[x]+d){
dep[to]=dep[x]+d;
if(!vis[to]) vis[to]=1,q.push(to);
}
}
}
return dep[t]!=inf;
}
int dfs(int x,int F){
if(!F||x==t)
return F;
int flow=0,f;
vis[x]=1;
for(int i=cur[x];i;i=e[i].nex){
int to=e[i].adj; cur[x]=i;
if(!vis[to]&&dep[x]+e[i].r==dep[to]
&&(f=dfs(to,min(F,e[i].fw)))>0){
e[i].fw-=f,e[i^1].fw+=f;
flow+=f,F-=f;
if(!F){vis[x]=0; break;}
}
}
return flow;
}
int main(){
n=d(),m=d();
p=t=n+m+3,s=t-1;
for(int i=1;i<=n;i++)
Add(i,i+1,inf-d(),0);
for(int i=1;i<=m;i++){
int S=d(),T=d(),C=d();
Add(S,T+1,inf,C);
}
Add(s,1,inf,0),Add(n+1,t,inf,0);
while(spfa()){
int D=dfs(s,inf);
fans+=D;
cans+=dep[t]*D;
}
printf("%d\n",cans);
}
总结:有什么好总结的呢,脑洞和思考最重要吧。
普通的网络流(包括最大流和费用流)的边只有最大流量限制,默认最小流量限制为 \(0\),但是你有没有想过最小流量限制不为 \(0\) 的网络最大流或网络费或可行流(满足限制的流)用流怎么做呢?
网络流图中没有源点和汇点,每条边 \(i\) 的流量都被限制在区间 \([L_i,R_i]\)中,问该网络中达到可行流量时每条边的流量(找一个方案)。模板:传送门。
对于第 \(i\) 条边 \((u,v)\),因为其流量区间大小为 \(R_i-L_i+1\),正好等于普通网络流流量为 \(R_i-L_i\) 时的区间大小,所以在网络流图中先连 \((u,v)\),流量为 \(R_i-L_i\) 以限制这条边的流量变化区间。
如果每个 \(L_i=0\),那么这样就已经对了。可是因为网络流需要满足每个节点的流入流量等于流出流量,所以记录 \(d[x]=\sum\limits _{i\in\{x‘s~inedge\}}L_i-\sum\limits_{i\in\{x‘s~outedge\}}L_i\) 。然后建立超级源点 \(S\) 和超级汇点 \(T\)。如果 \(d[x]>0\),就连 \((S,x)\),流量为 \(d[x]\);如果 \(d[x]<0\),就连 \((x,T)\),流量为 \(-d[x]\)。这样就起到了一个补流的作用,\(x\) 节点于是就这么流量守恒了。
同时,记录 \(sum=\sum\limits_{x\in node\&\&d[x]>0}d[x]\),
如果上面的网络流图跑出来的最大流 \(\neq sum\),说明不存在可行流。否则,原图(不包括补流边)每条边 \(i\) 在可行流中的流量可以是 \(fw[x\oplus 1]+L_i\),其中 \(fw[x\oplus 1]\) 表示这条边在最大流运行后实际流了的流量。
整理一下:
原图:
转化后图:
答案可行流:
代码:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
template<int V,int M>
class Dinic{
public:int E,g[V],to[M],nex[M],fw[M];
void clear(){memset(g,0,sizeof g),E=1;}
Dinic(){clear();}
void add(int x,int y,int f){nex[++E]=g[x],to[E]=y,fw[E]=f,g[x]=E;}
void Add(int x,int y,int f){add(x,y,f),add(y,x,0);}
int dep[V],cur[V];bool vis[V];queue<int> q;
bool bfs(int s,int t,int p){
for(int i=1;i<=p;i++) vis[i]=0,cur[i]=g[i];
q.push(s),vis[s]=1,dep[s]=0;
while(q.size()){
int x=q.front();q.pop();
for(int i=g[x];i;i=nex[i])if(!vis[to[i]]&&fw[i])
q.push(to[i]),vis[to[i]]=1,dep[to[i]]=dep[x]+1;
}
return vis[t];
}
int dfs(int x,int t,int F){
if(x==t||!F) return F;
int f,flow=0;
for(int&i=cur[x];i;i=nex[i])
if(dep[to[i]]==dep[x]+1&&(f=dfs(to[i],t,min(F,fw[i])))>0)
{fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F) break;}
return flow;
}
int dinic(int s,int t,int p){
int res=0,f;
while(bfs(s,t,p)) while((f=dfs(s,t,inf))) res+=f;
return res;
}
};
int n,m,s,t,p,d[210],sum,low[40010];
vector<int> oedge;
Dinic<220,40010> net;
int main(){
scanf("%d%d",&n,&m);
p=t=n+2,s=t-1;
for(int i=1,x,y,l,r;i<=m;i++){
scanf("%d%d%d%d",&x,&y,&l,&r);
net.Add(x,y,r-l);
d[x]-=l,d[y]+=l;
low[net.E]=l;
oedge.push_back(net.E);
}
for(int i=1;i<=n;i++)
if(d[i]>0) net.Add(s,i,d[i]),sum+=d[i];
else if(d[i]<0) net.Add(i,t,-d[i]);
if(net.dinic(s,t,p)!=sum) return puts("NO"),0;
else {
puts("YES");
for(auto i:oedge)
printf("%d\n",net.fw[i]+low[i]);
}
return 0;
}
总结:比较偏理论吧。
网络流图中有源点 \(s\) 和汇点 \(t\),每条边 \(i\) 的流量都被限制在区间 \([Li,Ri]\) 中,问该网络中达到可行流量时每条边的流量以及 \(s\) 到 \(t\) 的流量。
如果连 \((t,s)\) 流量为 \(\infty\),就转化成了无源汇上下界可行流问题,然后增加超级源汇补流边,解法同上,代码同上。
网络流图中有源点 \(s\) 和汇点 \(t\),每条边 \(i\) 的流量都被限制在区间 \([Li,Ri]\) 中,问该网络中达到可行最大流量时每条边的流量以及 \(s\) 到 \(t\) 的流量。
先跑一遍有源汇上下界可行流。如果可行,就用残余跑一次最大流,然后两个结果相加就是有源汇上下界最大流。解法同上,代码同上。
真的不是在敷衍你,就是这样的!
比较复杂。先建超级源点 \(S\),超级汇点 \(T\),然后按照规则连补流边,对 \(S\to T\) 跑一次最大流。然后对原图连一条 \((t,s)\) 的流量为 \(\infty\) 的边,然后再在残余网络上跑一次 \(S\to T\) 的最大流。然后答案就是最后加的 \((t,s)\) 边实际流的流量。 模板:传送门。
原理就是先跑个可行流然后不停缩减流量。
为了更好理解,放个代码:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
template<int V,int M>
class Dinic{
public:int E,g[V],to[M],nex[M],fw[M];
void clear(){memset(g,0,sizeof g),E=1;}
Dinic(){clear();}
void add(int x,int y,int f){nex[++E]=g[x],to[E]=y,fw[E]=f,g[x]=E;}
void Add(int x,int y,int f){add(x,y,f),add(y,x,0);}
int dep[V],cur[V];bool vis[V];queue<int> q;
bool bfs(int s,int t,int p){
for(int i=1;i<=p;i++) vis[i]=0,cur[i]=g[i];
q.push(s),vis[s]=1,dep[s]=0;
while(q.size()){
int x=q.front();q.pop();
for(int i=g[x];i;i=nex[i])if(!vis[to[i]]&&fw[i])
q.push(to[i]),vis[to[i]]=1,dep[to[i]]=dep[x]+1;
}
return vis[t];
}
int dfs(int x,int t,int F){
if(x==t||!F) return F;
int f,flow=0;
for(int&i=cur[x];i;i=nex[i])
if(dep[to[i]]==dep[x]+1&&(f=dfs(to[i],t,min(F,fw[i])))>0)
{fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F) break;}
return flow;
}
int dinic(int s,int t,int p){
int res=0,f;
while(bfs(s,t,p)) while((f=dfs(s,t,inf))) res+=f;
return res;
}
};
const int N=6e4+10;
const int M=5e5+10;
int n,m,s,t,S,T,p,d[N],sum,ans;
Dinic<N,M> net;
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
p=T=n+2,S=T-1;
for(int i=1,x,y,l,r;i<=m;i++){
scanf("%d%d%d%d",&x,&y,&l,&r);
net.Add(x,y,r-l);
d[x]-=l,d[y]+=l;
}
for(int i=1;i<=n;i++)
if(d[i]>0) net.Add(S,i,d[i]),sum+=d[i];
else if(d[i]<0) net.Add(i,T,-d[i]);
ans+=net.dinic(S,T,p); //三行核心代码
net.Add(t,s,inf); //三行核心代码
ans+=net.dinic(S,T,p); //三行核心代码
if(ans!=sum) puts("please go home to sleep");
else printf("%d\n",net.fw[net.E]);
return 0;
}
闭合图是在一个图中,选取一些点构成点集,若集合中任意点连接的出边所通往的点也在该点集中,则这个点集以及所有这些边构成闭合图。最大权闭合子图即点权之和最大的闭合图。
要求一个图的最大权闭合子图,先建立源点 \(s\) 和汇点 \(t\)。然后连 \((s,\) 正权点\()\),流量为点的权值;连 \((\)负权点\(,t)\) ,流量为点权的相反数。点与点之间按照边原来的方向连流量为 \(\infty\) 的边。
然后该图的最大权闭合子图就为 \((\)正权点权值之和\(-\)网络流图最大流\()\)。
该算法其实题目较少,属于冷门算法。但蒟蒻找了很久还是找到了一道好例题。
看了题目,你会谔谔道:这是有上下界的费用流!你是对的,如果你掌握了有上下界的最大流,也就掌握了有上下界的费用流。
对于像有上下界的网络流这样的偏理论性算法,应该做到触类旁通,这题虽然是“有上下界的费用流”,但和有上下界的最大流本质是一样的。
很明显,为了先构建一个有上下界的网络最大流模型,要增加汇点 \(t‘\)(因为 \(t\) 是题面中的变量,所以不能用),使所有不是树根节点的节点可以连到 \(t‘\),流量范围 \([0,\infty]\),费用 \(0\),以确保看完剧情。然后对于每条树上边,看作流量下限为 \(1\) 上限为 \(\infty\) ,费用为 \(t_{i,j}\) 的费用流边。
然后按照解决有有源汇有上下界的网络可行流的方法,跑个最小费用可行流就好了。代码如下:
#include <bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
template<int V,int M>
class zkwmcmf{
public:int E,g[V],to[M],nex[M],fw[M],ct[M],fans,cans;
void clear(){memset(g,0,sizeof g),E=1,fans=cans=0;}
zkwmcmf(){clear();}
void add(int x,int y,int f,int c){
nex[++E]=g[x],to[E]=y,fw[E]=f,ct[E]=c,g[x]=E;
}
void Add(int x,int y,int f,int c){add(x,y,f,c),add(y,x,0,-c);}
int dep[V];bool vis[V];deque<int> q;
bool spfa(int s,int t,int p){
for(int i=1;i<=p;i++) vis[i]=0,dep[i]=inf;
q.push_back(t),dep[t]=0,vis[t]=1;
while(q.size()){
int x=q.front();q.pop_front(),vis[x]=0;
for(int i=g[x];i;i=nex[i])
if(fw[i^1]&&dep[to[i]]>dep[x]-ct[i]){
dep[to[i]]=dep[x]-ct[i];
if(!vis[to[i]]){
vis[to[i]]=1;
if(q.size()&&dep[to[i]]<dep[q.front()])
q.push_front(to[i]);
else q.push_back(to[i]);
}
}
}
return dep[s]<inf;
}
int dfs(int x,int t,int F){
vis[x]=1;
if(x==t||!F) return F;
int f,flow=0;
for(int i=g[x];i;i=nex[i])if(fw[i]&&!vis[to[i]]&&
dep[to[i]]==dep[x]-ct[i]&&(f=dfs(to[i],t,min(F,fw[i])))>0)
{cans+=ct[i]*f,fw[i]-=f,fw[i^1]+=f,F-=f,flow+=f;if(!F)break;}
return flow;
}
void mcmf(int s,int t,int p){
while(spfa(s,t,p)){
vis[t]=1;
while(vis[t]){
memset(vis,0,sizeof vis);
fans+=dfs(s,t,inf);
}
}
}
};
int n,ans,d[510],s,t,p;
zkwmcmf<510,100010> net;
int main(){
scanf("%d",&n);
p=t=n+3,s=t-1;
for(int i=1,x,y,z;i<=n;i++){
scanf("%d",&x);
for(int j=1;j<=x;j++){
scanf("%d%d",&y,&z);
d[i]-=1,d[y]+=1,ans+=z;
net.Add(i,y,inf,z);
}
}
for(int i=2;i<=n;i++) net.Add(i,n+1,inf,0);
for(int i=1;i<=n;i++){
if(d[i]>0) net.Add(s,i,d[i],0);
if(d[i]<0) net.Add(i,t,-d[i],0);
}
net.Add(n+1,1,inf,0);
//代码其实就是一模一样的,费用流,最大流,到头来还是同个东西
net.mcmf(s,t,p);
printf("%d\n",net.cans+ans);
return 0;
}
然后我就讲到这里了,网络流的习题luogu上很多。网络流的知识其实还有 \(GHT\) 最小割树,但这么深奥的东西就不适合加入这篇文章了。文章有点长,看完的人都是赢家。这篇文章的图 \(70\%\) 是手画的,代码都是自己敲的,文字都是自己写的,略有借鉴巨佬博文。如果你喜欢我写的文章,就多点几个赞吧。
最后安利一下 \(\texttt{blog}\),祝大家学习愉快!
标签:vector 宽度 简单 多少 难度 地方 img 无法 bool
原文地址:https://www.cnblogs.com/Wendigo/p/12813027.html